Convection-Diffusion Equation: A Theoretically Certified Framework for Neural Networks
Paper and Code
Mar 23, 2024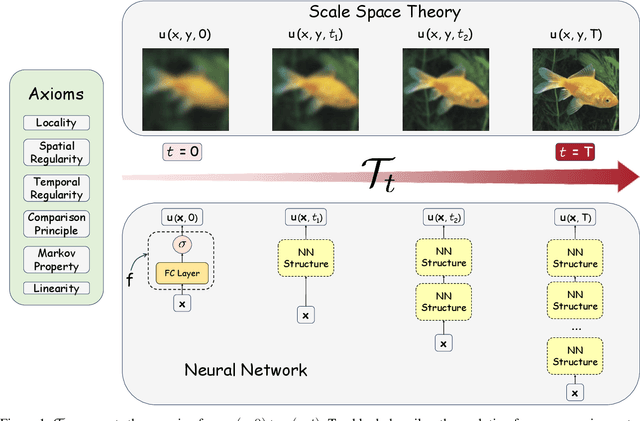
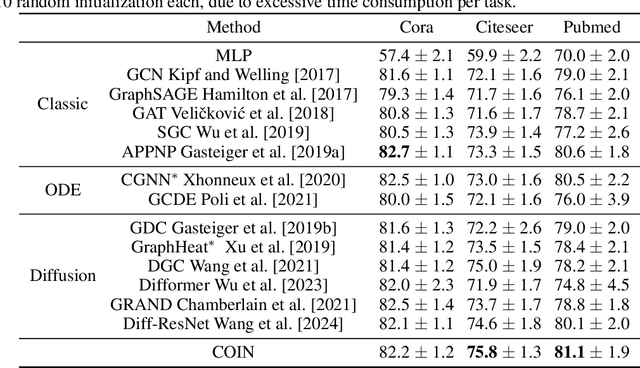
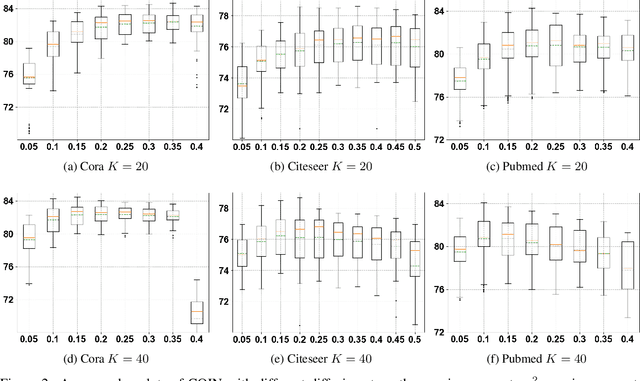

In this paper, we study the partial differential equation models of neural networks. Neural network can be viewed as a map from a simple base model to a complicate function. Based on solid analysis, we show that this map can be formulated by a convection-diffusion equation. This theoretically certified framework gives mathematical foundation and more understanding of neural networks. Moreover, based on the convection-diffusion equation model, we design a novel network structure, which incorporates diffusion mechanism into network architecture. Extensive experiments on both benchmark datasets and real-world applications validate the performance of the proposed model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge