Neumann Series-based Neural Operator for Solving Inverse Medium Problem

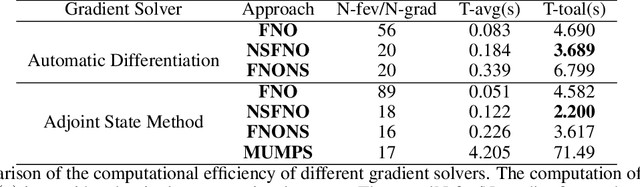
The inverse medium problem, inherently ill-posed and nonlinear, presents significant computational challenges. This study introduces a novel approach by integrating a Neumann series structure within a neural network framework to effectively handle multiparameter inputs. Experiments demonstrate that our methodology not only accelerates computations but also significantly enhances generalization performance, even with varying scattering properties and noisy data. The robustness and adaptability of our framework provide crucial insights and methodologies, extending its applicability to a broad spectrum of scattering problems. These advancements mark a significant step forward in the field, offering a scalable solution to traditionally complex inverse problems.

BI-GreenNet: Learning Green's functions by boundary integral network

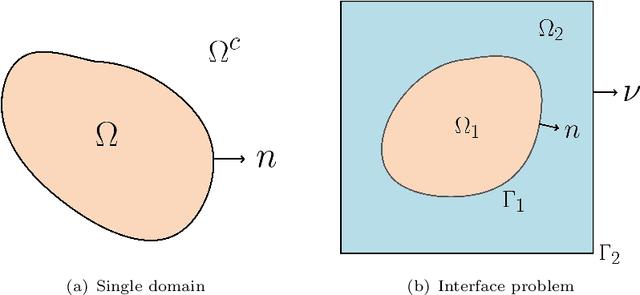
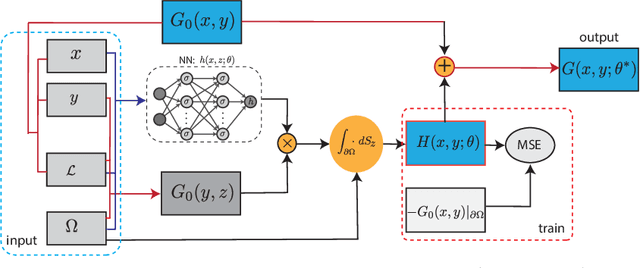
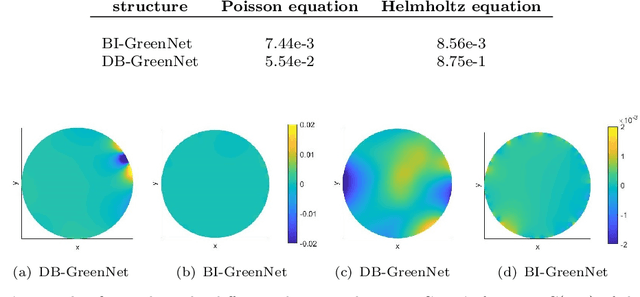
Green's function plays a significant role in both theoretical analysis and numerical computing of partial differential equations (PDEs). However, in most cases, Green's function is difficult to compute. The troubles arise in the following three folds. Firstly, compared with the original PDE, the dimension of Green's function is doubled, making it impossible to be handled by traditional mesh-based methods. Secondly, Green's function usually contains singularities which increase the difficulty to get a good approximation. Lastly, the computational domain may be very complex or even unbounded. To override these problems, we leverage the fundamental solution, boundary integral method and neural networks to develop a new method for computing Green's function with high accuracy in this paper. We focus on Green's function of Poisson and Helmholtz equations in bounded domains, unbounded domains. We also consider Poisson equation and Helmholtz domains with interfaces. Extensive numerical experiments illustrate the efficiency and the accuracy of our method for solving Green's function. In addition, we also use the Green's function calculated by our method to solve a class of PDE, and also obtain high-precision solutions, which shows the good generalization ability of our method on solving PDEs.