Decoding-Time Language Model Alignment with Multiple Objectives

Aligning language models (LMs) to human preferences has emerged as a critical pursuit, enabling these models to better serve diverse user needs. Existing methods primarily focus on optimizing LMs for a single reward function, limiting their adaptability to varied objectives. Here, we propose $\textbf{multi-objective decoding (MOD)}$, a decoding-time algorithm that outputs the next token from a linear combination of predictions of all base models, for any given weightings over different objectives. We exploit a common form among a family of $f$-divergence regularized alignment approaches (such as PPO, DPO, and their variants) to identify a closed-form solution by Legendre transform, and derive an efficient decoding strategy. Theoretically, we show why existing approaches can be sub-optimal even in natural settings and obtain optimality guarantees for our method. Empirical results demonstrate the effectiveness of the algorithm. For example, compared to a parameter-merging baseline, MOD achieves 12.8% overall reward improvement when equally optimizing towards $3$ objectives. Moreover, we experiment with MOD on combining three fully-finetuned LLMs of different model sizes, each aimed at different objectives such as safety, coding, and general user preference. Unlike traditional methods that require careful curation of a mixture of datasets to achieve comprehensive improvement, we can quickly experiment with preference weightings using MOD to find the best combination of models. Our best combination reduces toxicity on Toxigen to nearly 0% and achieves 7.9--33.3% improvement across other three metrics ($\textit{i.e.}$, Codex@1, GSM-COT, BBH-COT).

JoMA: Demystifying Multilayer Transformers via JOint Dynamics of MLP and Attention

We propose Joint MLP/Attention (JoMA) dynamics, a novel mathematical framework to understand the training procedure of multilayer Transformer architectures. This is achieved by integrating out the self-attention layer in Transformers, producing a modified dynamics of MLP layers only. JoMA removes unrealistic assumptions in previous analysis (e.g., lack of residual connection) and predicts that the attention first becomes sparse (to learn salient tokens), then dense (to learn less salient tokens) in the presence of nonlinear activations, while in the linear case, it is consistent with existing works that show attention becomes sparse over time. We leverage JoMA to qualitatively explains how tokens are combined to form hierarchies in multilayer Transformers, when the input tokens are generated by a latent hierarchical generative model. Experiments on models trained from real-world dataset (Wikitext2/Wikitext103) and various pre-trained models (OPT, Pythia) verify our theoretical findings.

Scan and Snap: Understanding Training Dynamics and Token Composition in 1-layer Transformer

Transformer architecture has shown impressive performance in multiple research domains and has become the backbone of many neural network models. However, there is limited understanding on how it works. In particular, with a simple predictive loss, how the representation emerges from the gradient \emph{training dynamics} remains a mystery. In this paper, for 1-layer transformer with one self-attention layer plus one decoder layer, we analyze its SGD training dynamics for the task of next token prediction in a mathematically rigorous manner. We open the black box of the dynamic process of how the self-attention layer combines input tokens, and reveal the nature of underlying inductive bias. More specifically, with the assumption (a) no positional encoding, (b) long input sequence, and (c) the decoder layer learns faster than the self-attention layer, we prove that self-attention acts as a \emph{discriminative scanning algorithm}: starting from uniform attention, it gradually attends more to distinct key tokens for a specific next token to be predicted, and pays less attention to common key tokens that occur across different next tokens. Among distinct tokens, it progressively drops attention weights, following the order of low to high co-occurrence between the key and the query token in the training set. Interestingly, this procedure does not lead to winner-takes-all, but decelerates due to a \emph{phase transition} that is controllable by the learning rates of the two layers, leaving (almost) fixed token combination. We verify this \textbf{\emph{scan and snap}} dynamics on synthetic and real-world data (WikiText).

Near-Optimal Algorithms for Autonomous Exploration and Multi-Goal Stochastic Shortest Path

We revisit the incremental autonomous exploration problem proposed by Lim & Auer (2012). In this setting, the agent aims to learn a set of near-optimal goal-conditioned policies to reach the $L$-controllable states: states that are incrementally reachable from an initial state $s_0$ within $L$ steps in expectation. We introduce a new algorithm with stronger sample complexity bounds than existing ones. Furthermore, we also prove the first lower bound for the autonomous exploration problem. In particular, the lower bound implies that our proposed algorithm, Value-Aware Autonomous Exploration, is nearly minimax-optimal when the number of $L$-controllable states grows polynomially with respect to $L$. Key in our algorithm design is a connection between autonomous exploration and multi-goal stochastic shortest path, a new problem that naturally generalizes the classical stochastic shortest path problem. This new problem and its connection to autonomous exploration can be of independent interest.

AdaLoss: A computationally-efficient and provably convergent adaptive gradient method

We propose a computationally-friendly adaptive learning rate schedule, "AdaLoss", which directly uses the information of the loss function to adjust the stepsize in gradient descent methods. We prove that this schedule enjoys linear convergence in linear regression. Moreover, we provide a linear convergence guarantee over the non-convex regime, in the context of two-layer over-parameterized neural networks. If the width of the first-hidden layer in the two-layer networks is sufficiently large (polynomially), then AdaLoss converges robustly \emph{to the global minimum} in polynomial time. We numerically verify the theoretical results and extend the scope of the numerical experiments by considering applications in LSTM models for text clarification and policy gradients for control problems.

Discovering Diverse Multi-Agent Strategic Behavior via Reward Randomization

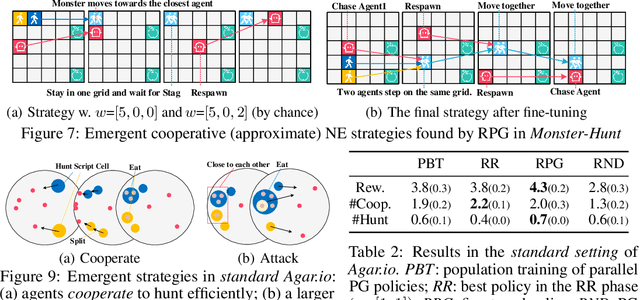
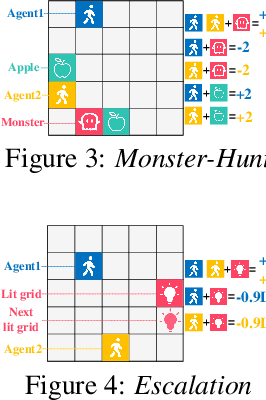
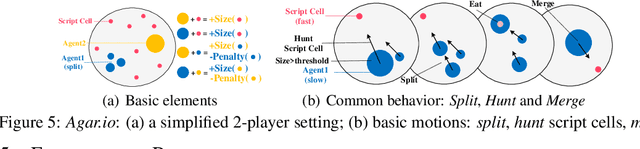
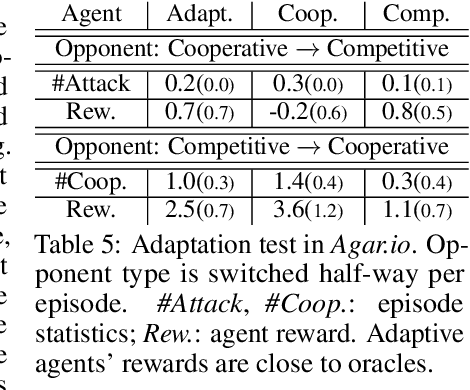
We propose a simple, general and effective technique, Reward Randomization for discovering diverse strategic policies in complex multi-agent games. Combining reward randomization and policy gradient, we derive a new algorithm, Reward-Randomized Policy Gradient (RPG). RPG is able to discover multiple distinctive human-interpretable strategies in challenging temporal trust dilemmas, including grid-world games and a real-world game Agar.io, where multiple equilibria exist but standard multi-agent policy gradient algorithms always converge to a fixed one with a sub-optimal payoff for every player even using state-of-the-art exploration techniques. Furthermore, with the set of diverse strategies from RPG, we can (1) achieve higher payoffs by fine-tuning the best policy from the set; and (2) obtain an adaptive agent by using this set of strategies as its training opponents. The source code and example videos can be found in our website: https://sites.google.com/view/staghuntrpg.

Discrete-Continuous Mixtures in Probabilistic Programming: Generalized Semantics and Inference Algorithms

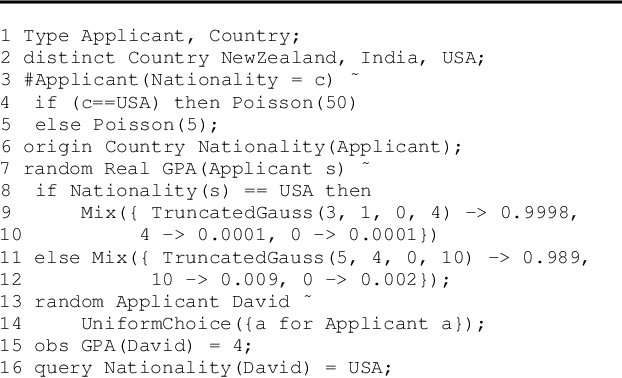
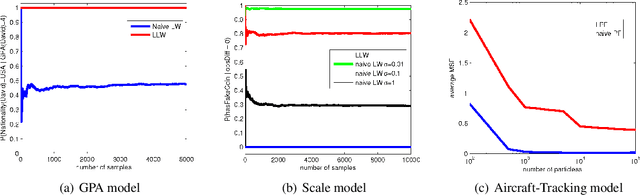
Despite the recent successes of probabilistic programming languages (PPLs) in AI applications, PPLs offer only limited support for random variables whose distributions combine discrete and continuous elements. We develop the notion of measure-theoretic Bayesian networks (MTBNs) and use it to provide more general semantics for PPLs with arbitrarily many random variables defined over arbitrary measure spaces. We develop two new general sampling algorithms that are provably correct under the MTBN framework: the lexicographic likelihood weighting (LLW) for general MTBNs and the lexicographic particle filter (LPF), a specialized algorithm for state-space models. We further integrate MTBNs into a widely used PPL system, BLOG, and verify the effectiveness of the new inference algorithms through representative examples.

Stochastic Zeroth-order Optimization in High Dimensions

We consider the problem of optimizing a high-dimensional convex function using stochastic zeroth-order queries. Under sparsity assumptions on the gradients or function values, we present two algorithms: a successive component/feature selection algorithm and a noisy mirror descent algorithm using Lasso gradient estimates, and show that both algorithms have convergence rates that de- pend only logarithmically on the ambient dimension of the problem. Empirical results confirm our theoretical findings and show that the algorithms we design outperform classical zeroth-order optimization methods in the high-dimensional setting.