Discrete-Continuous Mixtures in Probabilistic Programming: Generalized Semantics and Inference Algorithms

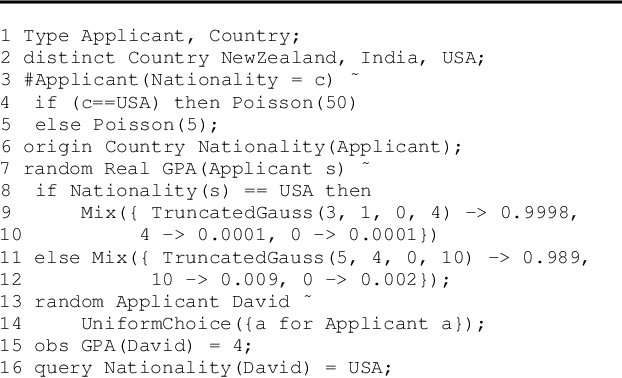
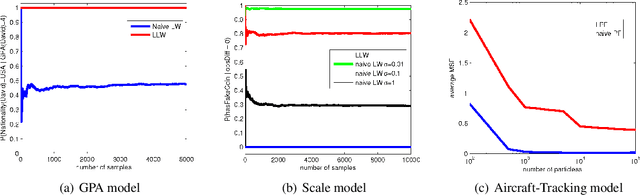
Despite the recent successes of probabilistic programming languages (PPLs) in AI applications, PPLs offer only limited support for random variables whose distributions combine discrete and continuous elements. We develop the notion of measure-theoretic Bayesian networks (MTBNs) and use it to provide more general semantics for PPLs with arbitrarily many random variables defined over arbitrary measure spaces. We develop two new general sampling algorithms that are provably correct under the MTBN framework: the lexicographic likelihood weighting (LLW) for general MTBNs and the lexicographic particle filter (LPF), a specialized algorithm for state-space models. We further integrate MTBNs into a widely used PPL system, BLOG, and verify the effectiveness of the new inference algorithms through representative examples.

Selecting Computations: Theory and Applications

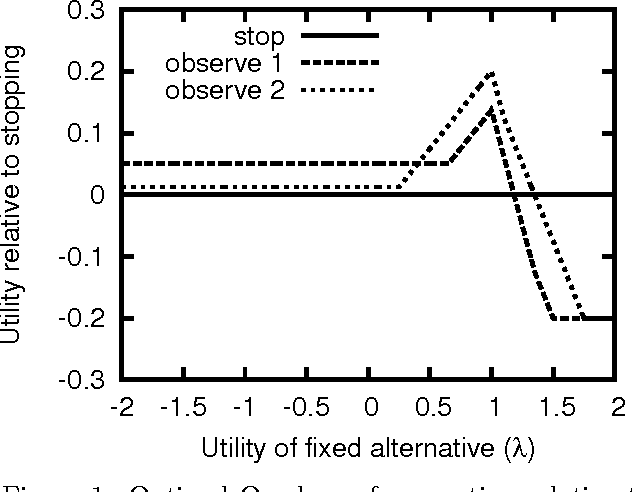
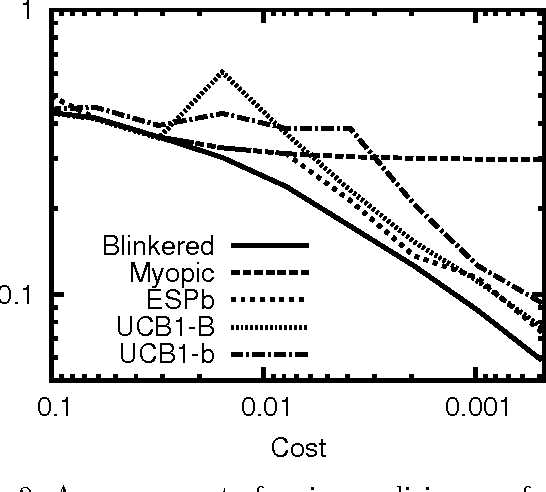
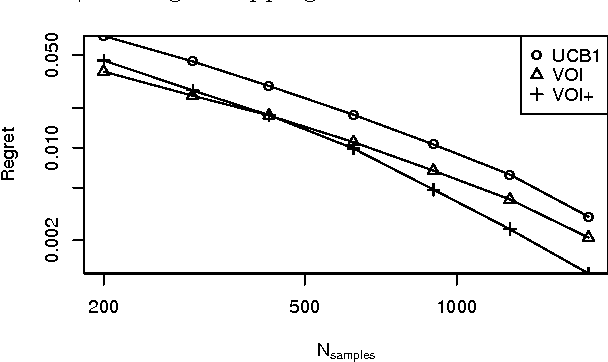
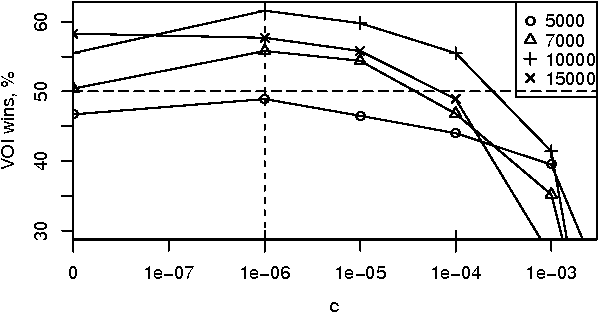
Sequential decision problems are often approximately solvable by simulating possible future action sequences. Metalevel decision procedures have been developed for selecting which action sequences to simulate, based on estimating the expected improvement in decision quality that would result from any particular simulation; an example is the recent work on using bandit algorithms to control Monte Carlo tree search in the game of Go. In this paper we develop a theoretical basis for metalevel decisions in the statistical framework of Bayesian selection problems, arguing (as others have done) that this is more appropriate than the bandit framework. We derive a number of basic results applicable to Monte Carlo selection problems, including the first finite sampling bounds for optimal policies in certain cases; we also provide a simple counterexample to the intuitive conjecture that an optimal policy will necessarily reach a decision in all cases. We then derive heuristic approximations in both Bayesian and distribution-free settings and demonstrate their superiority to bandit-based heuristics in one-shot decision problems and in Go.