Solomon Eyal Shimony
Planning and Acting While the Clock Ticks
Mar 21, 2024

Abstract:Standard temporal planning assumes that planning takes place offline and then execution starts at time 0. Recently, situated temporal planning was introduced, where planning starts at time 0 and execution occurs after planning terminates. Situated temporal planning reflects a more realistic scenario where time passes during planning. However, in situated temporal planning a complete plan must be generated before any action is executed. In some problems with time pressure, timing is too tight to complete planning before the first action must be executed. For example, an autonomous car that has a truck backing towards it should probably move out of the way now and plan how to get to its destination later. In this paper, we propose a new problem setting: concurrent planning and execution, in which actions can be dispatched (executed) before planning terminates. Unlike previous work on planning and execution, we must handle wall clock deadlines that affect action applicability and goal achievement (as in situated planning) while also supporting dispatching actions before a complete plan has been found. We extend previous work on metareasoning for situated temporal planning to develop an algorithm for this new setting. Our empirical evaluation shows that when there is strong time pressure, our approach outperforms situated temporal planning.
Estimating the Probability of Meeting a Deadline in Hierarchical Plans
Dec 24, 2017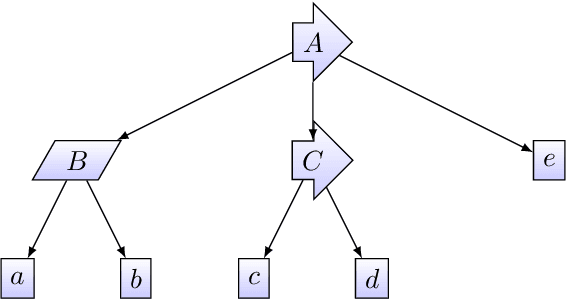
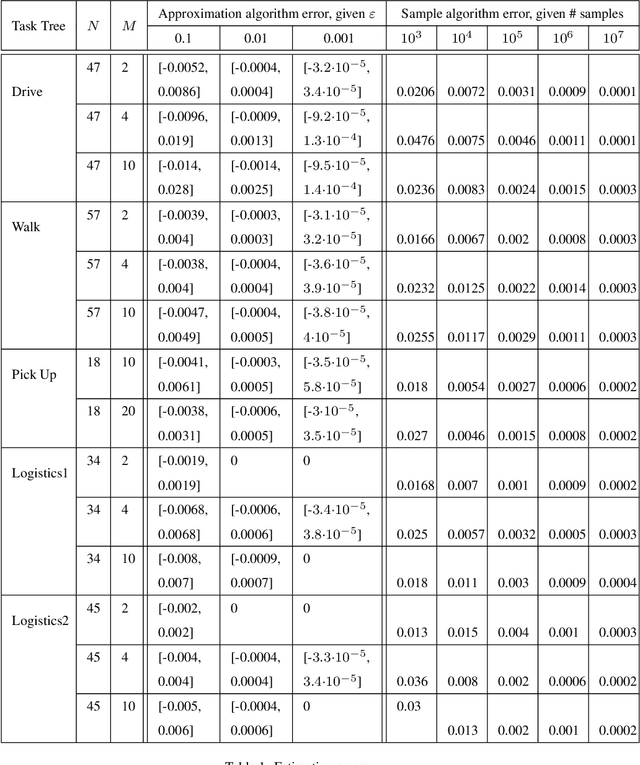
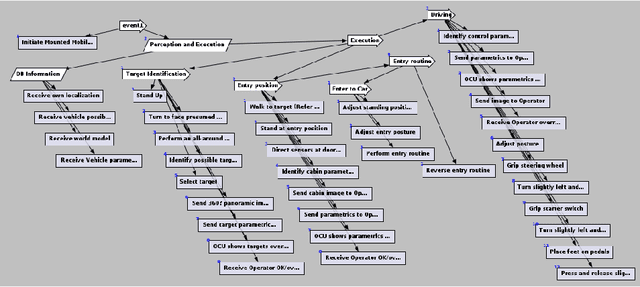
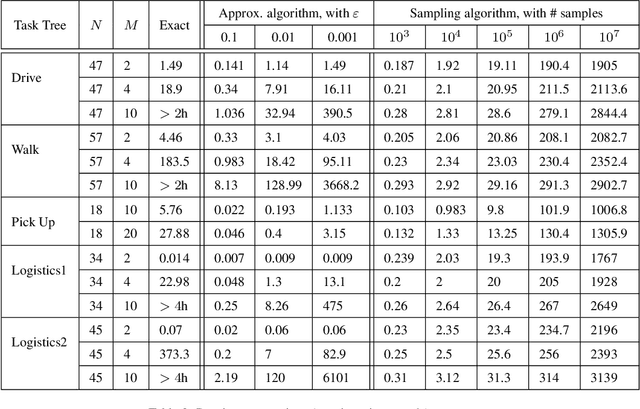
Abstract:Given a hierarchical plan (or schedule) with uncertain task times, we propose a deterministic polynomial (time and memory) algorithm for estimating the probability that its meets a deadline, or, alternately, that its {\em makespan} is less than a given duration. Approximation is needed as it is known that this problem is NP-hard even for sequential plans (just, a sum of random variables). In addition, we show two new complexity results: (1) Counting the number of events that do not cross deadline is \#P-hard; (2)~Computing the expected makespan of a hierarchical plan is NP-hard. For the proposed approximation algorithm, we establish formal approximation bounds and show that the time and memory complexities grow polynomially with the required accuracy, the number of nodes in the plan, and with the size of the support of the random variables that represent the durations of the primitive tasks. We examine these approximation bounds empirically and demonstrate, using task networks taken from the literature, how our scheme outperforms sampling techniques and exact computation in terms of accuracy and run-time. As the empirical data shows much better error bounds than guaranteed, we also suggest a method for tightening the bounds in some cases.
Rational Deployment of Multiple Heuristics in IDA*
Nov 24, 2014



Abstract:Recent advances in metareasoning for search has shown its usefulness in improving numerous search algorithms. This paper applies rational metareasoning to IDA* when several admissible heuristics are available. The obvious basic approach of taking the maximum of the heuristics is improved upon by lazy evaluation of the heuristics, resulting in a variant known as Lazy IDA*. We introduce a rational version of lazy IDA* that decides whether to compute the more expensive heuristics or to bypass it, based on a myopic expected regret estimate. Empirical evaluation in several domains supports the theoretical results, and shows that rational lazy IDA* is a state-of-the-art heuristic combination method.
Selecting Computations: Theory and Applications
Aug 09, 2014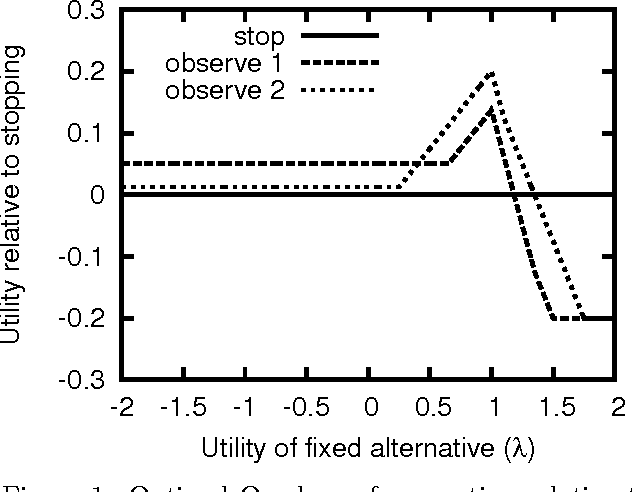
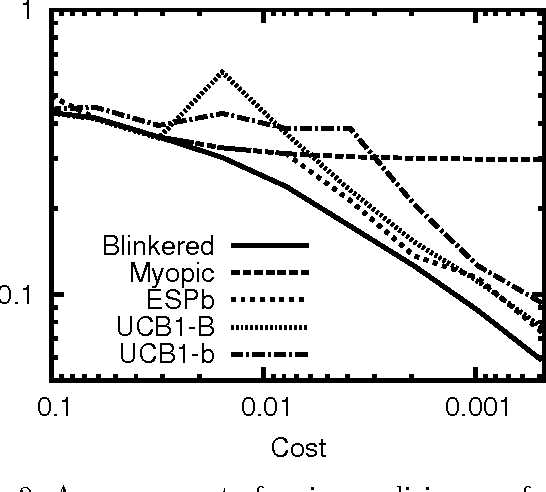
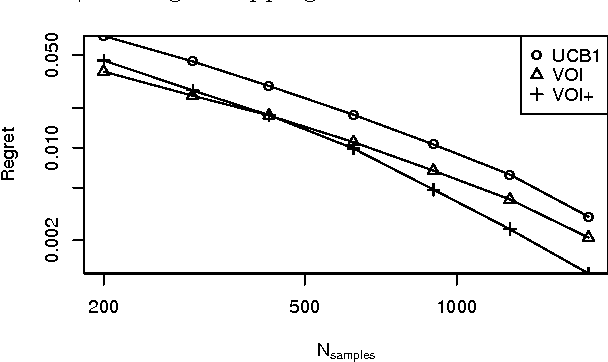
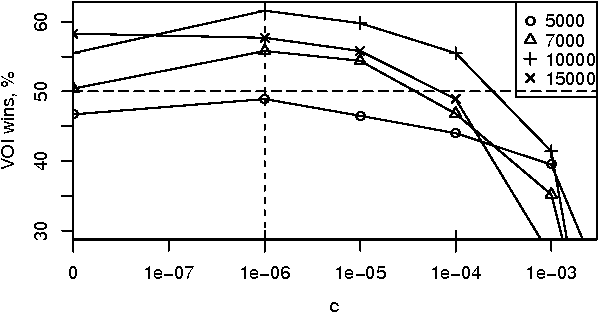
Abstract:Sequential decision problems are often approximately solvable by simulating possible future action sequences. Metalevel decision procedures have been developed for selecting which action sequences to simulate, based on estimating the expected improvement in decision quality that would result from any particular simulation; an example is the recent work on using bandit algorithms to control Monte Carlo tree search in the game of Go. In this paper we develop a theoretical basis for metalevel decisions in the statistical framework of Bayesian selection problems, arguing (as others have done) that this is more appropriate than the bandit framework. We derive a number of basic results applicable to Monte Carlo selection problems, including the first finite sampling bounds for optimal policies in certain cases; we also provide a simple counterexample to the intuitive conjecture that an optimal policy will necessarily reach a decision in all cases. We then derive heuristic approximations in both Bayesian and distribution-free settings and demonstrate their superiority to bandit-based heuristics in one-shot decision problems and in Go.
Generic Preferences over Subsets of Structured Objects
Jan 15, 2014
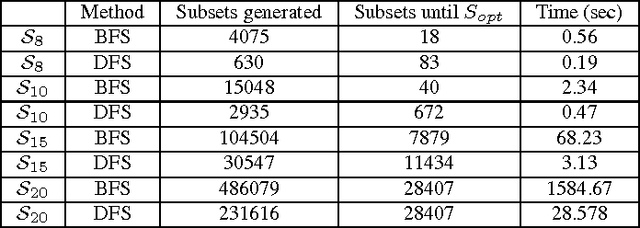
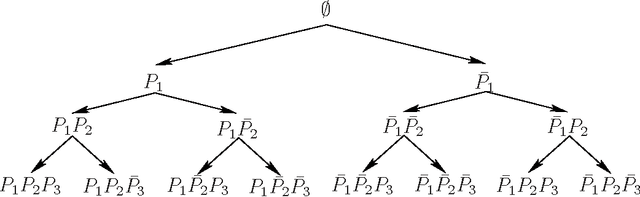
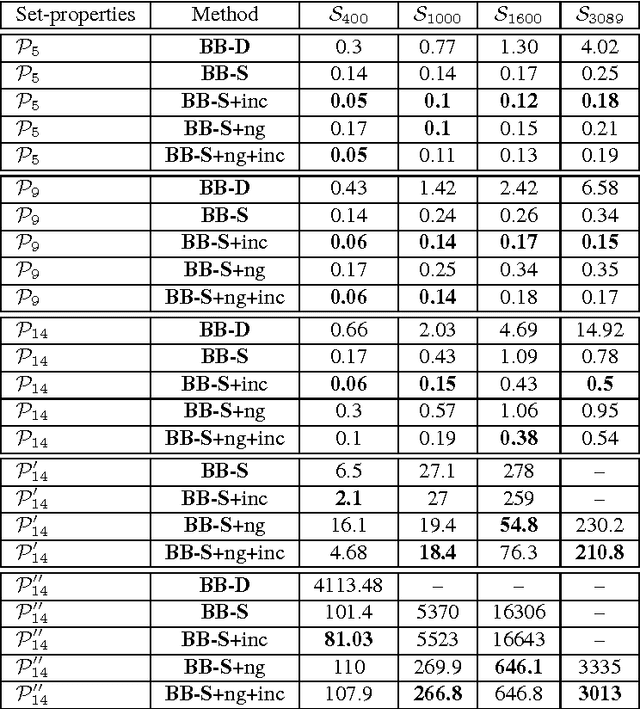
Abstract:Various tasks in decision making and decision support systems require selecting a preferred subset of a given set of items. Here we focus on problems where the individual items are described using a set of characterizing attributes, and a generic preference specification is required, that is, a specification that can work with an arbitrary set of items. For example, preferences over the content of an online newspaper should have this form: At each viewing, the newspaper contains a subset of the set of articles currently available. Our preference specification over this subset should be provided offline, but we should be able to use it to select a subset of any currently available set of articles, e.g., based on their tags. We present a general approach for lifting formalisms for specifying preferences over objects with multiple attributes into ones that specify preferences over subsets of such objects. We also show how we can compute an optimal subset given such a specification in a relatively efficient manner. We provide an empirical evaluation of the approach as well as some worst-case complexity results.
Towards Rational Deployment of Multiple Heuristics in A*
May 22, 2013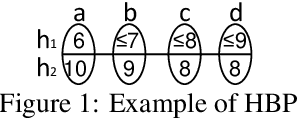
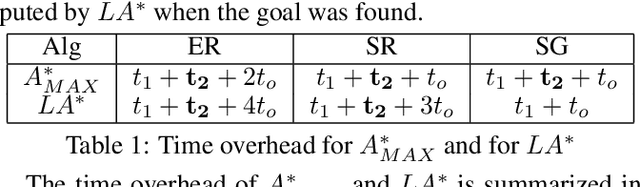
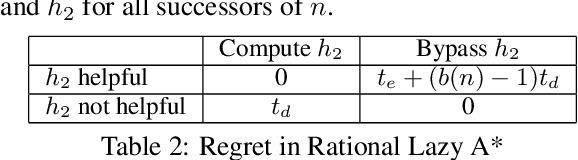

Abstract:The obvious way to use several admissible heuristics in A* is to take their maximum. In this paper we aim to reduce the time spent on computing heuristics. We discuss Lazy A*, a variant of A* where heuristics are evaluated lazily: only when they are essential to a decision to be made in the A* search process. We present a new rational meta-reasoning based scheme, rational lazy A*, which decides whether to compute the more expensive heuristics at all, based on a myopic value of information estimate. Both methods are examined theoretically. Empirical evaluation on several domains supports the theoretical results, and shows that lazy A* and rational lazy A* are state-of-the-art heuristic combination methods.
A New Algorithm for Finding MAP Assignments to Belief Networks
Mar 27, 2013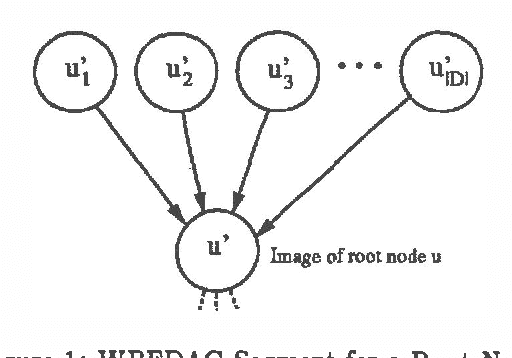
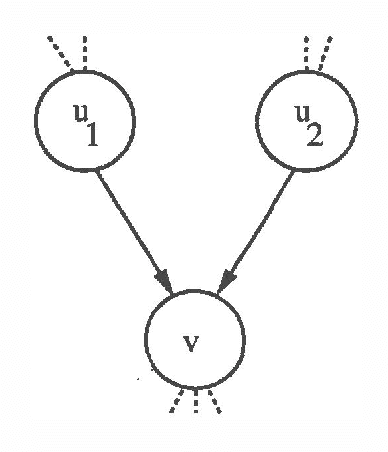
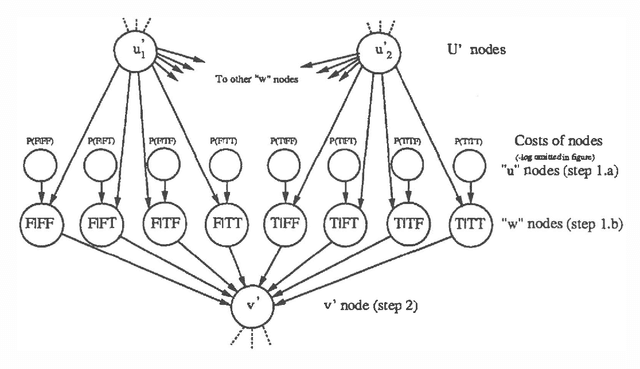
Abstract:We present a new algorithm for finding maximum a-posterior) (MAP) assignments of values to belief networks. The belief network is compiled into a network consisting only of nodes with boolean (i.e. only 0 or 1) conditional probabilities. The MAP assignment is then found using a best-first search on the resulting network. We argue that, as one would anticipate, the algorithm is exponential for the general case, but only linear in the size of the network for poly trees.
Algorithms for Irrelevance-Based Partial MAPs
Mar 20, 2013


Abstract:Irrelevance-based partial MAPs are useful constructs for domain-independent explanation using belief networks. We look at two definitions for such partial MAPs, and prove important properties that are useful in designing algorithms for computing them effectively. We make use of these properties in modifying our standard MAP best-first algorithm, so as to handle irrelevance-based partial MAPs.
Relevant Explanations: Allowing Disjunctive Assignments
Mar 06, 2013

Abstract:Relevance-based explanation is a scheme in which partial assignments to Bayesian belief network variables are explanations (abductive conclusions). We allow variables to remain unassigned in explanations as long as they are irrelevant to the explanation, where irrelevance is defined in terms of statistical independence. When multiple-valued variables exist in the system, especially when subsets of values correspond to natural types of events, the over specification problem, alleviated by independence-based explanation, resurfaces. As a solution to that, as well as for addressing the question of explanation specificity, it is desirable to collapse such a subset of values into a single value on the fly. The equivalent method, which is adopted here, is to generalize the notion of assignments to allow disjunctive assignments. We proceed to define generalized independence based explanations as maximum posterior probability independence based generalized assignments (GIB-MAPs). GIB assignments are shown to have certain properties that ease the design of algorithms for computing GIB-MAPs. One such algorithm is discussed here, as well as suggestions for how other algorithms may be adapted to compute GIB-MAPs. GIB-MAP explanations still suffer from instability, a problem which may be addressed using ?approximate? conditional independence as a condition for irrelevance.
Belief Updating by Enumerating High-Probability Independence-Based Assignments
Feb 27, 2013
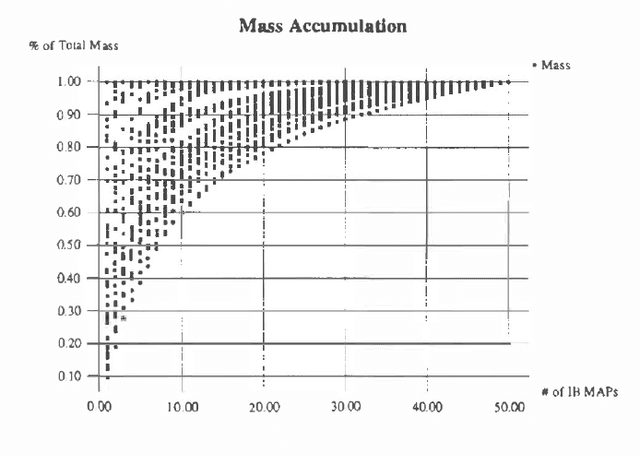
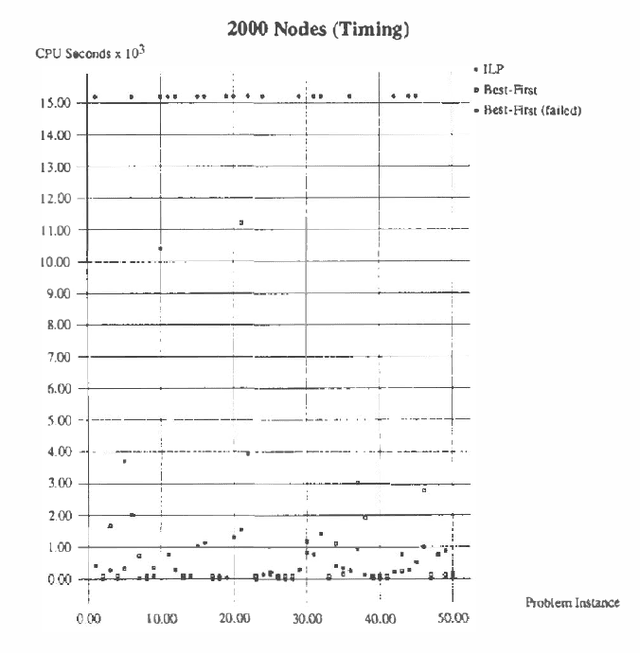
Abstract:Independence-based (IB) assignments to Bayesian belief networks were originally proposed as abductive explanations. IB assignments assign fewer variables in abductive explanations than do schemes assigning values to all evidentially supported variables. We use IB assignments to approximate marginal probabilities in Bayesian belief networks. Recent work in belief updating for Bayes networks attempts to approximate posterior probabilities by finding a small number of the highest probability complete (or perhaps evidentially supported) assignments. Under certain assumptions, the probability mass in the union of these assignments is sufficient to obtain a good approximation. Such methods are especially useful for highly-connected networks, where the maximum clique size or the cutset size make the standard algorithms intractable. Since IB assignments contain fewer assigned variables, the probability mass in each assignment is greater than in the respective complete assignment. Thus, fewer IB assignments are sufficient, and a good approximation can be obtained more efficiently. IB assignments can be used for efficiently approximating posterior node probabilities even in cases which do not obey the rather strict skewness assumptions used in previous research. Two algorithms for finding the high probability IB assignments are suggested: one by doing a best-first heuristic search, and another by special-purpose integer linear programming. Experimental results show that this approach is feasible for highly connected belief networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge