A Behavior-Based Knowledge Representation Improves Prediction of Players' Moves in Chess by 25%

Predicting player behavior in strategic games, especially complex ones like chess, presents a significant challenge. The difficulty arises from several factors. First, the sheer number of potential outcomes stemming from even a single position, starting from the initial setup, makes forecasting a player's next move incredibly complex. Second, and perhaps even more challenging, is the inherent unpredictability of human behavior. Unlike the optimized play of engines, humans introduce a layer of variability due to differing playing styles and decision-making processes. Each player approaches the game with a unique blend of strategic thinking, tactical awareness, and psychological tendencies, leading to diverse and often unexpected actions. This stylistic variation, combined with the capacity for creativity and even irrational moves, makes predicting human play difficult. Chess, a longstanding benchmark of artificial intelligence research, has seen significant advancements in tools and automation. Engines like Deep Blue, AlphaZero, and Stockfish can defeat even the most skilled human players. However, despite their exceptional ability to outplay top-level grandmasters, predicting the moves of non-grandmaster players, who comprise most of the global chess community -- remains complicated for these engines. This paper proposes a novel approach combining expert knowledge with machine learning techniques to predict human players' next moves. By applying feature engineering grounded in domain expertise, we seek to uncover the patterns in the moves of intermediate-level chess players, particularly during the opening phase of the game. Our methodology offers a promising framework for anticipating human behavior, advancing both the fields of AI and human-computer interaction.

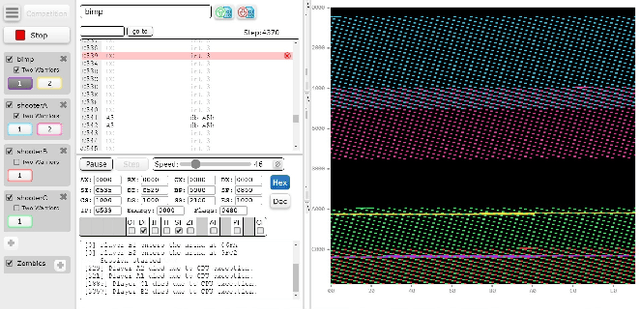
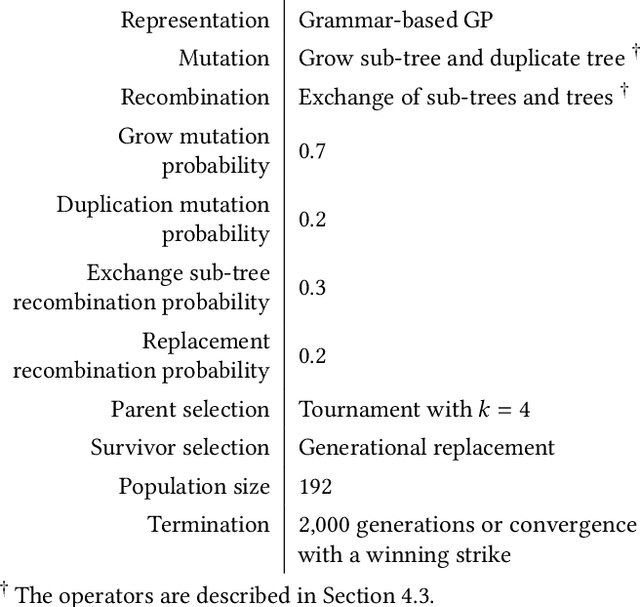
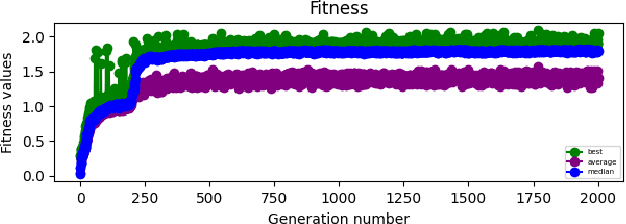
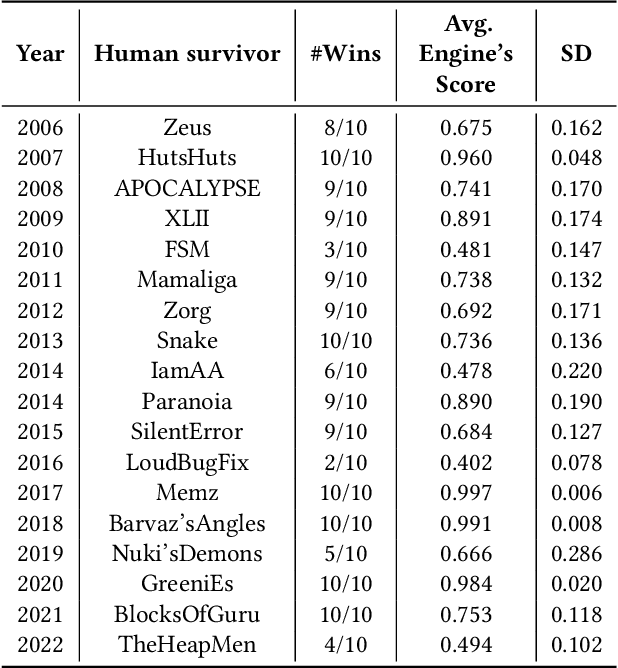
Evolving Assembly Code in an Adversarial Environment

In this work, we evolve assembly code for the CodeGuru competition. The competition's goal is to create a survivor -- an assembly program that runs the longest in shared memory, by resisting attacks from adversary survivors and finding their weaknesses. For evolving top-notch solvers, we specify a Backus Normal Form (BNF) for the assembly language and synthesize the code from scratch using Genetic Programming (GP). We evaluate the survivors by running CodeGuru games against human-written winning survivors. Our evolved programs found weaknesses in the programs they were trained against and utilized them. In addition, we compare our approach with a Large-Language Model, demonstrating that the latter cannot generate a survivor that can win at any competition. This work has important applications for cyber-security, as we utilize evolution to detect weaknesses in survivors. The assembly BNF is domain-independent; thus, by modifying the fitness function, it can detect code weaknesses and help fix them. Finally, the CodeGuru competition offers a novel platform for analyzing GP and code evolution in adversarial environments. To support further research in this direction, we provide a thorough qualitative analysis of the evolved survivors and the weaknesses found.

Efficient One Sided Kolmogorov Approximation

We present an efficient algorithm that, given a discrete random variable $X$ and a number $m$, computes a random variable whose support is of size at most $m$ and whose Kolmogorov distance from $X$ is minimal, also for the one-sided Kolmogorov approximation. We present some variants of the algorithm, analyse their correctness and computational complexity, and present a detailed empirical evaluation that shows how they performs in practice. The main application that we examine, which is our motivation for this work, is estimation of the probability missing deadlines in series-parallel schedules. Since exact computation of these probabilities is NP-hard, we propose to use the algorithms described in this paper to obtain an approximation.

An optimal approximation of discrete random variables with respect to the Kolmogorov distance

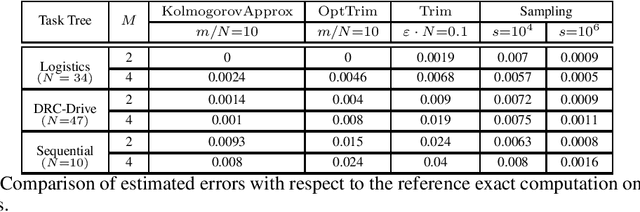
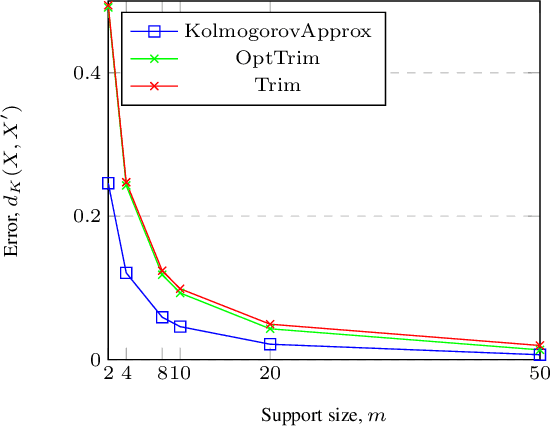
We present an algorithm that takes a discrete random variable $X$ and a number $m$ and computes a random variable whose support (set of possible outcomes) is of size at most $m$ and whose Kolmogorov distance from $X$ is minimal. In addition to a formal theoretical analysis of the correctness and of the computational complexity of the algorithm, we present a detailed empirical evaluation that shows how the proposed approach performs in practice in different applications and domains.

Estimating the Probability of Meeting a Deadline in Hierarchical Plans

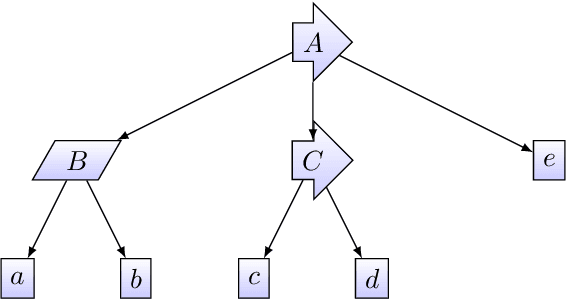
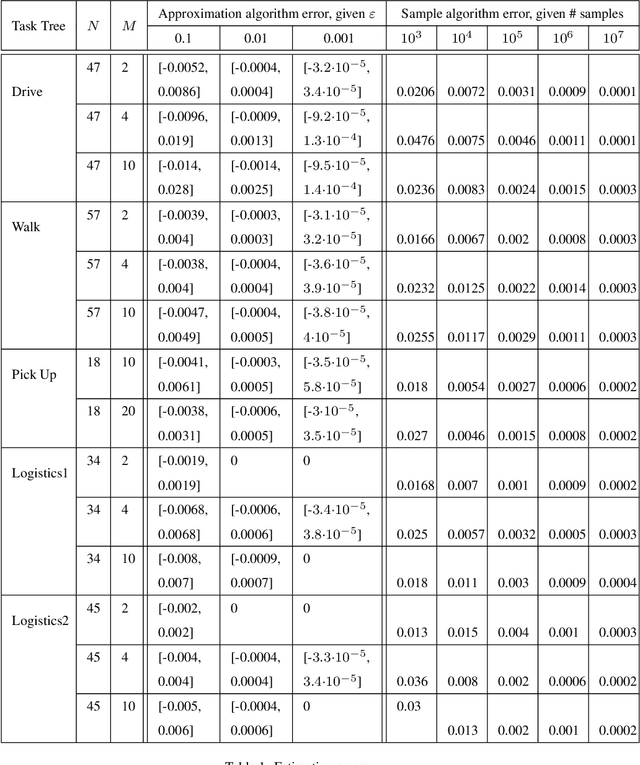
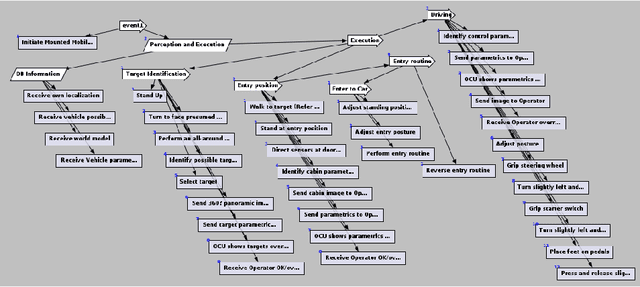
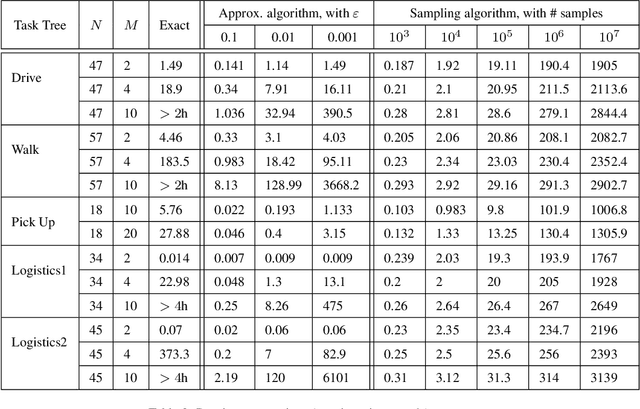
Given a hierarchical plan (or schedule) with uncertain task times, we propose a deterministic polynomial (time and memory) algorithm for estimating the probability that its meets a deadline, or, alternately, that its {\em makespan} is less than a given duration. Approximation is needed as it is known that this problem is NP-hard even for sequential plans (just, a sum of random variables). In addition, we show two new complexity results: (1) Counting the number of events that do not cross deadline is \#P-hard; (2)~Computing the expected makespan of a hierarchical plan is NP-hard. For the proposed approximation algorithm, we establish formal approximation bounds and show that the time and memory complexities grow polynomially with the required accuracy, the number of nodes in the plan, and with the size of the support of the random variables that represent the durations of the primitive tasks. We examine these approximation bounds empirically and demonstrate, using task networks taken from the literature, how our scheme outperforms sampling techniques and exact computation in terms of accuracy and run-time. As the empirical data shows much better error bounds than guaranteed, we also suggest a method for tightening the bounds in some cases.