Deep Learning Models for Automated Classification of Dog Emotional States from Facial Expressions

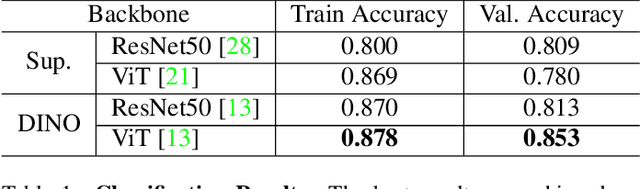
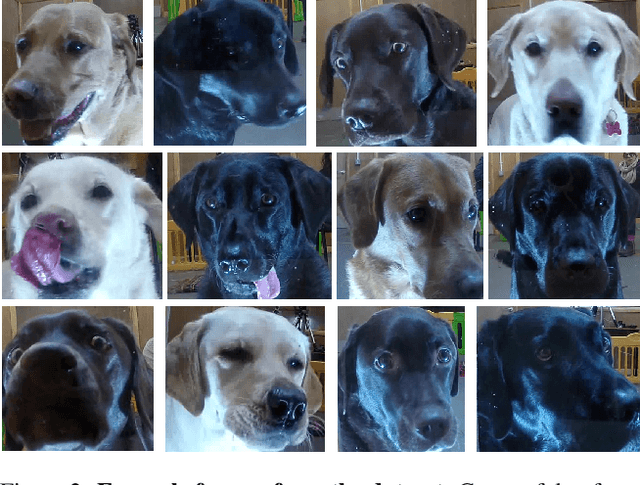
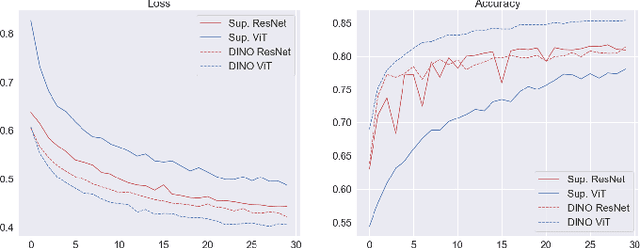
Similarly to humans, facial expressions in animals are closely linked with emotional states. However, in contrast to the human domain, automated recognition of emotional states from facial expressions in animals is underexplored, mainly due to difficulties in data collection and establishment of ground truth concerning emotional states of non-verbal users. We apply recent deep learning techniques to classify (positive) anticipation and (negative) frustration of dogs on a dataset collected in a controlled experimental setting. We explore the suitability of different backbones (e.g. ResNet, ViT) under different supervisions to this task, and find that features of a self-supervised pretrained ViT (DINO-ViT) are superior to the other alternatives. To the best of our knowledge, this work is the first to address the task of automatic classification of canine emotions on data acquired in a controlled experiment.

Mimicking Behaviors in Separated Domains

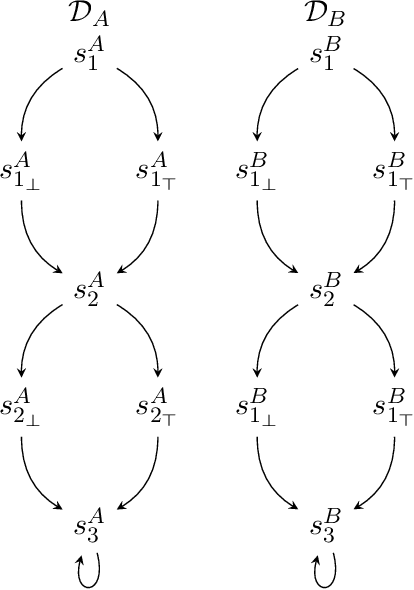
Devising a strategy to make a system mimicking behaviors from another system is a problem that naturally arises in many areas of Computer Science. In this work, we interpret this problem in the context of intelligent agents, from the perspective of LTLf, a formalism commonly used in AI for expressing finite-trace properties. Our model consists of two separated dynamic domains, D_A and D_B, and an LTLf specification that formalizes the notion of mimicking by mapping properties on behaviors (traces) of D_A into properties on behaviors of D_B. The goal is to synthesize a strategy that step-by-step maps every behavior of D_A into a behavior of D_B so that the specification is met. We consider several forms of mapping specifications, ranging from simple ones to full LTLf, and for each we study synthesis algorithms and computational properties.

Taming Discrete Integration via the Boon of Dimensionality

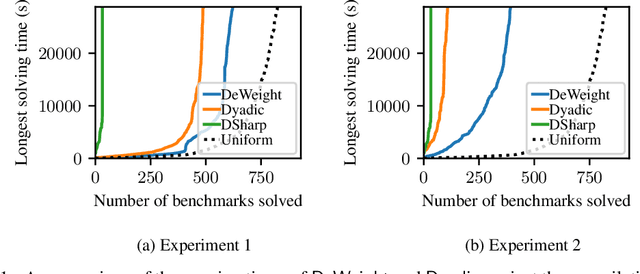
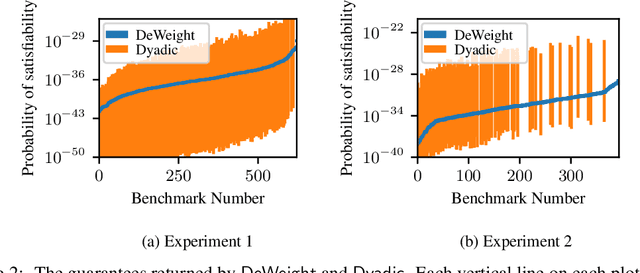
Discrete integration is a fundamental problem in computer science that concerns the computation of discrete sums over exponentially large sets. Despite intense interest from researchers for over three decades, the design of scalable techniques for computing estimates with rigorous guarantees for discrete integration remains the holy grail. The key contribution of this work addresses this scalability challenge via an efficient reduction of discrete integration to model counting. The proposed reduction is achieved via a significant increase in the dimensionality that, contrary to conventional wisdom, leads to solving an instance of the relatively simpler problem of model counting. Building on the promising approach proposed by Chakraborty et al, our work overcomes the key weakness of their approach: a restriction to dyadic weights. We augment our proposed reduction, called DeWeight, with a state of the art efficient approximate model counter and perform detailed empirical analysis over benchmarks arising from neural network verification domains, an emerging application area of critical importance. DeWeight, to the best of our knowledge, is the first technique to compute estimates with provable guarantees for this class of benchmarks.

An optimal approximation of discrete random variables with respect to the Kolmogorov distance

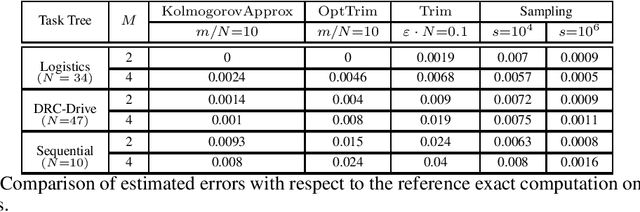
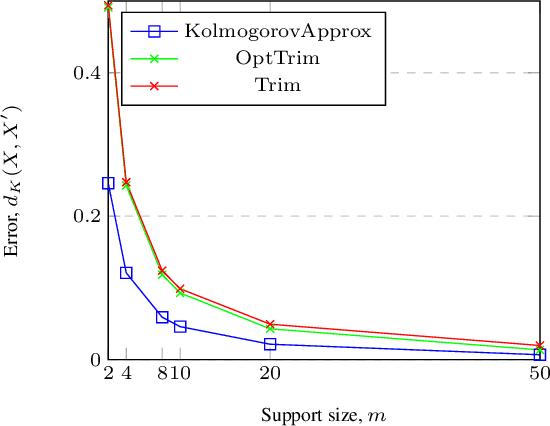
We present an algorithm that takes a discrete random variable $X$ and a number $m$ and computes a random variable whose support (set of possible outcomes) is of size at most $m$ and whose Kolmogorov distance from $X$ is minimal. In addition to a formal theoretical analysis of the correctness and of the computational complexity of the algorithm, we present a detailed empirical evaluation that shows how the proposed approach performs in practice in different applications and domains.

Constrained Sampling and Counting: Universal Hashing Meets SAT Solving

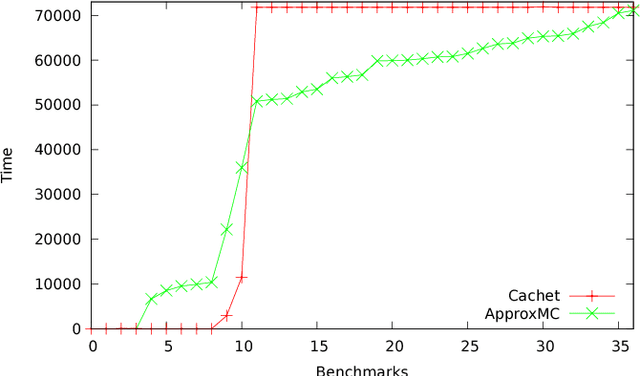
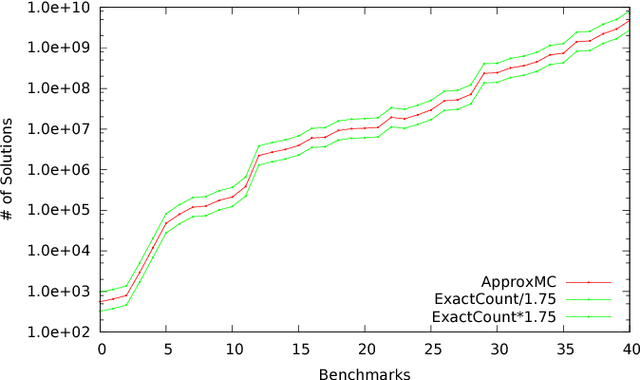
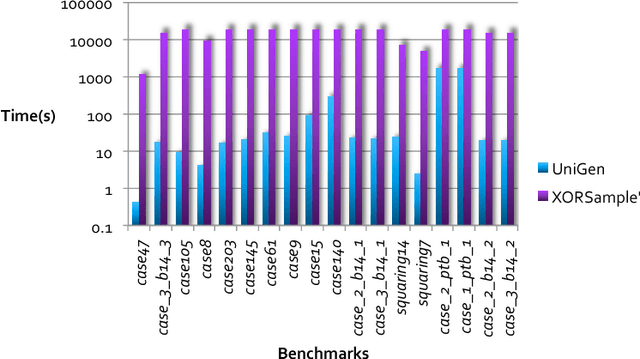
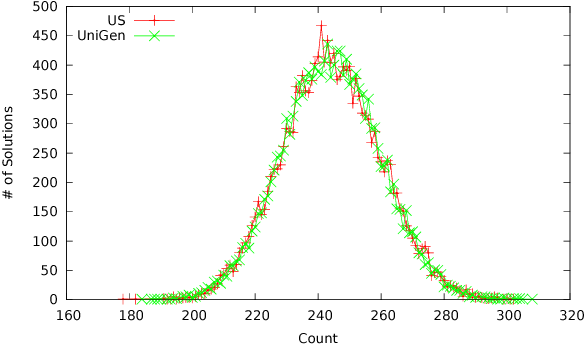
Constrained sampling and counting are two fundamental problems in artificial intelligence with a diverse range of applications, spanning probabilistic reasoning and planning to constrained-random verification. While the theory of these problems was thoroughly investigated in the 1980s, prior work either did not scale to industrial size instances or gave up correctness guarantees to achieve scalability. Recently, we proposed a novel approach that combines universal hashing and SAT solving and scales to formulas with hundreds of thousands of variables without giving up correctness guarantees. This paper provides an overview of the key ingredients of the approach and discusses challenges that need to be overcome to handle larger real-world instances.