Taming Discrete Integration via the Boon of Dimensionality

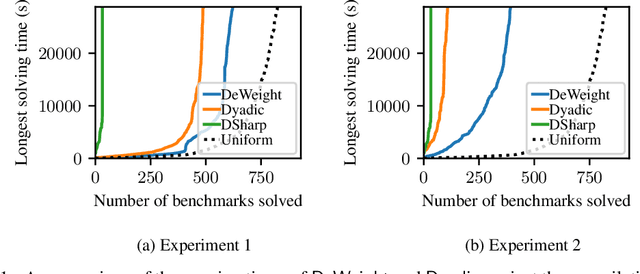
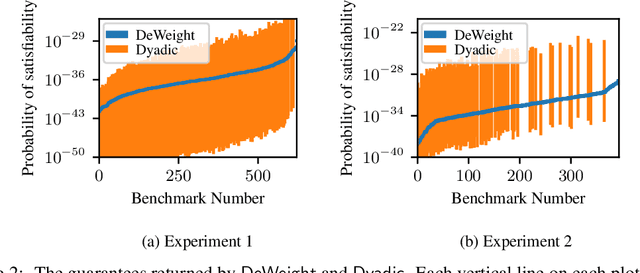
Discrete integration is a fundamental problem in computer science that concerns the computation of discrete sums over exponentially large sets. Despite intense interest from researchers for over three decades, the design of scalable techniques for computing estimates with rigorous guarantees for discrete integration remains the holy grail. The key contribution of this work addresses this scalability challenge via an efficient reduction of discrete integration to model counting. The proposed reduction is achieved via a significant increase in the dimensionality that, contrary to conventional wisdom, leads to solving an instance of the relatively simpler problem of model counting. Building on the promising approach proposed by Chakraborty et al, our work overcomes the key weakness of their approach: a restriction to dyadic weights. We augment our proposed reduction, called DeWeight, with a state of the art efficient approximate model counter and perform detailed empirical analysis over benchmarks arising from neural network verification domains, an emerging application area of critical importance. DeWeight, to the best of our knowledge, is the first technique to compute estimates with provable guarantees for this class of benchmarks.

DPMC: Weighted Model Counting by Dynamic Programming on Project-Join Trees

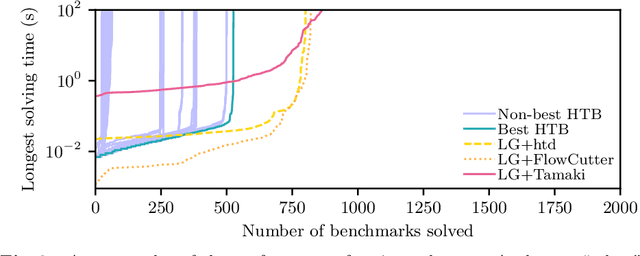
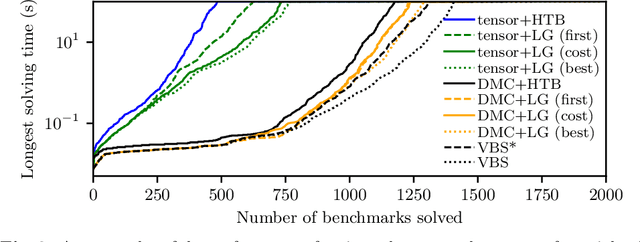
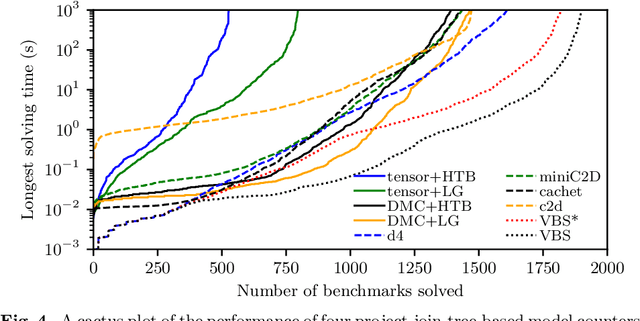
We propose a unifying dynamic-programming framework to compute exact literal-weighted model counts of formulas in conjunctive normal form. At the center of our framework are project-join trees, which specify efficient project-join orders to apply additive projections (variable eliminations) and joins (clause multiplications). In this framework, model counting is performed in two phases. First, the planning phase constructs a project-join tree from a formula. Second, the execution phase computes the model count of the formula, employing dynamic programming as guided by the project-join tree. We empirically evaluate various methods for the planning phase and compare constraint-satisfaction heuristics with tree-decomposition tools. We also investigate the performance of different data structures for the execution phase and compare algebraic decision diagrams with tensors. We show that our dynamic-programming model-counting framework DPMC is competitive with the state-of-the-art exact weighted model counters cachet, c2d, d4, and miniC2D.

Efficient Contraction of Large Tensor Networks for Weighted Model Counting through Graph Decompositions

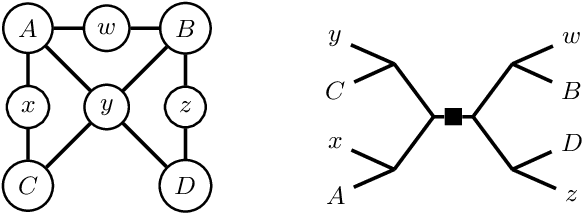
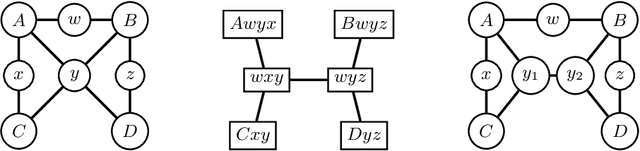
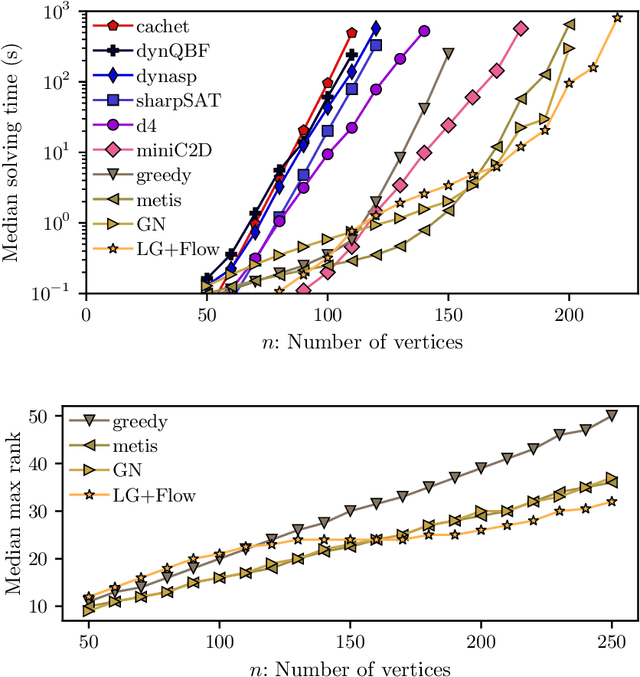
Constrained counting is a fundamental problem in artificial intelligence. A promising new algebraic approach to constrained counting makes use of tensor networks, following a reduction from constrained counting to the problem of tensor-network contraction. Contracting a tensor network efficiently requires determining an efficient order to contract the tensors inside the network, which is itself a difficult problem. In this work, we apply graph decompositions to find contraction orders for tensor networks. We prove that finding an efficient contraction order for a tensor network is equivalent to the well-known problem of finding an optimal carving decomposition. Thus memory-optimal contraction orders for planar tensor networks can be found in cubic time. We show that tree decompositions can be used both to find carving decompositions and to factor tensor networks with high-rank, structured tensors. We implement these algorithms on top of state-of-the-art solvers for tree decompositions and show empirically that the resulting weighted model counter is quite effective and useful as part of a portfolio of counters.

ADDMC: Exact Weighted Model Counting with Algebraic Decision Diagrams

We compute exact literal-weighted model counts of CNF formulas. Our algorithm employs dynamic programming, with Algebraic Decision Diagrams as the primary data structure. This technique is implemented in ADDMC, a new model counter. We empirically evaluate various heuristics that can be used with ADDMC. We also compare ADDMC to state-of-the-art exact model counters (Cachet, c2d, d4, miniC2D, and sharpSAT) on the two largest CNF model counting benchmark families (BayesNet and Planning). ADDMC solves the most benchmarks in total within the given timeout.