Efficient Contraction of Large Tensor Networks for Weighted Model Counting through Graph Decompositions

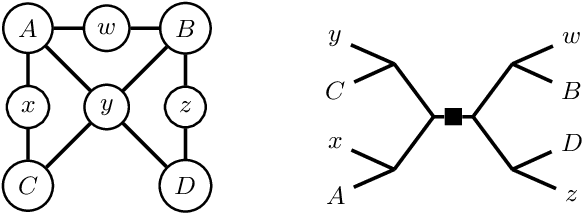
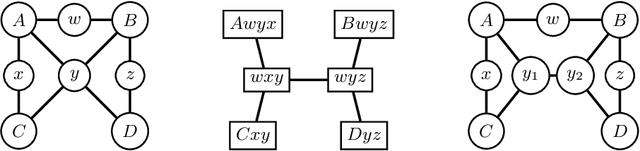
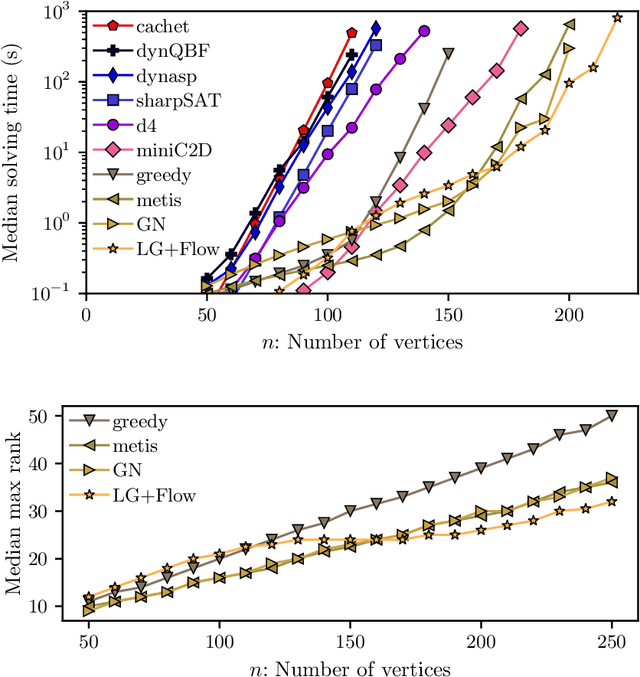
Constrained counting is a fundamental problem in artificial intelligence. A promising new algebraic approach to constrained counting makes use of tensor networks, following a reduction from constrained counting to the problem of tensor-network contraction. Contracting a tensor network efficiently requires determining an efficient order to contract the tensors inside the network, which is itself a difficult problem. In this work, we apply graph decompositions to find contraction orders for tensor networks. We prove that finding an efficient contraction order for a tensor network is equivalent to the well-known problem of finding an optimal carving decomposition. Thus memory-optimal contraction orders for planar tensor networks can be found in cubic time. We show that tree decompositions can be used both to find carving decompositions and to factor tensor networks with high-rank, structured tensors. We implement these algorithms on top of state-of-the-art solvers for tree decompositions and show empirically that the resulting weighted model counter is quite effective and useful as part of a portfolio of counters.