DPMC: Weighted Model Counting by Dynamic Programming on Project-Join Trees
Paper and Code
Aug 20, 2020
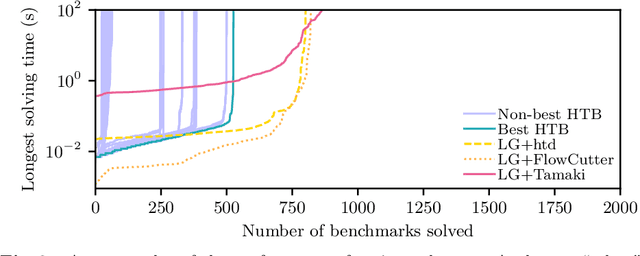
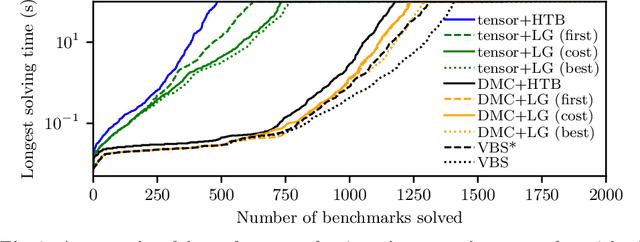
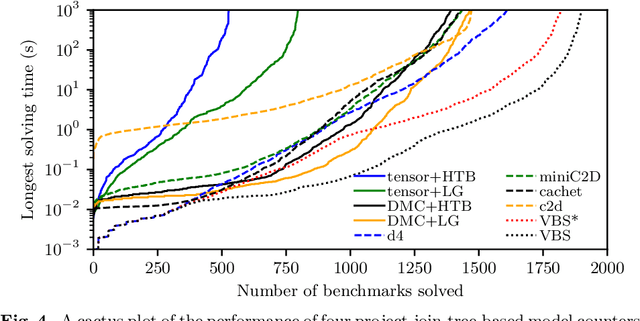
We propose a unifying dynamic-programming framework to compute exact literal-weighted model counts of formulas in conjunctive normal form. At the center of our framework are project-join trees, which specify efficient project-join orders to apply additive projections (variable eliminations) and joins (clause multiplications). In this framework, model counting is performed in two phases. First, the planning phase constructs a project-join tree from a formula. Second, the execution phase computes the model count of the formula, employing dynamic programming as guided by the project-join tree. We empirically evaluate various methods for the planning phase and compare constraint-satisfaction heuristics with tree-decomposition tools. We also investigate the performance of different data structures for the execution phase and compare algebraic decision diagrams with tensors. We show that our dynamic-programming model-counting framework DPMC is competitive with the state-of-the-art exact weighted model counters cachet, c2d, d4, and miniC2D.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge