Constrained Sampling and Counting: Universal Hashing Meets SAT Solving

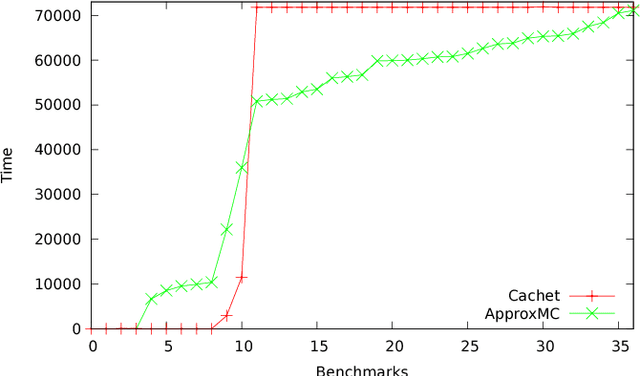
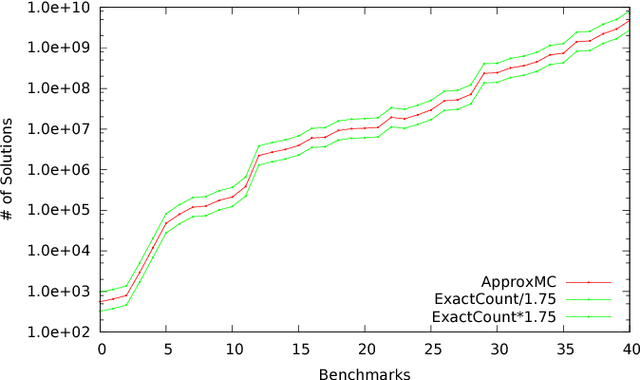
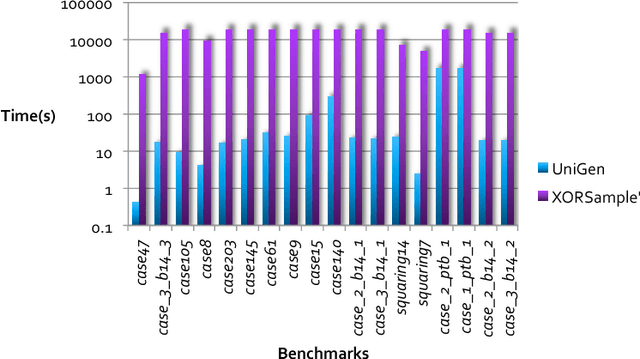
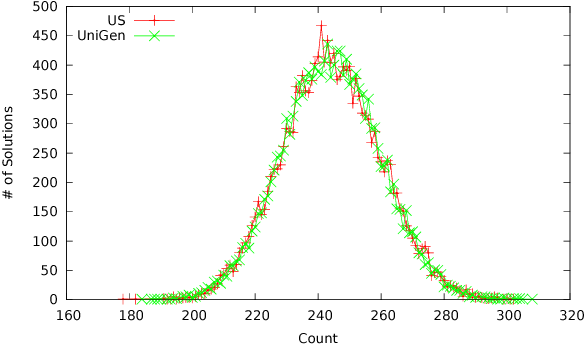
Constrained sampling and counting are two fundamental problems in artificial intelligence with a diverse range of applications, spanning probabilistic reasoning and planning to constrained-random verification. While the theory of these problems was thoroughly investigated in the 1980s, prior work either did not scale to industrial size instances or gave up correctness guarantees to achieve scalability. Recently, we proposed a novel approach that combines universal hashing and SAT solving and scales to formulas with hundreds of thousands of variables without giving up correctness guarantees. This paper provides an overview of the key ingredients of the approach and discusses challenges that need to be overcome to handle larger real-world instances.

The Computational Complexity of Structure-Based Causality

Halpern and Pearl introduced a definition of actual causality; Eiter and Lukasiewicz showed that computing whether X=x is a cause of Y=y is NP-complete in binary models (where all variables can take on only two values) and\ Sigma_2^P-complete in general models. In the final version of their paper, Halpern and Pearl slightly modified the definition of actual cause, in order to deal with problems pointed by Hopkins and Pearl. As we show, this modification has a nontrivial impact on the complexity of computing actual cause. To characterize the complexity, a new family D_k^P, k= 1, 2, 3, ..., of complexity classes is introduced, which generalizes the class DP introduced by Papadimitriou and Yannakakis (DP is just D_1^P). %joe2 %We show that the complexity of computing causality is $\D_2$-complete %under the new definition. Chockler and Halpern \citeyear{CH04} extended the We show that the complexity of computing causality under the updated definition is $D_2^P$-complete. Chockler and Halpern extended the definition of causality by introducing notions of responsibility and blame. The complexity of determining the degree of responsibility and blame using the original definition of causality was completely characterized. Again, we show that changing the definition of causality affects the complexity, and completely characterize it using the updated definition.