Multi-Object Active Search and Tracking by Multiple Agents in Untrusted, Dynamically Changing Environments

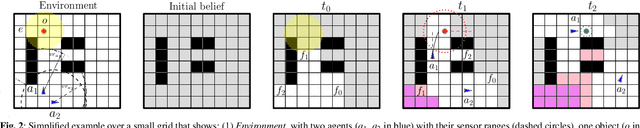
This paper addresses the problem of both actively searching and tracking multiple unknown dynamic objects in a known environment with multiple cooperative autonomous agents with partial observability. The tracking of a target ends when the uncertainty is below a threshold. Current methods typically assume homogeneous agents without access to external information and utilize short-horizon target predictive models. Such assumptions limit real-world applications. We propose a fully integrated pipeline where the main contributions are: (1) a time-varying weighted belief representation capable of handling knowledge that changes over time, which includes external reports of varying levels of trustworthiness in addition to the agents; (2) the integration of a Long Short Term Memory-based trajectory prediction within the optimization framework for long-horizon decision-making, which reasons in time-configuration space, thus increasing responsiveness; and (3) a comprehensive system that accounts for multiple agents and enables information-driven optimization. When communication is available, our strategy consolidates exploration results collected asynchronously by agents and external sources into a headquarters, who can allocate each agent to maximize the overall team's utility, using all available information. We tested our approach extensively in simulations against baselines, and in robustness and ablation studies. In addition, we performed experiments in a 3D physics based engine robot simulator to test the applicability in the real world, as well as with real-world trajectories obtained from an oceanography computational fluid dynamics simulator. Results show the effectiveness of our method, which achieves mission completion times 1.3 to 3.2 times faster in finding all targets, even under the most challenging scenarios where the number of targets is 5 times greater than that of the agents.

Belief Updating by Enumerating High-Probability Independence-Based Assignments

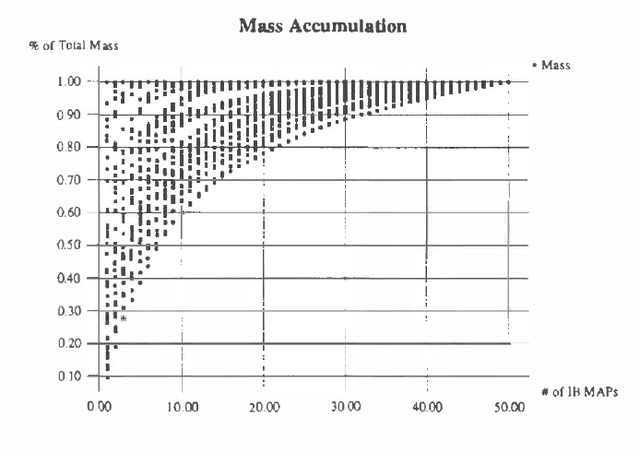
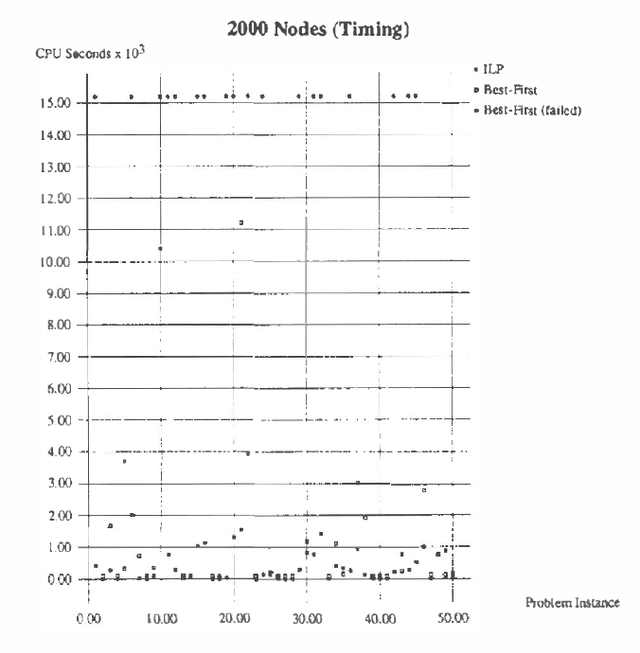
Independence-based (IB) assignments to Bayesian belief networks were originally proposed as abductive explanations. IB assignments assign fewer variables in abductive explanations than do schemes assigning values to all evidentially supported variables. We use IB assignments to approximate marginal probabilities in Bayesian belief networks. Recent work in belief updating for Bayes networks attempts to approximate posterior probabilities by finding a small number of the highest probability complete (or perhaps evidentially supported) assignments. Under certain assumptions, the probability mass in the union of these assignments is sufficient to obtain a good approximation. Such methods are especially useful for highly-connected networks, where the maximum clique size or the cutset size make the standard algorithms intractable. Since IB assignments contain fewer assigned variables, the probability mass in each assignment is greater than in the respective complete assignment. Thus, fewer IB assignments are sufficient, and a good approximation can be obtained more efficiently. IB assignments can be used for efficiently approximating posterior node probabilities even in cases which do not obey the rather strict skewness assumptions used in previous research. Two algorithms for finding the high probability IB assignments are suggested: one by doing a best-first heuristic search, and another by special-purpose integer linear programming. Experimental results show that this approach is feasible for highly connected belief networks.

Sample-and-Accumulate Algorithms for Belief Updating in Bayes Networks

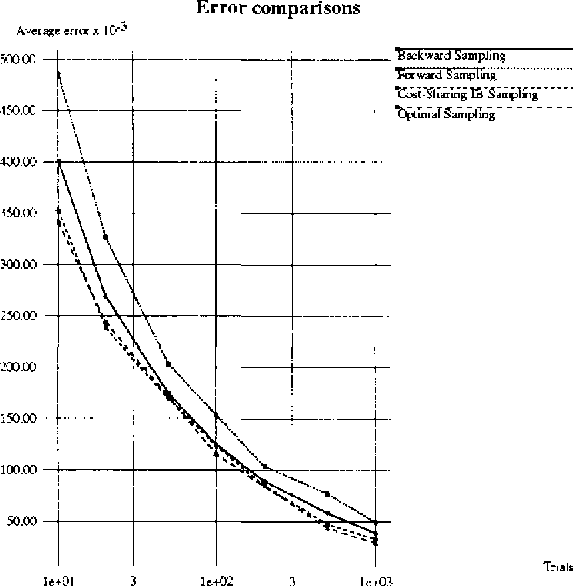
Belief updating in Bayes nets, a well known computationally hard problem, has recently been approximated by several deterministic algorithms, and by various randomized approximation algorithms. Deterministic algorithms usually provide probability bounds, but have an exponential runtime. Some randomized schemes have a polynomial runtime, but provide only probability estimates. We present randomized algorithms that enumerate high-probability partial instantiations, resulting in probability bounds. Some of these algorithms are also sampling algorithms. Specifically, we introduce and evaluate a variant of backward sampling, both as a sampling algorithm and as a randomized enumeration algorithm. We also relax the implicit assumption used by both sampling and accumulation algorithms, that query nodes must be instantiated in all the samples.