Sample-and-Accumulate Algorithms for Belief Updating in Bayes Networks
Paper and Code
Feb 13, 2013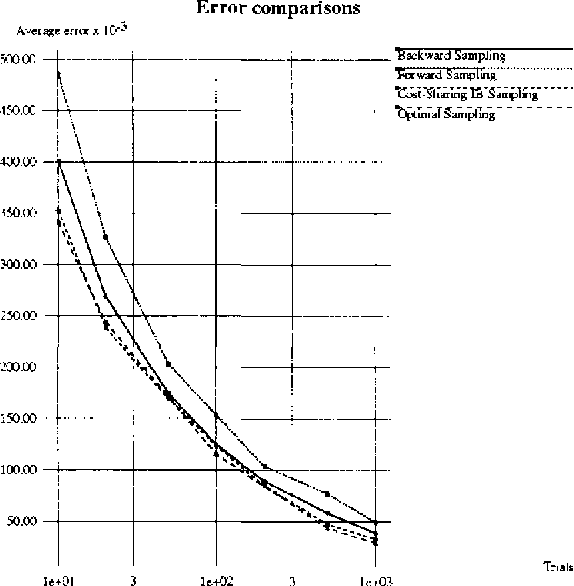
Belief updating in Bayes nets, a well known computationally hard problem, has recently been approximated by several deterministic algorithms, and by various randomized approximation algorithms. Deterministic algorithms usually provide probability bounds, but have an exponential runtime. Some randomized schemes have a polynomial runtime, but provide only probability estimates. We present randomized algorithms that enumerate high-probability partial instantiations, resulting in probability bounds. Some of these algorithms are also sampling algorithms. Specifically, we introduce and evaluate a variant of backward sampling, both as a sampling algorithm and as a randomized enumeration algorithm. We also relax the implicit assumption used by both sampling and accumulation algorithms, that query nodes must be instantiated in all the samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge