AIAuditTrack: A Framework for AI Security system

The rapid expansion of AI-driven applications powered by large language models has led to a surge in AI interaction data, raising urgent challenges in security, accountability, and risk traceability. This paper presents AiAuditTrack (AAT), a blockchain-based framework for AI usage traffic recording and governance. AAT leverages decentralized identity (DID) and verifiable credentials (VC) to establish trusted and identifiable AI entities, and records inter-entity interaction trajectories on-chain to enable cross-system supervision and auditing. AI entities are modeled as nodes in a dynamic interaction graph, where edges represent time-specific behavioral trajectories. Based on this model, a risk diffusion algorithm is proposed to trace the origin of risky behaviors and propagate early warnings across involved entities. System performance is evaluated using blockchain Transactions Per Second (TPS) metrics, demonstrating the feasibility and stability of AAT under large-scale interaction recording. AAT provides a scalable and verifiable solution for AI auditing, risk management, and responsibility attribution in complex multi-agent environments.

Tree-Based Stochastic Optimization for Solving Large-Scale Urban Network Security Games

Urban Network Security Games (UNSGs), which model the strategic allocation of limited security resources on city road networks, are critical for urban safety. However, finding a Nash Equilibrium (NE) in large-scale UNSGs is challenging due to their massive and combinatorial action spaces. One common approach to addressing these games is the Policy-Space Response Oracle (PSRO) framework, which requires computing best responses (BR) at each iteration. However, precisely computing exact BRs is impractical in large-scale games, and employing reinforcement learning to approximate BRs inevitably introduces errors, which limits the overall effectiveness of the PSRO methods. Recent advancements in leveraging non-convex stochastic optimization to approximate an NE offer a promising alternative to the burdensome BR computation. However, utilizing existing stochastic optimization techniques with an unbiased loss function for UNSGs remains challenging because the action spaces are too vast to be effectively represented by neural networks. To address these issues, we introduce Tree-based Stochastic Optimization (TSO), a framework that bridges the gap between the stochastic optimization paradigm for NE-finding and the demands of UNSGs. Specifically, we employ the tree-based action representation that maps the whole action space onto a tree structure, addressing the challenge faced by neural networks in representing actions when the action space cannot be enumerated. We then incorporate this representation into the loss function and theoretically demonstrate its equivalence to the unbiased loss function. To further enhance the quality of the converged solution, we introduce a sample-and-prune mechanism that reduces the risk of being trapped in suboptimal local optima. Extensive experimental results indicate the superiority of TSO over other baseline algorithms in addressing the UNSGs.

The Docking Game: Loop Self-Play for Fast, Dynamic, and Accurate Prediction of Flexible Protein--Ligand Binding

Molecular docking is a crucial aspect of drug discovery, as it predicts the binding interactions between small-molecule ligands and protein pockets. However, current multi-task learning models for docking often show inferior performance in ligand docking compared to protein pocket docking. This disparity arises largely due to the distinct structural complexities of ligands and proteins. To address this issue, we propose a novel game-theoretic framework that models the protein-ligand interaction as a two-player game called the Docking Game, with the ligand docking module acting as the ligand player and the protein pocket docking module as the protein player. To solve this game, we develop a novel Loop Self-Play (LoopPlay) algorithm, which alternately trains these players through a two-level loop. In the outer loop, the players exchange predicted poses, allowing each to incorporate the other's structural predictions, which fosters mutual adaptation over multiple iterations. In the inner loop, each player dynamically refines its predictions by incorporating its own predicted ligand or pocket poses back into its model. We theoretically show the convergence of LoopPlay, ensuring stable optimization. Extensive experiments conducted on public benchmark datasets demonstrate that LoopPlay achieves approximately a 10\% improvement in predicting accurate binding modes compared to previous state-of-the-art methods. This highlights its potential to enhance the accuracy of molecular docking in drug discovery.

Asynchronous Predictive Counterfactual Regret Minimization$^+$ Algorithm in Solving Extensive-Form Games

Counterfactual Regret Minimization (CFR) algorithms are widely used to compute a Nash equilibrium (NE) in two-player zero-sum imperfect-information extensive-form games (IIGs). Among them, Predictive CFR$^+$ (PCFR$^+$) is particularly powerful, achieving an exceptionally fast empirical convergence rate via the prediction in many games. However, the empirical convergence rate of PCFR$^+$ would significantly degrade if the prediction is inaccurate, leading to unstable performance on certain IIGs. To enhance the robustness of PCFR$^+$, we propose a novel variant, Asynchronous PCFR$^+$ (APCFR$^+$), which employs an adaptive asynchronization of step-sizes between the updates of implicit and explicit accumulated counterfactual regrets to mitigate the impact of the prediction inaccuracy on convergence. We present a theoretical analysis demonstrating why APCFR$^+$ can enhance the robustness. Finally, we propose a simplified version of APCFR$^+$ called Simple APCFR$^+$ (SAPCFR$^+$), which uses a fixed asynchronization of step-sizes to simplify the implementation that only needs a single-line modification of the original PCFR+. Interestingly, SAPCFR$^+$ achieves a constant-factor lower theoretical regret bound than PCFR$^+$ in the worst case. Experimental results demonstrate that (i) both APCFR$^+$ and SAPCFR$^+$ outperform PCFR$^+$ in most of the tested games, as well as (ii) SAPCFR$^+$ achieves a comparable empirical convergence rate with APCFR$^+$.

Multi-Object Active Search and Tracking by Multiple Agents in Untrusted, Dynamically Changing Environments

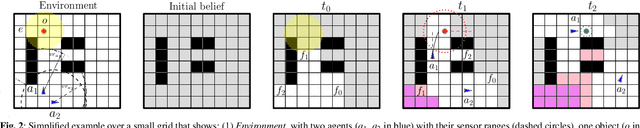
This paper addresses the problem of both actively searching and tracking multiple unknown dynamic objects in a known environment with multiple cooperative autonomous agents with partial observability. The tracking of a target ends when the uncertainty is below a threshold. Current methods typically assume homogeneous agents without access to external information and utilize short-horizon target predictive models. Such assumptions limit real-world applications. We propose a fully integrated pipeline where the main contributions are: (1) a time-varying weighted belief representation capable of handling knowledge that changes over time, which includes external reports of varying levels of trustworthiness in addition to the agents; (2) the integration of a Long Short Term Memory-based trajectory prediction within the optimization framework for long-horizon decision-making, which reasons in time-configuration space, thus increasing responsiveness; and (3) a comprehensive system that accounts for multiple agents and enables information-driven optimization. When communication is available, our strategy consolidates exploration results collected asynchronously by agents and external sources into a headquarters, who can allocate each agent to maximize the overall team's utility, using all available information. We tested our approach extensively in simulations against baselines, and in robustness and ablation studies. In addition, we performed experiments in a 3D physics based engine robot simulator to test the applicability in the real world, as well as with real-world trajectories obtained from an oceanography computational fluid dynamics simulator. Results show the effectiveness of our method, which achieves mission completion times 1.3 to 3.2 times faster in finding all targets, even under the most challenging scenarios where the number of targets is 5 times greater than that of the agents.

Solving Urban Network Security Games: Learning Platform, Benchmark, and Challenge for AI Research

After the great achievement of solving two-player zero-sum games, more and more AI researchers focus on solving multiplayer games. To facilitate the development of designing efficient learning algorithms for solving multiplayer games, we propose a multiplayer game platform for solving Urban Network Security Games (\textbf{UNSG}) that model real-world scenarios. That is, preventing criminal activity is a highly significant responsibility assigned to police officers in cities, and police officers have to allocate their limited security resources to interdict the escaping criminal when a crime takes place in a city. This interaction between multiple police officers and the escaping criminal can be modeled as a UNSG. The variants of UNSGs can model different real-world settings, e.g., whether real-time information is available or not, and whether police officers can communicate or not. The main challenges of solving this game include the large size of the game and the co-existence of cooperation and competition. While previous efforts have been made to tackle UNSGs, they have been hampered by performance and scalability issues. Therefore, we propose an open-source UNSG platform (\textbf{GraphChase}) for designing efficient learning algorithms for solving UNSGs. Specifically, GraphChase offers a unified and flexible game environment for modeling various variants of UNSGs, supporting the development, testing, and benchmarking of algorithms. We believe that GraphChase not only facilitates the development of efficient algorithms for solving real-world problems but also paves the way for significant advancements in algorithmic development for solving general multiplayer games.

Siren: A Learning-Based Multi-Turn Attack Framework for Simulating Real-World Human Jailbreak Behaviors

Large language models (LLMs) are widely used in real-world applications, raising concerns about their safety and trustworthiness. While red-teaming with jailbreak prompts exposes the vulnerabilities of LLMs, current efforts focus primarily on single-turn attacks, overlooking the multi-turn strategies used by real-world adversaries. Existing multi-turn methods rely on static patterns or predefined logical chains, failing to account for the dynamic strategies during attacks. We propose Siren, a learning-based multi-turn attack framework designed to simulate real-world human jailbreak behaviors. Siren consists of three stages: (1) training set construction utilizing Turn-Level LLM feedback (Turn-MF), (2) post-training attackers with supervised fine-tuning (SFT) and direct preference optimization (DPO), and (3) interactions between the attacking and target LLMs. Experiments demonstrate that Siren achieves an attack success rate (ASR) of 90% with LLaMA-3-8B as the attacker against Gemini-1.5-Pro as the target model, and 70% with Mistral-7B against GPT-4o, significantly outperforming single-turn baselines. Moreover, Siren with a 7B-scale model achieves performance comparable to a multi-turn baseline that leverages GPT-4o as the attacker, while requiring fewer turns and employing decomposition strategies that are better semantically aligned with attack goals. We hope Siren inspires the development of stronger defenses against advanced multi-turn jailbreak attacks under realistic scenarios. Code is available at https://github.com/YiyiyiZhao/siren. Warning: This paper contains potentially harmful text.

Computing Ex Ante Equilibrium in Heterogeneous Zero-Sum Team Games

The ex ante equilibrium for two-team zero-sum games, where agents within each team collaborate to compete against the opposing team, is known to be the best a team can do for coordination. Many existing works on ex ante equilibrium solutions are aiming to extend the scope of ex ante equilibrium solving to large-scale team games based on Policy Space Response Oracle (PSRO). However, the joint team policy space constructed by the most prominent method, Team PSRO, cannot cover the entire team policy space in heterogeneous team games where teammates play distinct roles. Such insufficient policy expressiveness causes Team PSRO to be trapped into a sub-optimal ex ante equilibrium with significantly higher exploitability and never converges to the global ex ante equilibrium. To find the global ex ante equilibrium without introducing additional computational complexity, we first parameterize heterogeneous policies for teammates, and we prove that optimizing the heterogeneous teammates' policies sequentially can guarantee a monotonic improvement in team rewards. We further propose Heterogeneous-PSRO (H-PSRO), a novel framework for heterogeneous team games, which integrates the sequential correlation mechanism into the PSRO framework and serves as the first PSRO framework for heterogeneous team games. We prove that H-PSRO achieves lower exploitability than Team PSRO in heterogeneous team games. Empirically, H-PSRO achieves convergence in matrix heterogeneous games that are unsolvable by non-heterogeneous baselines. Further experiments reveal that H-PSRO outperforms non-heterogeneous baselines in both heterogeneous team games and homogeneous settings.

Tailed Low-Rank Matrix Factorization for Similarity Matrix Completion

Similarity matrix serves as a fundamental tool at the core of numerous downstream machine-learning tasks. However, missing data is inevitable and often results in an inaccurate similarity matrix. To address this issue, Similarity Matrix Completion (SMC) methods have been proposed, but they suffer from high computation complexity due to the Singular Value Decomposition (SVD) operation. To reduce the computation complexity, Matrix Factorization (MF) techniques are more explicit and frequently applied to provide a low-rank solution, but the exact low-rank optimal solution can not be guaranteed since it suffers from a non-convex structure. In this paper, we introduce a novel SMC framework that offers a more reliable and efficient solution. Specifically, beyond simply utilizing the unique Positive Semi-definiteness (PSD) property to guide the completion process, our approach further complements a carefully designed rank-minimization regularizer, aiming to achieve an optimal and low-rank solution. Based on the key insights that the underlying PSD property and Low-Rank property improve the SMC performance, we present two novel, scalable, and effective algorithms, SMCNN and SMCNmF, which investigate the PSD property to guide the estimation process and incorporate nonconvex low-rank regularizer to ensure the low-rank solution. Theoretical analysis ensures better estimation performance and convergence speed. Empirical results on real-world datasets demonstrate the superiority and efficiency of our proposed methods compared to various baseline methods.

In-Context Exploiter for Extensive-Form Games

Nash equilibrium (NE) is a widely adopted solution concept in game theory due to its stability property. However, we observe that the NE strategy might not always yield the best results, especially against opponents who do not adhere to NE strategies. Based on this observation, we pose a new game-solving question: Can we learn a model that can exploit any, even NE, opponent to maximize their own utility? In this work, we make the first attempt to investigate this problem through in-context learning. Specifically, we introduce a novel method, In-Context Exploiter (ICE), to train a single model that can act as any player in the game and adaptively exploit opponents entirely by in-context learning. Our ICE algorithm involves generating diverse opponent strategies, collecting interactive history training data by a reinforcement learning algorithm, and training a transformer-based agent within a well-designed curriculum learning framework. Finally, comprehensive experimental results validate the effectiveness of our ICE algorithm, showcasing its in-context learning ability to exploit any unknown opponent, thereby positively answering our initial game-solving question.