In-Context Exploiter for Extensive-Form Games

Nash equilibrium (NE) is a widely adopted solution concept in game theory due to its stability property. However, we observe that the NE strategy might not always yield the best results, especially against opponents who do not adhere to NE strategies. Based on this observation, we pose a new game-solving question: Can we learn a model that can exploit any, even NE, opponent to maximize their own utility? In this work, we make the first attempt to investigate this problem through in-context learning. Specifically, we introduce a novel method, In-Context Exploiter (ICE), to train a single model that can act as any player in the game and adaptively exploit opponents entirely by in-context learning. Our ICE algorithm involves generating diverse opponent strategies, collecting interactive history training data by a reinforcement learning algorithm, and training a transformer-based agent within a well-designed curriculum learning framework. Finally, comprehensive experimental results validate the effectiveness of our ICE algorithm, showcasing its in-context learning ability to exploit any unknown opponent, thereby positively answering our initial game-solving question.

Configurable Mirror Descent: Towards a Unification of Decision Making

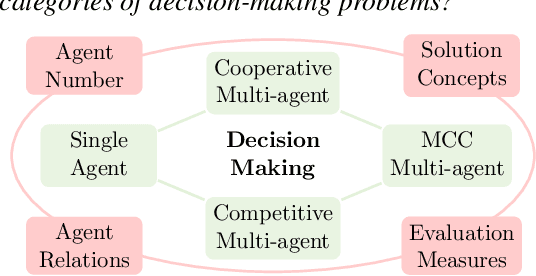
Decision-making problems, categorized as single-agent, e.g., Atari, cooperative multi-agent, e.g., Hanabi, competitive multi-agent, e.g., Hold'em poker, and mixed cooperative and competitive, e.g., football, are ubiquitous in the real world. Various methods are proposed to address the specific decision-making problems. Despite the successes in specific categories, these methods typically evolve independently and cannot generalize to other categories. Therefore, a fundamental question for decision-making is: \emph{Can we develop \textbf{a single algorithm} to tackle \textbf{ALL} categories of decision-making problems?} There are several main challenges to address this question: i) different decision-making categories involve different numbers of agents and different relationships between agents, ii) different categories have different solution concepts and evaluation measures, and iii) there lacks a comprehensive benchmark covering all the categories. This work presents a preliminary attempt to address the question with three main contributions. i) We propose the generalized mirror descent (GMD), a generalization of MD variants, which considers multiple historical policies and works with a broader class of Bregman divergences. ii) We propose the configurable mirror descent (CMD) where a meta-controller is introduced to dynamically adjust the hyper-parameters in GMD conditional on the evaluation measures. iii) We construct the \textsc{GameBench} with 15 academic-friendly games across different decision-making categories. Extensive experiments demonstrate that CMD achieves empirically competitive or better outcomes compared to baselines while providing the capability of exploring diverse dimensions of decision making.

Grasper: A Generalist Pursuer for Pursuit-Evasion Problems

Pursuit-evasion games (PEGs) model interactions between a team of pursuers and an evader in graph-based environments such as urban street networks. Recent advancements have demonstrated the effectiveness of the pre-training and fine-tuning paradigm in PSRO to improve scalability in solving large-scale PEGs. However, these methods primarily focus on specific PEGs with fixed initial conditions that may vary substantially in real-world scenarios, which significantly hinders the applicability of the traditional methods. To address this issue, we introduce Grasper, a GeneRAlist purSuer for Pursuit-Evasion pRoblems, capable of efficiently generating pursuer policies tailored to specific PEGs. Our contributions are threefold: First, we present a novel architecture that offers high-quality solutions for diverse PEGs, comprising critical components such as (i) a graph neural network (GNN) to encode PEGs into hidden vectors, and (ii) a hypernetwork to generate pursuer policies based on these hidden vectors. As a second contribution, we develop an efficient three-stage training method involving (i) a pre-pretraining stage for learning robust PEG representations through self-supervised graph learning techniques like GraphMAE, (ii) a pre-training stage utilizing heuristic-guided multi-task pre-training (HMP) where heuristic-derived reference policies (e.g., through Dijkstra's algorithm) regularize pursuer policies, and (iii) a fine-tuning stage that employs PSRO to generate pursuer policies on designated PEGs. Finally, we perform extensive experiments on synthetic and real-world maps, showcasing Grasper's significant superiority over baselines in terms of solution quality and generalizability. We demonstrate that Grasper provides a versatile approach for solving pursuit-evasion problems across a broad range of scenarios, enabling practical deployment in real-world situations.

Self-adaptive PSRO: Towards an Automatic Population-based Game Solver

Policy-Space Response Oracles (PSRO) as a general algorithmic framework has achieved state-of-the-art performance in learning equilibrium policies of two-player zero-sum games. However, the hand-crafted hyperparameter value selection in most of the existing works requires extensive domain knowledge, forming the main barrier to applying PSRO to different games. In this work, we make the first attempt to investigate the possibility of self-adaptively determining the optimal hyperparameter values in the PSRO framework. Our contributions are three-fold: (1) Using several hyperparameters, we propose a parametric PSRO that unifies the gradient descent ascent (GDA) and different PSRO variants. (2) We propose the self-adaptive PSRO (SPSRO) by casting the hyperparameter value selection of the parametric PSRO as a hyperparameter optimization (HPO) problem where our objective is to learn an HPO policy that can self-adaptively determine the optimal hyperparameter values during the running of the parametric PSRO. (3) To overcome the poor performance of online HPO methods, we propose a novel offline HPO approach to optimize the HPO policy based on the Transformer architecture. Experiments on various two-player zero-sum games demonstrate the superiority of SPSRO over different baselines.

Population-size-Aware Policy Optimization for Mean-Field Games

In this work, we attempt to bridge the two fields of finite-agent and infinite-agent games, by studying how the optimal policies of agents evolve with the number of agents (population size) in mean-field games, an agent-centric perspective in contrast to the existing works focusing typically on the convergence of the empirical distribution of the population. To this end, the premise is to obtain the optimal policies of a set of finite-agent games with different population sizes. However, either deriving the closed-form solution for each game is theoretically intractable, training a distinct policy for each game is computationally intensive, or directly applying the policy trained in a game to other games is sub-optimal. We address these challenges through the Population-size-Aware Policy Optimization (PAPO). Our contributions are three-fold. First, to efficiently generate efficient policies for games with different population sizes, we propose PAPO, which unifies two natural options (augmentation and hypernetwork) and achieves significantly better performance. PAPO consists of three components: i) the population-size encoding which transforms the original value of population size to an equivalent encoding to avoid training collapse, ii) a hypernetwork to generate a distinct policy for each game conditioned on the population size, and iii) the population size as an additional input to the generated policy. Next, we construct a multi-task-based training procedure to efficiently train the neural networks of PAPO by sampling data from multiple games with different population sizes. Finally, extensive experiments on multiple environments show the significant superiority of PAPO over baselines, and the analysis of the evolution of the generated policies further deepens our understanding of the two fields of finite-agent and infinite-agent games.