VS Subrahmanian
Strategic Communication under Threat: Learning Information Trade-offs in Pursuit-Evasion Games
Oct 09, 2025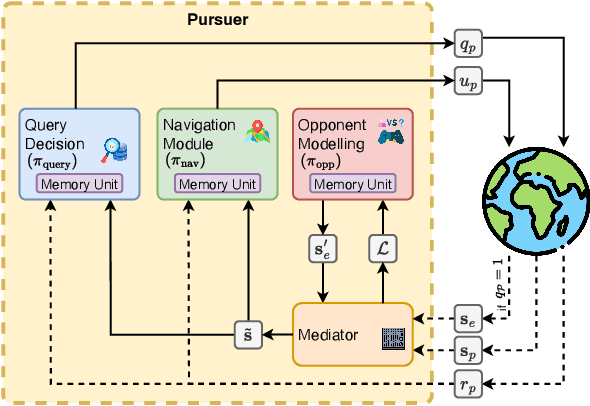
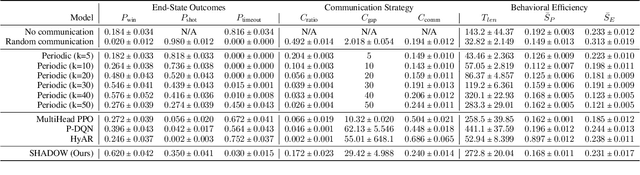
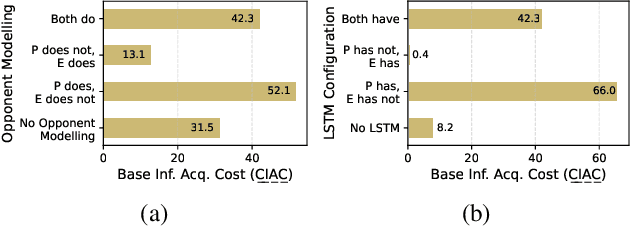
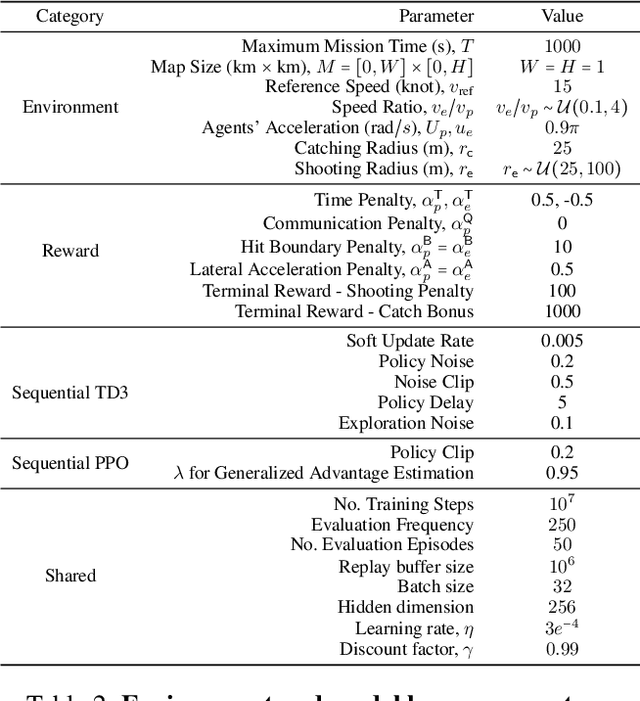
Abstract:Adversarial environments require agents to navigate a key strategic trade-off: acquiring information enhances situational awareness, but may simultaneously expose them to threats. To investigate this tension, we formulate a PursuitEvasion-Exposure-Concealment Game (PEEC) in which a pursuer agent must decide when to communicate in order to obtain the evader's position. Each communication reveals the pursuer's location, increasing the risk of being targeted. Both agents learn their movement policies via reinforcement learning, while the pursuer additionally learns a communication policy that balances observability and risk. We propose SHADOW (Strategic-communication Hybrid Action Decision-making under partial Observation for Warfare), a multi-headed sequential reinforcement learning framework that integrates continuous navigation control, discrete communication actions, and opponent modeling for behavior prediction. Empirical evaluations show that SHADOW pursuers achieve higher success rates than six competitive baselines. Our ablation study confirms that temporal sequence modeling and opponent modeling are critical for effective decision-making. Finally, our sensitivity analysis reveals that the learned policies generalize well across varying communication risks and physical asymmetries between agents.
Multi-Object Active Search and Tracking by Multiple Agents in Untrusted, Dynamically Changing Environments
Feb 03, 2025

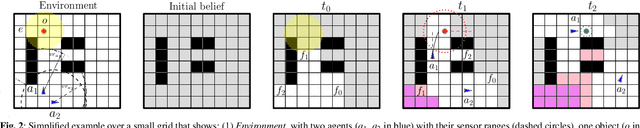

Abstract:This paper addresses the problem of both actively searching and tracking multiple unknown dynamic objects in a known environment with multiple cooperative autonomous agents with partial observability. The tracking of a target ends when the uncertainty is below a threshold. Current methods typically assume homogeneous agents without access to external information and utilize short-horizon target predictive models. Such assumptions limit real-world applications. We propose a fully integrated pipeline where the main contributions are: (1) a time-varying weighted belief representation capable of handling knowledge that changes over time, which includes external reports of varying levels of trustworthiness in addition to the agents; (2) the integration of a Long Short Term Memory-based trajectory prediction within the optimization framework for long-horizon decision-making, which reasons in time-configuration space, thus increasing responsiveness; and (3) a comprehensive system that accounts for multiple agents and enables information-driven optimization. When communication is available, our strategy consolidates exploration results collected asynchronously by agents and external sources into a headquarters, who can allocate each agent to maximize the overall team's utility, using all available information. We tested our approach extensively in simulations against baselines, and in robustness and ablation studies. In addition, we performed experiments in a 3D physics based engine robot simulator to test the applicability in the real world, as well as with real-world trajectories obtained from an oceanography computational fluid dynamics simulator. Results show the effectiveness of our method, which achieves mission completion times 1.3 to 3.2 times faster in finding all targets, even under the most challenging scenarios where the number of targets is 5 times greater than that of the agents.
Higher Layers Need More LoRA Experts
Feb 13, 2024



Abstract:Parameter-efficient tuning (PEFT) techniques like low-rank adaptation (LoRA) offer training efficiency on Large Language Models, but their impact on model performance remains limited. Recent efforts integrate LoRA and Mixture-of-Experts (MoE) to improve the performance of PEFT methods. Despite promising results, research on improving the efficiency of LoRA with MoE is still in its early stages. Recent studies have shown that experts in the MoE architecture have different strengths and also exhibit some redundancy. Does this statement also apply to parameter-efficient MoE? In this paper, we introduce a novel parameter-efficient MoE method, \textit{\textbf{M}oE-L\textbf{o}RA with \textbf{L}ayer-wise Expert \textbf{A}llocation (MoLA)} for Transformer-based models, where each model layer has the flexibility to employ a varying number of LoRA experts. We investigate several architectures with varying layer-wise expert configurations. Experiments on six well-known NLP and commonsense QA benchmarks demonstrate that MoLA achieves equal or superior performance compared to all baselines. We find that allocating more LoRA experts to higher layers further enhances the effectiveness of models with a certain number of experts in total. With much fewer parameters, this allocation strategy outperforms the setting with the same number of experts in every layer. This work can be widely used as a plug-and-play parameter-efficient tuning approach for various applications. The code is available at https://github.com/GCYZSL/MoLA.
Improving Performance of heavily loaded agents
Dec 11, 2000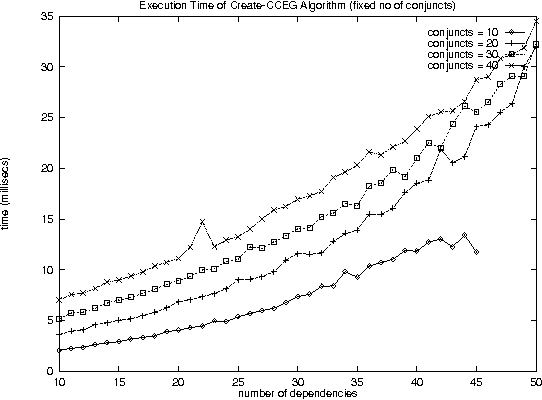
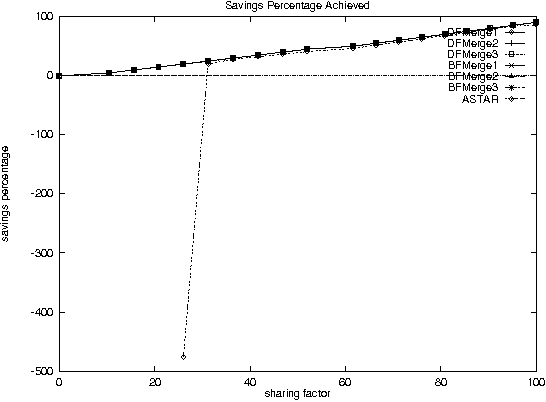
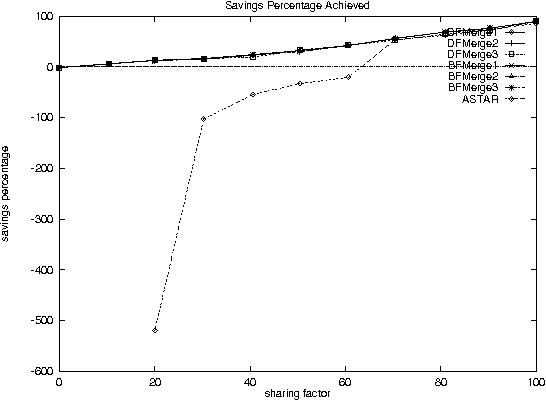
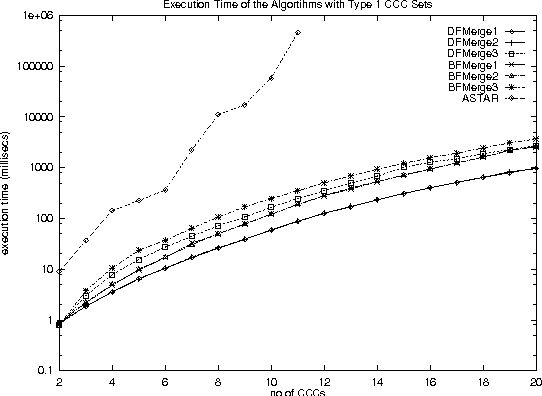
Abstract:With the increase in agent-based applications, there are now agent systems that support \emph{concurrent} client accesses. The ability to process large volumes of simultaneous requests is critical in many such applications. In such a setting, the traditional approach of serving these requests one at a time via queues (e.g. \textsf{FIFO} queues, priority queues) is insufficient. Alternative models are essential to improve the performance of such \emph{heavily loaded} agents. In this paper, we propose a set of \emph{cost-based algorithms} to \emph{optimize} and \emph{merge} multiple requests submitted to an agent. In order to merge a set of requests, one first needs to identify commonalities among such requests. First, we provide an \emph{application independent framework} within which an agent developer may specify relationships (called \emph{invariants}) between requests. Second, we provide two algorithms (and various accompanying heuristics) which allow an agent to automatically rewrite requests so as to avoid redundant work---these algorithms take invariants associated with the agent into account. Our algorithms are independent of any specific agent framework. For an implementation, we implemented both these algorithms on top of the \impact agent development platform, and on top of a (non-\impact) geographic database agent. Based on these implementations, we conducted experiments and show that our algorithms are considerably more efficient than methods that use the $A^*$ algorithm.
Probabilistic Agent Programs
Oct 21, 1999
Abstract:Agents are small programs that autonomously take actions based on changes in their environment or ``state.'' Over the last few years, there have been an increasing number of efforts to build agents that can interact and/or collaborate with other agents. In one of these efforts, Eiter, Subrahmanian amd Pick (AIJ, 108(1-2), pages 179-255) have shown how agents may be built on top of legacy code. However, their framework assumes that agent states are completely determined, and there is no uncertainty in an agent's state. Thus, their framework allows an agent developer to specify how his agents will react when the agent is 100% sure about what is true/false in the world state. In this paper, we propose the concept of a \emph{probabilistic agent program} and show how, given an arbitrary program written in any imperative language, we may build a declarative ``probabilistic'' agent program on top of it which supports decision making in the presence of uncertainty. We provide two alternative semantics for probabilistic agent programs. We show that the second semantics, though more epistemically appealing, is more complex to compute. We provide sound and complete algorithms to compute the semantics of \emph{positive} agent programs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge