Towards Rational Deployment of Multiple Heuristics in A*
Paper and Code
May 22, 2013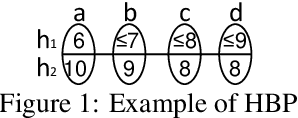
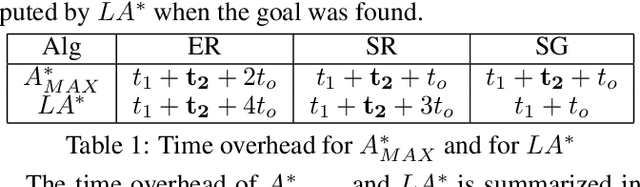
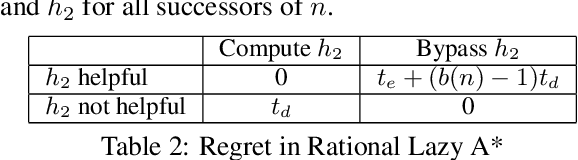

The obvious way to use several admissible heuristics in A* is to take their maximum. In this paper we aim to reduce the time spent on computing heuristics. We discuss Lazy A*, a variant of A* where heuristics are evaluated lazily: only when they are essential to a decision to be made in the A* search process. We present a new rational meta-reasoning based scheme, rational lazy A*, which decides whether to compute the more expensive heuristics at all, based on a myopic value of information estimate. Both methods are examined theoretically. Empirical evaluation on several domains supports the theoretical results, and shows that lazy A* and rational lazy A* are state-of-the-art heuristic combination methods.
* 7 pages, IJCAI 2013, to appear
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge