Learning with Local Search MCMC Layers

Integrating combinatorial optimization layers into neural networks has recently attracted significant research interest. However, many existing approaches lack theoretical guarantees or fail to perform adequately when relying on inexact solvers. This is a critical limitation, as many operations research problems are NP-hard, often necessitating the use of neighborhood-based local search heuristics. These heuristics iteratively generate and evaluate candidate solutions based on an acceptance rule. In this paper, we introduce a theoretically-principled approach for learning with such inexact combinatorial solvers. Inspired by the connection between simulated annealing and Metropolis-Hastings, we propose to transform problem-specific neighborhood systems used in local search heuristics into proposal distributions, implementing MCMC on the combinatorial space of feasible solutions. This allows us to construct differentiable combinatorial layers and associated loss functions. Replacing an exact solver by a local search strongly reduces the computational burden of learning on many applications. We demonstrate our approach on a large-scale dynamic vehicle routing problem with time windows.

Primal-dual algorithm for contextual stochastic combinatorial optimization

This paper introduces a novel approach to contextual stochastic optimization, integrating operations research and machine learning to address decision-making under uncertainty. Traditional methods often fail to leverage contextual information, which underscores the necessity for new algorithms. In this study, we utilize neural networks with combinatorial optimization layers to encode policies. Our goal is to minimize the empirical risk, which is estimated from past data on uncertain parameters and contexts. To that end, we present a surrogate learning problem and a generic primal-dual algorithm that is applicable to various combinatorial settings in stochastic optimization. Our approach extends classic Fenchel-Young loss results and introduces a new regularization method using sparse perturbations on the distribution simplex. This allows for tractable updates in the original space and can accommodate diverse objective functions. We demonstrate the linear convergence of our algorithm under certain conditions and provide a bound on the non-optimality of the resulting policy in terms of the empirical risk. Experiments on a contextual stochastic minimum weight spanning tree problem show that our algorithm is efficient and scalable, achieving performance comparable to imitation learning of solutions computed using an expensive Lagrangian-based heuristic.

Preference-aware compensation policies for crowdsourced on-demand services

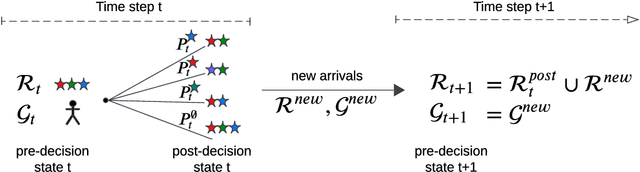
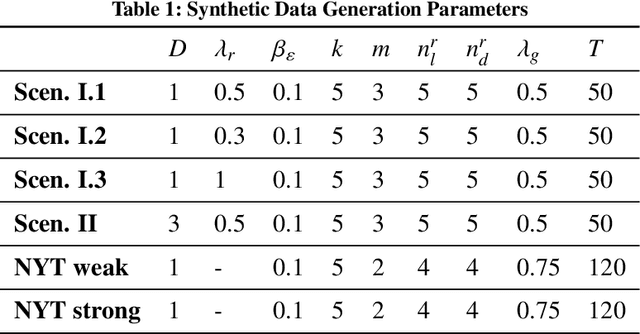
Crowdsourced on-demand services offer benefits such as reduced costs, faster service fulfillment times, greater adaptability, and contributions to sustainable urban transportation in on-demand delivery contexts. However, the success of an on-demand platform that utilizes crowdsourcing relies on finding a compensation policy that strikes a balance between creating attractive offers for gig workers and ensuring profitability. In this work, we examine a dynamic pricing problem for an on-demand platform that sets request-specific compensation of gig workers in a discrete-time framework, where requests and workers arrive stochastically. The operator's goal is to determine a compensation policy that maximizes the total expected reward over the time horizon. Our approach introduces compensation strategies that explicitly account for gig worker request preferences. To achieve this, we employ the Multinomial Logit model to represent the acceptance probabilities of gig workers, and, as a result, derive an analytical solution that utilizes post-decision states. Subsequently, we integrate this solution into an approximate dynamic programming algorithm. We compare our algorithm against benchmark algorithms, including formula-based policies and an upper bound provided by the full information linear programming solution. Our algorithm demonstrates consistent performance across diverse settings, achieving improvements of at least 2.5-7.5% in homogeneous gig worker populations and 9% in heterogeneous populations over benchmarks, based on fully synthetic data. For real-world data, it surpasses benchmarks by 8% in weak and 20% in strong location preference scenarios.

DistrictNet: Decision-aware learning for geographical districting

Districting is a complex combinatorial problem that consists in partitioning a geographical area into small districts. In logistics, it is a major strategic decision determining operating costs for several years. Solving districting problems using traditional methods is intractable even for small geographical areas and existing heuristics often provide sub-optimal results. We present a structured learning approach to find high-quality solutions to real-world districting problems in a few minutes. It is based on integrating a combinatorial optimization layer, the capacitated minimum spanning tree problem, into a graph neural network architecture. To train this pipeline in a decision-aware fashion, we show how to construct target solutions embedded in a suitable space and learn from target solutions. Experiments show that our approach outperforms existing methods as it can significantly reduce costs on real-world cities.

WardropNet: Traffic Flow Predictions via Equilibrium-Augmented Learning

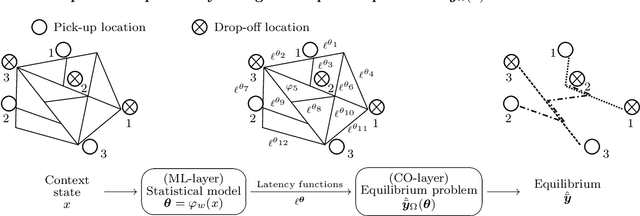
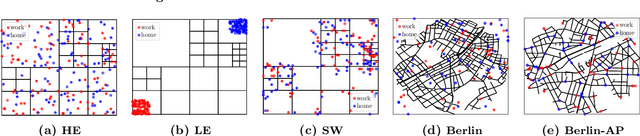
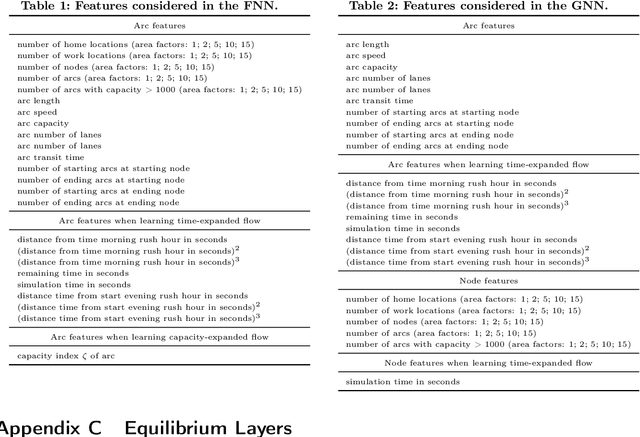
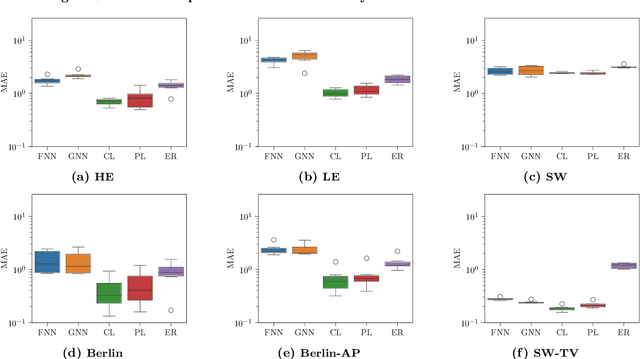
When optimizing transportation systems, anticipating traffic flows is a central element. Yet, computing such traffic equilibria remains computationally expensive. Against this background, we introduce a novel combinatorial optimization augmented neural network architecture that allows for fast and accurate traffic flow predictions. We propose WardropNet, a neural network that combines classical layers with a subsequent equilibrium layer: the first ones inform the latter by predicting the parameterization of the equilibrium problem's latency functions. Using supervised learning we minimize the difference between the actual traffic flow and the predicted output. We show how to leverage a Bregman divergence fitting the geometry of the equilibria, which allows for end-to-end learning. WardropNet outperforms pure learning-based approaches in predicting traffic equilibria for realistic and stylized traffic scenarios. On realistic scenarios, WardropNet improves on average for time-invariant predictions by up to 72% and for time-variant predictions by up to 23% over pure learning-based approaches.

Generalization Bounds of Surrogate Policies for Combinatorial Optimization Problems

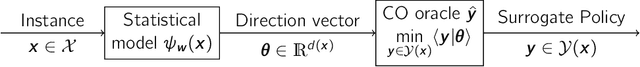
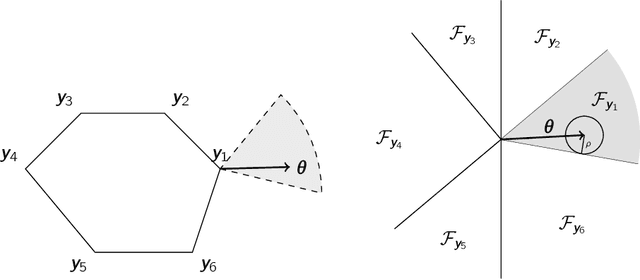
A recent stream of structured learning approaches has improved the practical state of the art for a range of combinatorial optimization problems with complex objectives encountered in operations research. Such approaches train policies that chain a statistical model with a surrogate combinatorial optimization oracle to map any instance of the problem to a feasible solution. The key idea is to exploit the statistical distribution over instances instead of dealing with instances separately. However learning such policies by risk minimization is challenging because the empirical risk is piecewise constant in the parameters, and few theoretical guarantees have been provided so far. In this article, we investigate methods that smooth the risk by perturbing the policy, which eases optimization and improves generalization. Our main contribution is a generalization bound that controls the perturbation bias, the statistical learning error, and the optimization error. Our analysis relies on the introduction of a uniform weak property, which captures and quantifies the interplay of the statistical model and the surrogate combinatorial optimization oracle. This property holds under mild assumptions on the statistical model, the surrogate optimization, and the instance data distribution. We illustrate the result on a range of applications such as stochastic vehicle scheduling. In particular, such policies are relevant for contextual stochastic optimization and our results cover this case.

CF-OPT: Counterfactual Explanations for Structured Prediction

Optimization layers in deep neural networks have enjoyed a growing popularity in structured learning, improving the state of the art on a variety of applications. Yet, these pipelines lack interpretability since they are made of two opaque layers: a highly non-linear prediction model, such as a deep neural network, and an optimization layer, which is typically a complex black-box solver. Our goal is to improve the transparency of such methods by providing counterfactual explanations. We build upon variational autoencoders a principled way of obtaining counterfactuals: working in the latent space leads to a natural notion of plausibility of explanations. We finally introduce a variant of the classic loss for VAE training that improves their performance in our specific structured context. These provide the foundations of CF-OPT, a first-order optimization algorithm that can find counterfactual explanations for a broad class of structured learning architectures. Our numerical results show that both close and plausible explanations can be obtained for problems from the recent literature.

Predicting Accurate Lagrangian Multipliers for Mixed Integer Linear Programs

Lagrangian relaxation stands among the most efficient approaches for solving a Mixed Integer Linear Programs (MILP) with difficult constraints. Given any duals for these constraints, called Lagrangian Multipliers (LMs), it returns a bound on the optimal value of the MILP, and Lagrangian methods seek the LMs giving the best such bound. But these methods generally rely on iterative algorithms resembling gradient descent to maximize the concave piecewise linear dual function: the computational burden grows quickly with the number of relaxed constraints. We introduce a deep learning approach that bypasses the descent, effectively amortizing the local, per instance, optimization. A probabilistic encoder based on a graph convolutional network computes high-dimensional representations of relaxed constraints in MILP instances. A decoder then turns these representations into LMs. We train the encoder and decoder jointly by directly optimizing the bound obtained from the predicted multipliers. Numerical experiments show that our approach closes up to 85~\% of the gap between the continuous relaxation and the best Lagrangian bound, and provides a high quality warm-start for descent based Lagrangian methods.

Combinatorial Optimization enriched Machine Learning to solve the Dynamic Vehicle Routing Problem with Time Windows

With the rise of e-commerce and increasing customer requirements, logistics service providers face a new complexity in their daily planning, mainly due to efficiently handling same day deliveries. Existing multi-stage stochastic optimization approaches that allow to solve the underlying dynamic vehicle routing problem are either computationally too expensive for an application in online settings, or -- in the case of reinforcement learning -- struggle to perform well on high-dimensional combinatorial problems. To mitigate these drawbacks, we propose a novel machine learning pipeline that incorporates a combinatorial optimization layer. We apply this general pipeline to a dynamic vehicle routing problem with dispatching waves, which was recently promoted in the EURO Meets NeurIPS Vehicle Routing Competition at NeurIPS 2022. Our methodology ranked first in this competition, outperforming all other approaches in solving the proposed dynamic vehicle routing problem. With this work, we provide a comprehensive numerical study that further highlights the efficacy and benefits of the proposed pipeline beyond the results achieved in the competition, e.g., by showcasing the robustness of the encoded policy against unseen instances and scenarios.

Learning-based Online Optimization for Autonomous Mobility-on-Demand Fleet Control

Autonomous mobility-on-demand systems are a viable alternative to mitigate many transportation-related externalities in cities, such as rising vehicle volumes in urban areas and transportation-related pollution. However, the success of these systems heavily depends on efficient and effective fleet control strategies. In this context, we study online control algorithms for autonomous mobility-on-demand systems and develop a novel hybrid combinatorial optimization enriched machine learning pipeline which learns online dispatching and rebalancing policies from optimal full-information solutions. We test our hybrid pipeline on large-scale real-world scenarios with different vehicle fleet sizes and various request densities. We show that our approach outperforms state-of-the-art greedy, and model-predictive control approaches with respect to various KPIs, e.g., by up to 17.1% and on average by 6.3% in terms of realized profit.