FastPart: Over-Parameterized Stochastic Gradient Descent for Sparse optimisation on Measures

This paper presents a novel algorithm that leverages Stochastic Gradient Descent strategies in conjunction with Random Features to augment the scalability of Conic Particle Gradient Descent (CPGD) specifically tailored for solving sparse optimisation problems on measures. By formulating the CPGD steps within a variational framework, we provide rigorous mathematical proofs demonstrating the following key findings: (i) The total variation norms of the solution measures along the descent trajectory remain bounded, ensuring stability and preventing undesirable divergence; (ii) We establish a global convergence guarantee with a convergence rate of $\mathcal{O}(\log(K)/\sqrt{K})$ over $K$ iterations, showcasing the efficiency and effectiveness of our algorithm; (iii) Additionally, we analyze and establish local control over the first-order condition discrepancy, contributing to a deeper understanding of the algorithm's behavior and reliability in practical applications.

Dual-sPLS: a family of Dual Sparse Partial Least Squares regressions for feature selection and prediction with tunable sparsity; evaluation on simulated and near-infrared data

Relating a set of variables X to a response y is crucial in chemometrics. A quantitative prediction objective can be enriched by qualitative data interpretation, for instance by locating the most influential features. When high-dimensional problems arise, dimension reduction techniques can be used. Most notable are projections (e.g. Partial Least Squares or PLS ) or variable selections (e.g. lasso). Sparse partial least squares combine both strategies, by blending variable selection into PLS. The variant presented in this paper, Dual-sPLS, generalizes the classical PLS1 algorithm. It provides balance between accurate prediction and efficient interpretation. It is based on penalizations inspired by classical regression methods (lasso, group lasso, least squares, ridge) and uses the dual norm notion. The resulting sparsity is enforced by an intuitive shrinking ratio parameter. Dual-sPLS favorably compares to similar regression methods, on simulated and real chemical data. Code is provided as an open-source package in R: \url{https://CRAN.R-project.org/package=dual.spls}.

Sparse Regularization for Mixture Problems

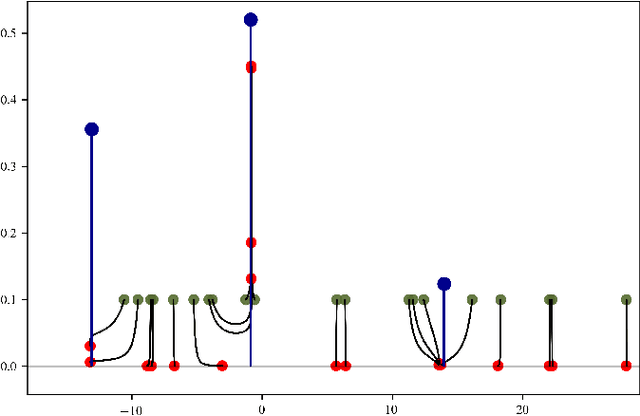
This paper investigates the statistical estimation of a discrete mixing measure $\mu^0$ involved in a kernel mixture model. Using some recent advances in $\ell_1$-regularization over the space of measures, we introduce a "data fitting + regularization" convex program for estimating $\mu^0$ in a grid-less manner, this method is referred to as Beurling-LASSO. Our contribution is two-fold: we derive a lower bound on the bandwidth of our data fitting term depending only on the support of $\mu^0$ and its so-called "minimum separation" to ensure quantitative support localization error bounds; and under a so-called "non-degenerate source condition" we derive a non-asymptotic support stability property. This latter shows that for sufficiently large sample size $n$, our estimator has exactly as many weighted Dirac masses as the target $\mu^0$, converging in amplitude and localization towards the true ones. The statistical performances of this estimator are investigated designing a so-called "dual certificate", which will be appropriate to our setting. Some classical situations, as e.g., Gaussian or ordinary smooth mixtures (e.g., Laplace distributions), are discussed at the end of the paper. We stress in particular that our method is completely adaptive w.r.t. the number of components involved in the mixture.

Classification with the nearest neighbor rule in general finite dimensional spaces: necessary and sufficient conditions

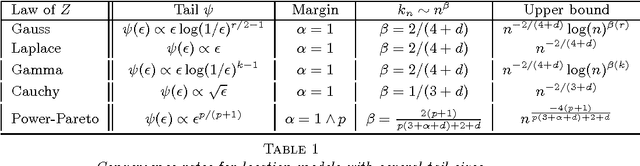
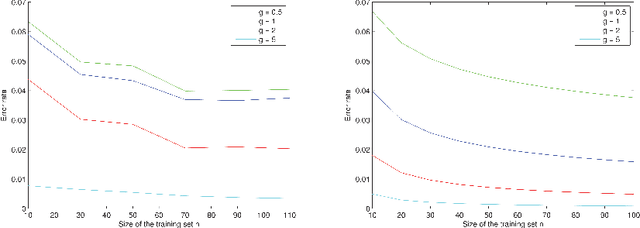
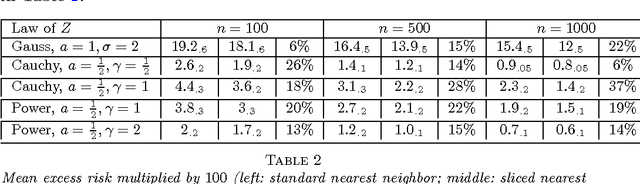
Given an $n$-sample of random vectors $(X_i,Y_i)_{1 \leq i \leq n}$ whose joint law is unknown, the long-standing problem of supervised classification aims to \textit{optimally} predict the label $Y$ of a given a new observation $X$. In this context, the nearest neighbor rule is a popular flexible and intuitive method in non-parametric situations. Even if this algorithm is commonly used in the machine learning and statistics communities, less is known about its prediction ability in general finite dimensional spaces, especially when the support of the density of the observations is $\mathbb{R}^d$. This paper is devoted to the study of the statistical properties of the nearest neighbor rule in various situations. In particular, attention is paid to the marginal law of $X$, as well as the smoothness and margin properties of the \textit{regression function} $\eta(X) = \mathbb{E}[Y | X]$. We identify two necessary and sufficient conditions to obtain uniform consistency rates of classification and to derive sharp estimates in the case of the nearest neighbor rule. Some numerical experiments are proposed at the end of the paper to help illustrate the discussion.