Gaussian Mixture Model with unknown diagonal covariances via continuous sparse regularization

This paper addresses the statistical estimation of Gaussian Mixture Models (GMMs) with unknown diagonal covariances from independent and identically distributed samples. We employ the Beurling-LASSO (BLASSO), a convex optimization framework that promotes sparsity in the space of measures, to simultaneously estimate the number of components and their parameters. Our main contribution extends the BLASSO methodology to multivariate GMMs with component-specific unknown diagonal covariance matrices-a significantly more flexible setting than previous approaches requiring known and identical covariances. We establish non-asymptotic recovery guarantees with nearly parametric convergence rates for component means, diagonal covariances, and weights, as well as for density prediction. A key theoretical contribution is the identification of an explicit separation condition on mixture components that enables the construction of non-degenerate dual certificates-essential tools for establishing statistical guarantees for the BLASSO. Our analysis leverages the Fisher-Rao geometry of the statistical model and introduces a novel semi-distance adapted to our framework, providing new insights into the interplay between component separation, parameter space geometry, and achievable statistical recovery.

Neural Networks beyond explainability: Selective inference for sequence motifs

Over the past decade, neural networks have been successful at making predictions from biological sequences, especially in the context of regulatory genomics. As in other fields of deep learning, tools have been devised to extract features such as sequence motifs that can explain the predictions made by a trained network. Here we intend to go beyond explainable machine learning and introduce SEISM, a selective inference procedure to test the association between these extracted features and the predicted phenotype. In particular, we discuss how training a one-layer convolutional network is formally equivalent to selecting motifs maximizing some association score. We adapt existing sampling-based selective inference procedures by quantizing this selection over an infinite set to a large but finite grid. Finally, we show that sampling under a specific choice of parameters is sufficient to characterize the composite null hypothesis typically used for selective inference-a result that goes well beyond our particular framework. We illustrate the behavior of our method in terms of calibration, power and speed and discuss its power/speed trade-off with a simpler data-split strategy. SEISM paves the way to an easier analysis of neural networks used in regulatory genomics, and to more powerful methods for genome wide association studies (GWAS).

Minimax Estimation of Partially-Observed Vector AutoRegressions

To understand the behavior of large dynamical systems like transportation networks, one must often rely on measurements transmitted by a set of sensors, for instance individual vehicles. Such measurements are likely to be incomplete and imprecise, which makes it hard to recover the underlying signal of interest.Hoping to quantify this phenomenon, we study the properties of a partially-observed state-space model. In our setting, the latent state $X$ follows a high-dimensional Vector AutoRegressive process $X_t = \theta X_{t-1} + \varepsilon_t$. Meanwhile, the observations $Y$ are given by a noise-corrupted random sample from the state $Y_t = \Pi_t X_t + \eta_t$. Several random sampling mechanisms are studied, allowing us to investigate the effect of spatial and temporal correlations in the distribution of the sampling matrices $\Pi_t$.We first prove a lower bound on the minimax estimation error for the transition matrix $\theta$. We then describe a sparse estimator based on the Dantzig selector and upper bound its non-asymptotic error, showing that it achieves the optimal convergence rate for most of our sampling mechanisms. Numerical experiments on simulated time series validate our theoretical findings, while an application to open railway data highlights the relevance of this model for public transport traffic analysis.

Towards off-the-grid algorithms for total variation regularized inverse problems

We introduce an algorithm to solve linear inverse problems regularized with the total (gradient) variation in a gridless manner. Contrary to most existing methods, that produce an approximate solution which is piecewise constant on a fixed mesh, our approach exploits the structure of the solutions and consists in iteratively constructing a linear combination of indicator functions of simple polygons.

Forecasting Nonnegative Time Series via Sliding Mask Method (SMM) and Latent Clustered Forecast (LCF)

We consider nonnegative time series forecasting framework. Based on recent advances in Nonnegative Matrix Factorization (NMF) and Archetypal Analysis, we introduce two procedures referred to as Sliding Mask Method (SMM) and Latent Clustered Forecast (LCF). SMM is a simple and powerful method based on time window prediction using Completion of Nonnegative Matrices. This new procedure combines low nonnegative rank decomposition and matrix completion where the hidden values are to be forecasted. LCF is two stage: it leverages archetypal analysis for dimension reduction and clustering of time series, then it uses any black-box supervised forecast solver on the clustered latent representation. Theoretical guarantees on uniqueness and robustness of the solution of NMF Completion-type problems are also provided for the first time. Finally, numerical experiments on real-world and synthetic data-set confirms forecasting accuracy for both the methodologies.

Concentration inequality for U-statistics of order two for uniformly ergodic Markov chains, and applications

We prove a new concentration inequality for U-statistics of order two for uniformly ergodic Markov chains. Working with bounded $\pi$-canonical kernels, we show that we can recover the convergence rate of Arcones and Gine (1993) who proved a concentration result for U-statistics of independent random variables and canonical kernels. Our proof relies on an inductive analysis where we use martingale techniques, uniform ergodicity, Nummelin splitting and Bernstein's type inequality where the spectral gap of the chain emerges. Our result allows us to conduct three applications. First, we establish a new exponential inequality for the estimation of spectra of trace class integral operators with MCMC methods. The novelty is that this result holds for kernels with positive and negative eigenvalues, which is new as far as we know. In addition, we investigate generalization performance of online algorithms working with pairwise loss functions and Markov chain samples. We provide an online-to-batch conversion result by showing how we can extract a low risk hypothesis from the sequence of hypotheses generated by any online learner. We finally give a non-asymptotic analysis of a goodness-of-fit test on the density of the invariant measure of a Markov chain. We identify the classes of alternatives over which our test based on the L2 distance has a prescribed power.

Markov Random Geometric Graph : A Growth Model for Temporal Dynamic Networks

We introduce Markov Random Geometric Graphs (MRGGs), a growth model for temporal dynamic networks. It is based on a Markovian latent space dynamic: consecutive latent points are sampled on the Euclidean Sphere using an unknown Markov kernel; and two nodes are connected with a probability depending on a unknown function of their latent geodesic distance. More precisely, at each stamp-time k we add a latent point X k sampled by jumping from the previous one X k--1 in a direction chosen uniformly Y k and with a length r k drawn from an unknown distribution called the latitude function. The connection probabilities between each pair of nodes are equal to the envelope function of the distance between these two latent points. We provide theoretical guarantees for the non-parametric estimation of the latitude and the envelope functions. We propose an efficient algorithm that achieves those non-parametric estimation tasks based on an ad-hoc Hierarchical Agglomerative Clustering approach, and we deploy this analysis on a real data-set given by exchange of messages on a social network.

Sparse Regularization for Mixture Problems

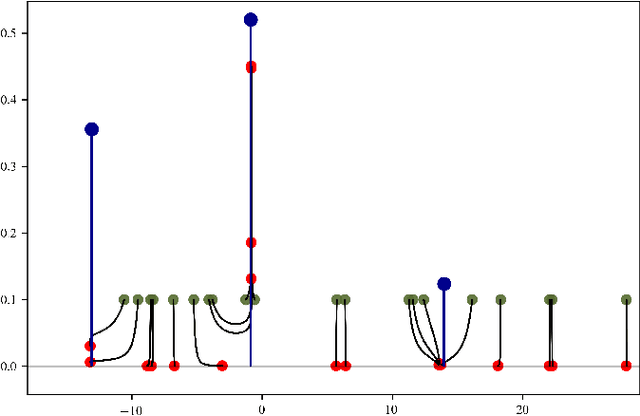
This paper investigates the statistical estimation of a discrete mixing measure $\mu^0$ involved in a kernel mixture model. Using some recent advances in $\ell_1$-regularization over the space of measures, we introduce a "data fitting + regularization" convex program for estimating $\mu^0$ in a grid-less manner, this method is referred to as Beurling-LASSO. Our contribution is two-fold: we derive a lower bound on the bandwidth of our data fitting term depending only on the support of $\mu^0$ and its so-called "minimum separation" to ensure quantitative support localization error bounds; and under a so-called "non-degenerate source condition" we derive a non-asymptotic support stability property. This latter shows that for sufficiently large sample size $n$, our estimator has exactly as many weighted Dirac masses as the target $\mu^0$, converging in amplitude and localization towards the true ones. The statistical performances of this estimator are investigated designing a so-called "dual certificate", which will be appropriate to our setting. Some classical situations, as e.g., Gaussian or ordinary smooth mixtures (e.g., Laplace distributions), are discussed at the end of the paper. We stress in particular that our method is completely adaptive w.r.t. the number of components involved in the mixture.

Optimal designs for Lasso and Dantzig selector using Expander Codes

We investigate the high-dimensional regression problem using adjacency matrices of unbalanced expander graphs. In this frame, we prove that the $\ell_{2}$-prediction error and the $\ell_{1}$-risk of the lasso and the Dantzig selector are optimal up to an explicit multiplicative constant. Thus we can estimate a high-dimensional target vector with an error term similar to the one obtained in a situation where one knows the support of the largest coordinates in advance. Moreover, we show that these design matrices have an explicit restricted eigenvalue. Precisely, they satisfy the restricted eigenvalue assumption and the compatibility condition with an explicit constant. Eventually, we capitalize on the recent construction of unbalanced expander graphs due to Guruswami, Umans, and Vadhan, to provide a deterministic polynomial time construction of these design matrices.