Cramér-Rao bound-informed training of neural networks for quantitative MRI

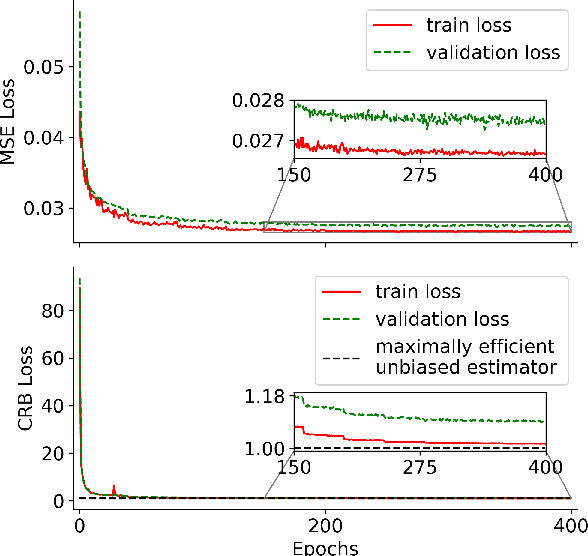
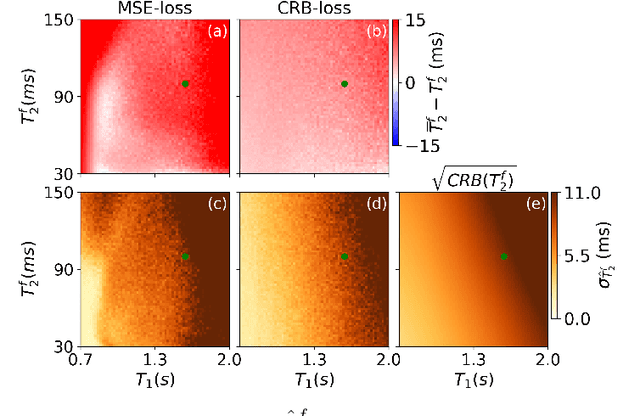
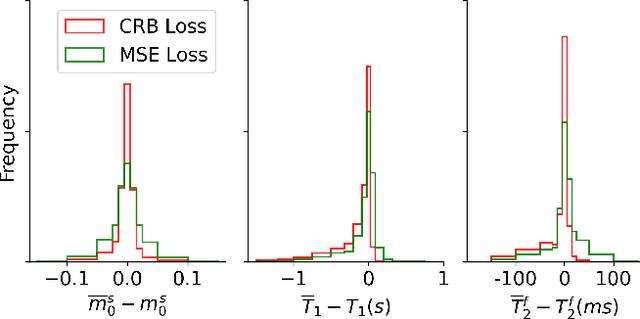
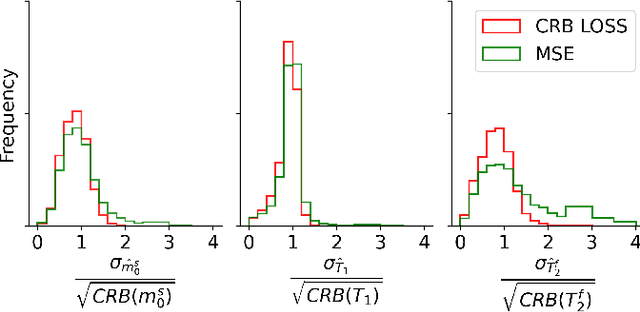
Neural networks are increasingly used to estimate parameters in quantitative MRI, in particular in magnetic resonance fingerprinting. Their advantages over the gold standard non-linear least square fitting are their superior speed and their immunity to the non-convexity of many fitting problems. We find, however, that in heterogeneous parameter spaces, i.e. in spaces in which the variance of the estimated parameters varies considerably, good performance is hard to achieve and requires arduous tweaking of the loss function, hyper parameters, and the distribution of the training data in parameter space. Here, we address these issues with a theoretically well-founded loss function: the Cram\'er-Rao bound (CRB) provides a theoretical lower bound for the variance of an unbiased estimator and we propose to normalize the squared error with respective CRB. With this normalization, we balance the contributions of hard-to-estimate and not-so-hard-to-estimate parameters and areas in parameter space, and avoid a dominance of the former in the overall training loss. Further, the CRB-based loss function equals one for a maximally-efficient unbiased estimator, which we consider the ideal estimator. Hence, the proposed CRB-based loss function provides an absolute evaluation metric. We compare a network trained with the CRB-based loss with a network trained with the commonly used means squared error loss and demonstrate the advantages of the former in numerical, phantom, and in vivo experiments.

Three rates of convergence or separation via U-statistics in a dependent framework

Despite the ubiquity of U-statistics in modern Probability and Statistics, their non-asymptotic analysis in a dependent framework may have been overlooked. In a recent work, a new concentration inequality for U-statistics of order two for uniformly ergodic Markov chains has been proved. In this paper, we put this theoretical breakthrough into action by pushing further the current state of knowledge in three different active fields of research. First, we establish a new exponential inequality for the estimation of spectra of trace class integral operators with MCMC methods. The novelty is that this result holds for kernels with positive and negative eigenvalues, which is new as far as we know. In addition, we investigate generalization performance of online algorithms working with pairwise loss functions and Markov chain samples. We provide an online-to-batch conversion result by showing how we can extract a low risk hypothesis from the sequence of hypotheses generated by any online learner. We finally give a non-asymptotic analysis of a goodness-of-fit test on the density of the invariant measure of a Markov chain. We identify some classes of alternatives over which our test based on the $L_2$ distance has a prescribed power.

Concentration inequality for U-statistics of order two for uniformly ergodic Markov chains, and applications

We prove a new concentration inequality for U-statistics of order two for uniformly ergodic Markov chains. Working with bounded $\pi$-canonical kernels, we show that we can recover the convergence rate of Arcones and Gine (1993) who proved a concentration result for U-statistics of independent random variables and canonical kernels. Our proof relies on an inductive analysis where we use martingale techniques, uniform ergodicity, Nummelin splitting and Bernstein's type inequality where the spectral gap of the chain emerges. Our result allows us to conduct three applications. First, we establish a new exponential inequality for the estimation of spectra of trace class integral operators with MCMC methods. The novelty is that this result holds for kernels with positive and negative eigenvalues, which is new as far as we know. In addition, we investigate generalization performance of online algorithms working with pairwise loss functions and Markov chain samples. We provide an online-to-batch conversion result by showing how we can extract a low risk hypothesis from the sequence of hypotheses generated by any online learner. We finally give a non-asymptotic analysis of a goodness-of-fit test on the density of the invariant measure of a Markov chain. We identify the classes of alternatives over which our test based on the L2 distance has a prescribed power.

Markov Random Geometric Graph : A Growth Model for Temporal Dynamic Networks

We introduce Markov Random Geometric Graphs (MRGGs), a growth model for temporal dynamic networks. It is based on a Markovian latent space dynamic: consecutive latent points are sampled on the Euclidean Sphere using an unknown Markov kernel; and two nodes are connected with a probability depending on a unknown function of their latent geodesic distance. More precisely, at each stamp-time k we add a latent point X k sampled by jumping from the previous one X k--1 in a direction chosen uniformly Y k and with a length r k drawn from an unknown distribution called the latitude function. The connection probabilities between each pair of nodes are equal to the envelope function of the distance between these two latent points. We provide theoretical guarantees for the non-parametric estimation of the latitude and the envelope functions. We propose an efficient algorithm that achieves those non-parametric estimation tasks based on an ad-hoc Hierarchical Agglomerative Clustering approach, and we deploy this analysis on a real data-set given by exchange of messages on a social network.

Inference in the Stochastic Block Model with a Markovian assignment of the communities

We tackle the community detection problem in the Stochastic Block Model (SBM) when the communities of the nodes of the graph are assigned with a Markovian dynamic. To recover the partition of the nodes, we adapt the relaxed K-means SDP program presented in [11]. We identify the relevant signal-to-noise ratio (SNR) in our framework and we prove that the misclassification error decays exponentially fast with respect to this SNR. We provide infinity norm consistent estimation of the parameters of our model and we discuss our results through the prism of classical degree regimes of the SBMs' literature. MSC 2010 subject classifications: Primary 68Q32; secondary 68R10, 90C35.