Performance evaluation of Reddit Comments using Machine Learning and Natural Language Processing methods in Sentiment Analysis

Sentiment analysis, an increasingly vital field in both academia and industry, plays a pivotal role in machine learning applications, particularly on social media platforms like Reddit. However, the efficacy of sentiment analysis models is hindered by the lack of expansive and fine-grained emotion datasets. To address this gap, our study leverages the GoEmotions dataset, comprising a diverse range of emotions, to evaluate sentiment analysis methods across a substantial corpus of 58,000 comments. Distinguished from prior studies by the Google team, which limited their analysis to only two models, our research expands the scope by evaluating a diverse array of models. We investigate the performance of traditional classifiers such as Naive Bayes and Support Vector Machines (SVM), as well as state-of-the-art transformer-based models including BERT, RoBERTa, and GPT. Furthermore, our evaluation criteria extend beyond accuracy to encompass nuanced assessments, including hierarchical classification based on varying levels of granularity in emotion categorization. Additionally, considerations such as computational efficiency are incorporated to provide a comprehensive evaluation framework. Our findings reveal that the RoBERTa model consistently outperforms the baseline models, demonstrating superior accuracy in fine-grained sentiment classification tasks. This underscores the substantial potential and significance of the RoBERTa model in advancing sentiment analysis capabilities.

Advanced Conditional Variational Autoencoders (A-CVAE): Towards interpreting open-domain conversation generation via disentangling latent feature representation

Currently end-to-end deep learning based open-domain dialogue systems remain black box models, making it easy to generate irrelevant contents with data-driven models. Specifically, latent variables are highly entangled with different semantics in the latent space due to the lack of priori knowledge to guide the training. To address this problem, this paper proposes to harness the generative model with a priori knowledge through a cognitive approach involving mesoscopic scale feature disentanglement. Particularly, the model integrates the macro-level guided-category knowledge and micro-level open-domain dialogue data for the training, leveraging the priori knowledge into the latent space, which enables the model to disentangle the latent variables within the mesoscopic scale. Besides, we propose a new metric for open-domain dialogues, which can objectively evaluate the interpretability of the latent space distribution. Finally, we validate our model on different datasets and experimentally demonstrate that our model is able to generate higher quality and more interpretable dialogues than other models.

Cramér-Rao bound-informed training of neural networks for quantitative MRI

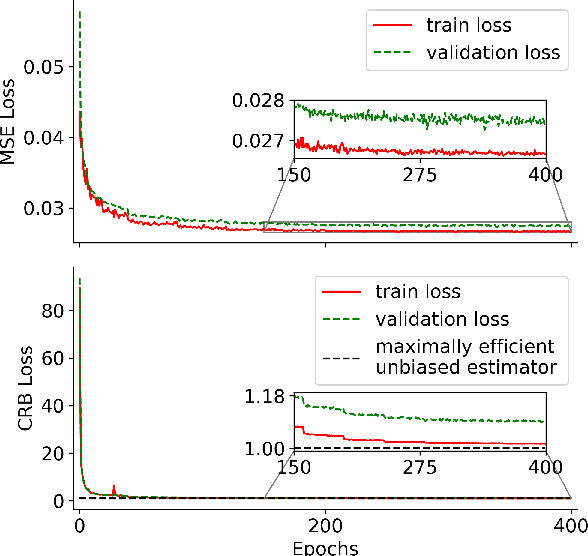
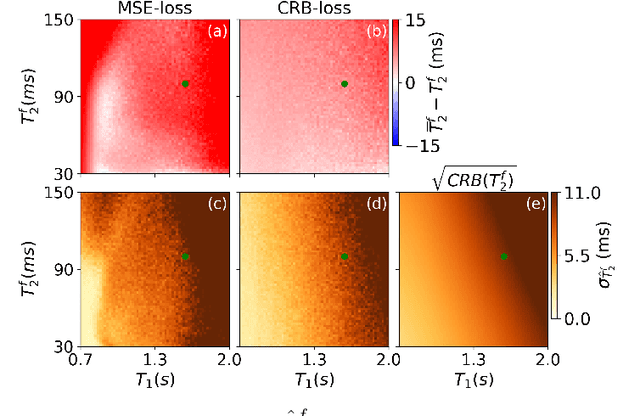
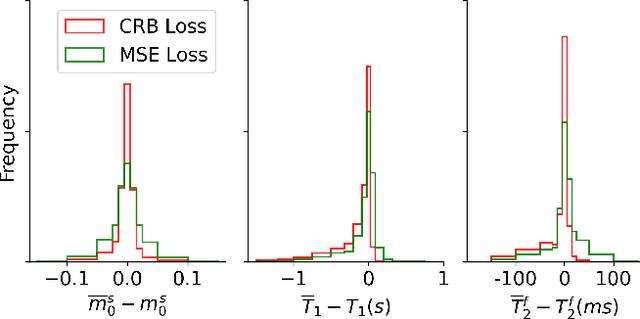
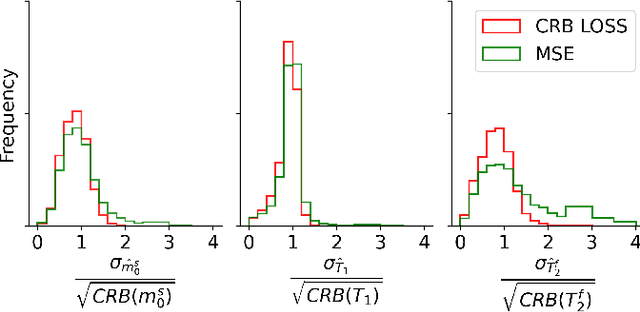
Neural networks are increasingly used to estimate parameters in quantitative MRI, in particular in magnetic resonance fingerprinting. Their advantages over the gold standard non-linear least square fitting are their superior speed and their immunity to the non-convexity of many fitting problems. We find, however, that in heterogeneous parameter spaces, i.e. in spaces in which the variance of the estimated parameters varies considerably, good performance is hard to achieve and requires arduous tweaking of the loss function, hyper parameters, and the distribution of the training data in parameter space. Here, we address these issues with a theoretically well-founded loss function: the Cram\'er-Rao bound (CRB) provides a theoretical lower bound for the variance of an unbiased estimator and we propose to normalize the squared error with respective CRB. With this normalization, we balance the contributions of hard-to-estimate and not-so-hard-to-estimate parameters and areas in parameter space, and avoid a dominance of the former in the overall training loss. Further, the CRB-based loss function equals one for a maximally-efficient unbiased estimator, which we consider the ideal estimator. Hence, the proposed CRB-based loss function provides an absolute evaluation metric. We compare a network trained with the CRB-based loss with a network trained with the commonly used means squared error loss and demonstrate the advantages of the former in numerical, phantom, and in vivo experiments.