Contrast-Optimized Basis Functions for Self-Navigated Motion Correction in Quantitative MRI

Purpose: The long scan times of quantitative MRI techniques make motion artifacts more likely. For MR-Fingerprinting-like approaches, this problem can be addressed with self-navigated retrospective motion correction based on reconstructions in a singular value decomposition (SVD) subspace. However, the SVD promotes high signal intensity in all tissues, which limits the contrast between tissue types and ultimately reduces the accuracy of registration. The purpose of this paper is to rotate the subspace for maximum contrast between two types of tissue and improve the accuracy of motion estimates. Methods: A subspace is derived that promotes contrasts between brain parenchyma and CSF, achieved through the generalized eigendecomposition of mean autocorrelation matrices, followed by a Gram-Schmidt process to maintain orthogonality. We tested our motion correction method on 85 scans with varying motion levels, acquired with a 3D hybrid-state sequence optimized for quantitative magnetization transfer imaging. Results: A comparative analysis shows that the contrast-optimized basis significantly improve the parenchyma-CSF contrast, leading to smoother motion estimates and reduced artifacts in the quantitative maps. Conclusion: The proposed contrast-optimized subspace improves the accuracy of the motion estimation.

Cramér-Rao bound-informed training of neural networks for quantitative MRI

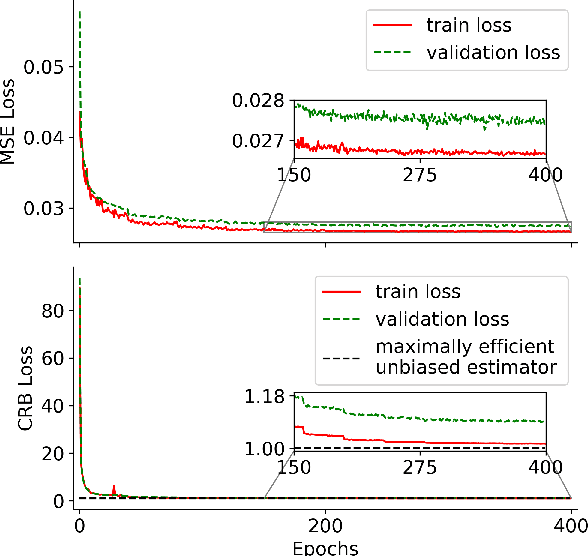
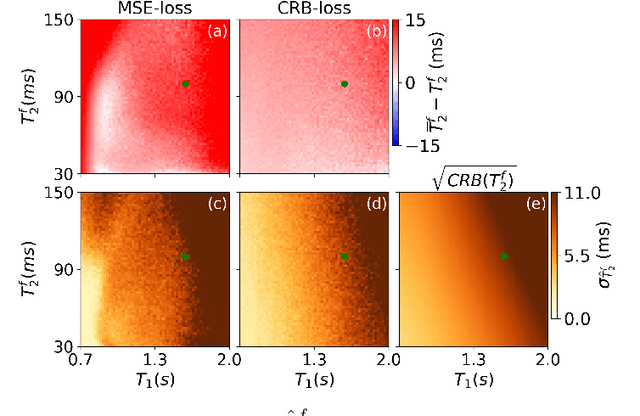
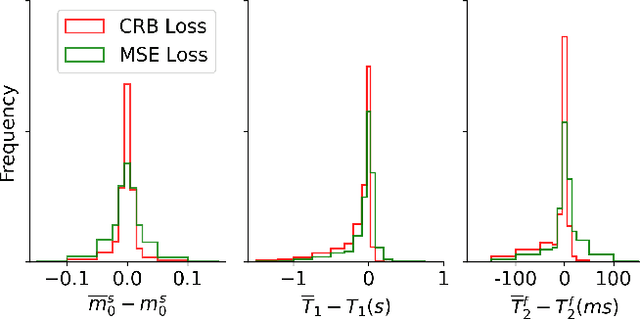
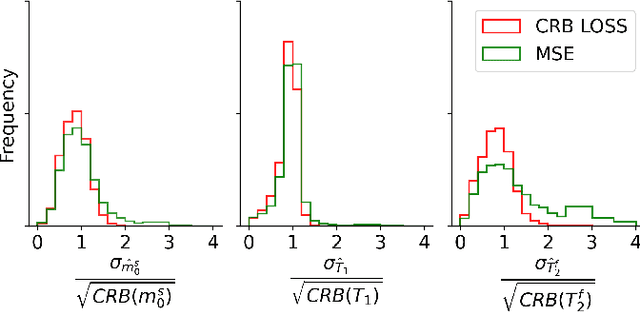
Neural networks are increasingly used to estimate parameters in quantitative MRI, in particular in magnetic resonance fingerprinting. Their advantages over the gold standard non-linear least square fitting are their superior speed and their immunity to the non-convexity of many fitting problems. We find, however, that in heterogeneous parameter spaces, i.e. in spaces in which the variance of the estimated parameters varies considerably, good performance is hard to achieve and requires arduous tweaking of the loss function, hyper parameters, and the distribution of the training data in parameter space. Here, we address these issues with a theoretically well-founded loss function: the Cram\'er-Rao bound (CRB) provides a theoretical lower bound for the variance of an unbiased estimator and we propose to normalize the squared error with respective CRB. With this normalization, we balance the contributions of hard-to-estimate and not-so-hard-to-estimate parameters and areas in parameter space, and avoid a dominance of the former in the overall training loss. Further, the CRB-based loss function equals one for a maximally-efficient unbiased estimator, which we consider the ideal estimator. Hence, the proposed CRB-based loss function provides an absolute evaluation metric. We compare a network trained with the CRB-based loss with a network trained with the commonly used means squared error loss and demonstrate the advantages of the former in numerical, phantom, and in vivo experiments.