FastPart: Over-Parameterized Stochastic Gradient Descent for Sparse optimisation on Measures

This paper presents a novel algorithm that leverages Stochastic Gradient Descent strategies in conjunction with Random Features to augment the scalability of Conic Particle Gradient Descent (CPGD) specifically tailored for solving sparse optimisation problems on measures. By formulating the CPGD steps within a variational framework, we provide rigorous mathematical proofs demonstrating the following key findings: (i) The total variation norms of the solution measures along the descent trajectory remain bounded, ensuring stability and preventing undesirable divergence; (ii) We establish a global convergence guarantee with a convergence rate of $\mathcal{O}(\log(K)/\sqrt{K})$ over $K$ iterations, showcasing the efficiency and effectiveness of our algorithm; (iii) Additionally, we analyze and establish local control over the first-order condition discrepancy, contributing to a deeper understanding of the algorithm's behavior and reliability in practical applications.

Stochastic Langevin Monte Carlo for (weakly) log-concave posterior distributions

In this paper, we investigate a continuous time version of the Stochastic Langevin Monte Carlo method, introduced in [WT11], that incorporates a stochastic sampling step inside the traditional over-damped Langevin diffusion. This method is popular in machine learning for sampling posterior distribution. We will pay specific attention in our work to the computational cost in terms of $n$ (the number of observations that produces the posterior distribution), and $d$ (the dimension of the ambient space where the parameter of interest is living). We derive our analysis in the weakly convex framework, which is parameterized with the help of the Kurdyka-\L ojasiewicz (KL) inequality, that permits to handle a vanishing curvature settings, which is far less restrictive when compared to the simple strongly convex case. We establish that the final horizon of simulation to obtain an $\varepsilon$ approximation (in terms of entropy) is of the order $( d \log(n)^2 )^{(1+r)^2} [\log^2(\varepsilon^{-1}) + n^2 d^{2(1+r)} \log^{4(1+r)}(n) ]$ with a Poissonian subsampling of parameter $\left(n ( d \log^2(n))^{1+r}\right)^{-1}$, where the parameter $r$ is involved in the KL inequality and varies between $0$ (strongly convex case) and $1$ (limiting Laplace situation).

Asymptotic study of stochastic adaptive algorithm in non-convex landscape

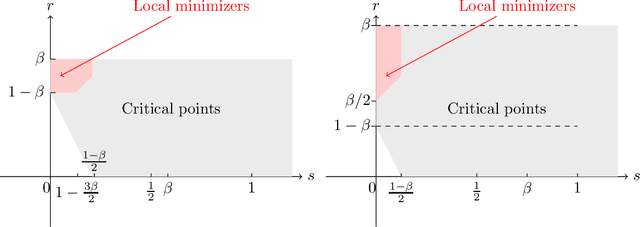
This paper studies some asymptotic properties of adaptive algorithms widely used in optimization and machine learning, and among them Adagrad and Rmsprop, which are involved in most of the blackbox deep learning algorithms. Our setup is the non-convex landscape optimization point of view, we consider a one time scale parametrization and we consider the situation where these algorithms may be used or not with mini-batches. We adopt the point of view of stochastic algorithms and establish the almost sure convergence of these methods when using a decreasing step-size point of view towards the set of critical points of the target function. With a mild extra assumption on the noise, we also obtain the convergence towards the set of minimizer of the function. Along our study, we also obtain a "convergence rate" of the methods, in the vein of the works of \cite{GhadimiLan}.

On the cost of Bayesian posterior mean strategy for log-concave models

In this paper, we investigate the problem of computing Bayesian estimators using Langevin Monte-Carlo type approximation. The novelty of this paper is to consider together the statistical and numerical counterparts (in a general log-concave setting). More precisely, we address the following question: given $n$ observations in $\mathbb{R}^q$ distributed under an unknown probability $\mathbb{P}_{\theta^\star}$ with $\theta^\star \in \mathbb{R}^d$ , what is the optimal numerical strategy and its cost for the approximation of $\theta^\star$ with the Bayesian posterior mean? To answer this question, we establish some quantitative statistical bounds related to the underlying Poincar\'e constant of the model and establish new results about the numerical approximation of Gibbs measures by Cesaro averages of Euler schemes of (over-damped) Langevin diffusions. These last results include in particular some quantitative controls in the weakly convex case based on new bounds on the solution of the related Poisson equation of the diffusion.

Sparse Regularization for Mixture Problems

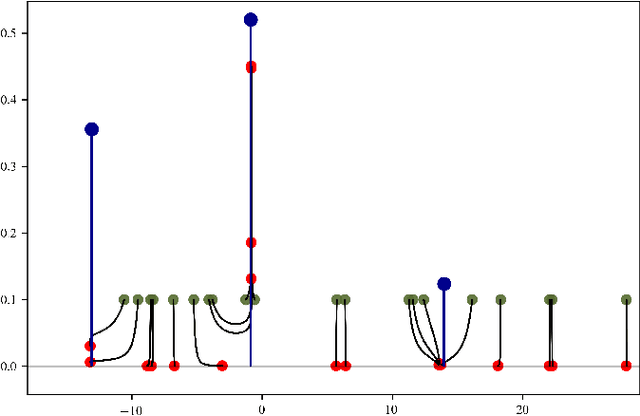
This paper investigates the statistical estimation of a discrete mixing measure $\mu^0$ involved in a kernel mixture model. Using some recent advances in $\ell_1$-regularization over the space of measures, we introduce a "data fitting + regularization" convex program for estimating $\mu^0$ in a grid-less manner, this method is referred to as Beurling-LASSO. Our contribution is two-fold: we derive a lower bound on the bandwidth of our data fitting term depending only on the support of $\mu^0$ and its so-called "minimum separation" to ensure quantitative support localization error bounds; and under a so-called "non-degenerate source condition" we derive a non-asymptotic support stability property. This latter shows that for sufficiently large sample size $n$, our estimator has exactly as many weighted Dirac masses as the target $\mu^0$, converging in amplitude and localization towards the true ones. The statistical performances of this estimator are investigated designing a so-called "dual certificate", which will be appropriate to our setting. Some classical situations, as e.g., Gaussian or ordinary smooth mixtures (e.g., Laplace distributions), are discussed at the end of the paper. We stress in particular that our method is completely adaptive w.r.t. the number of components involved in the mixture.

Stochastic Heavy Ball

This paper deals with a natural stochastic optimization procedure derived from the so-called Heavy-ball method differential equation, which was introduced by Polyak in the 1960s with his seminal contribution [Pol64]. The Heavy-ball method is a second-order dynamics that was investigated to minimize convex functions f . The family of second-order methods recently received a large amount of attention, until the famous contribution of Nesterov [Nes83], leading to the explosion of large-scale optimization problems. This work provides an in-depth description of the stochastic heavy-ball method, which is an adaptation of the deterministic one when only unbiased evalutions of the gradient are available and used throughout the iterations of the algorithm. We first describe some almost sure convergence results in the case of general non-convex coercive functions f . We then examine the situation of convex and strongly convex potentials and derive some non-asymptotic results about the stochastic heavy-ball method. We end our study with limit theorems on several rescaled algorithms.

Regret bounds for Narendra-Shapiro bandit algorithms

Narendra-Shapiro (NS) algorithms are bandit-type algorithms that have been introduced in the sixties (with a view to applications in Psychology or learning automata), whose convergence has been intensively studied in the stochastic algorithm literature. In this paper, we adress the following question: are the Narendra-Shapiro (NS) bandit algorithms competitive from a \textit{regret} point of view? In our main result, we show that some competitive bounds can be obtained for such algorithms in their penalized version (introduced in \cite{Lamberton_Pages}). More precisely, up to an over-penalization modification, the pseudo-regret $\bar{R}_n$ related to the penalized two-armed bandit algorithm is uniformly bounded by $C \sqrt{n}$ (where $C$ is made explicit in the paper). \noindent We also generalize existing convergence and rates of convergence results to the multi-armed case of the over-penalized bandit algorithm, including the convergence toward the invariant measure of a Piecewise Deterministic Markov Process (PDMP) after a suitable renormalization. Finally, ergodic properties of this PDMP are given in the multi-armed case.

Classification with the nearest neighbor rule in general finite dimensional spaces: necessary and sufficient conditions

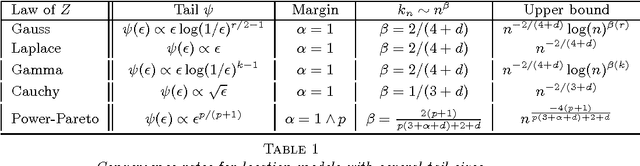
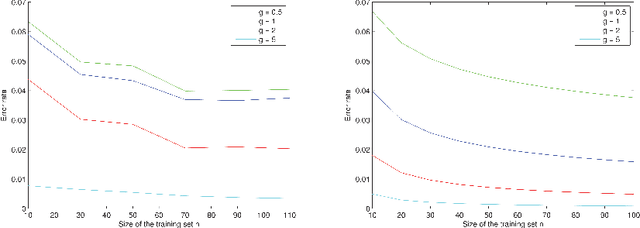
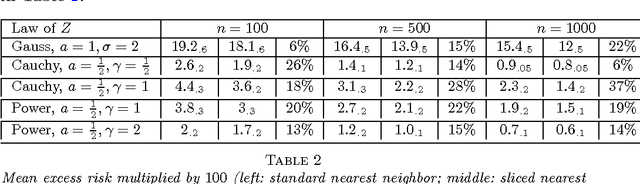
Given an $n$-sample of random vectors $(X_i,Y_i)_{1 \leq i \leq n}$ whose joint law is unknown, the long-standing problem of supervised classification aims to \textit{optimally} predict the label $Y$ of a given a new observation $X$. In this context, the nearest neighbor rule is a popular flexible and intuitive method in non-parametric situations. Even if this algorithm is commonly used in the machine learning and statistics communities, less is known about its prediction ability in general finite dimensional spaces, especially when the support of the density of the observations is $\mathbb{R}^d$. This paper is devoted to the study of the statistical properties of the nearest neighbor rule in various situations. In particular, attention is paid to the marginal law of $X$, as well as the smoothness and margin properties of the \textit{regression function} $\eta(X) = \mathbb{E}[Y | X]$. We identify two necessary and sufficient conditions to obtain uniform consistency rates of classification and to derive sharp estimates in the case of the nearest neighbor rule. Some numerical experiments are proposed at the end of the paper to help illustrate the discussion.