Asymptotic study of stochastic adaptive algorithm in non-convex landscape

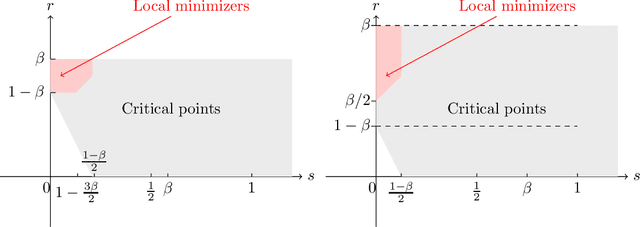
This paper studies some asymptotic properties of adaptive algorithms widely used in optimization and machine learning, and among them Adagrad and Rmsprop, which are involved in most of the blackbox deep learning algorithms. Our setup is the non-convex landscape optimization point of view, we consider a one time scale parametrization and we consider the situation where these algorithms may be used or not with mini-batches. We adopt the point of view of stochastic algorithms and establish the almost sure convergence of these methods when using a decreasing step-size point of view towards the set of critical points of the target function. With a mild extra assumption on the noise, we also obtain the convergence towards the set of minimizer of the function. Along our study, we also obtain a "convergence rate" of the methods, in the vein of the works of \cite{GhadimiLan}.

Convergence rate of a simulated annealing algorithm with noisy observations

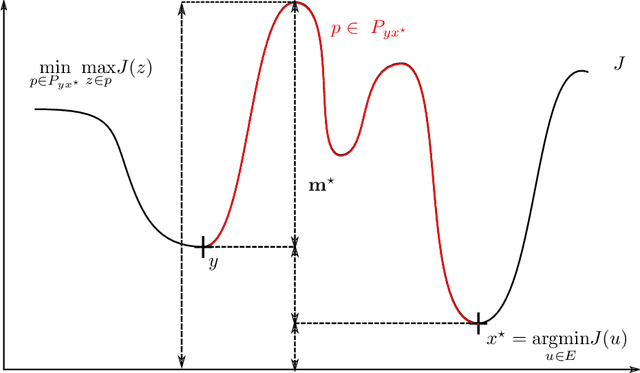
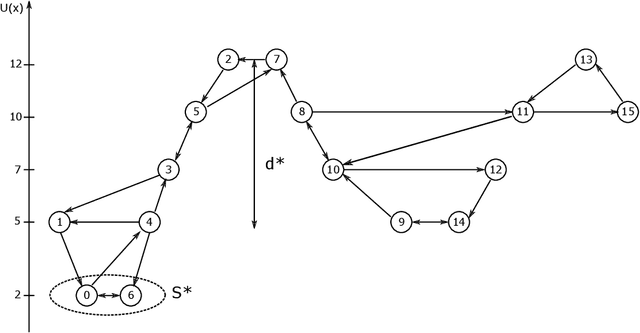
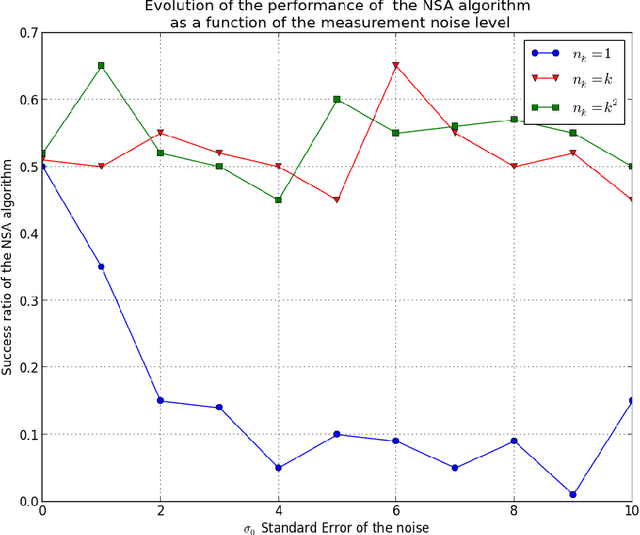
In this paper we propose a modified version of the simulated annealing algorithm for solving a stochastic global optimization problem. More precisely, we address the problem of finding a global minimizer of a function with noisy evaluations. We provide a rate of convergence and its optimized parametrization to ensure a minimal number of evaluations for a given accuracy and a confidence level close to 1. This work is completed with a set of numerical experimentations and assesses the practical performance both on benchmark test cases and on real world examples.