Regret analysis of the Piyavskii-Shubert algorithm for global Lipschitz optimization

We consider the problem of maximizing a non-concave Lipschitz multivariate function f over a compact domain. We provide regret guarantees (i.e., optimization error bounds) for a very natural algorithm originally designed by Piyavskii and Shubert in 1972. Our results hold in a general setting in which values of f can only be accessed approximately. In particular, they yield state-of-the-art regret bounds both when f is observed exactly and when evaluations are perturbed by an independent subgaussian noise.

Convergence rate of a simulated annealing algorithm with noisy observations

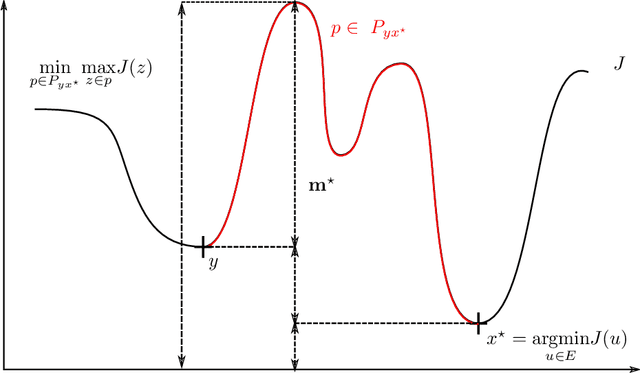
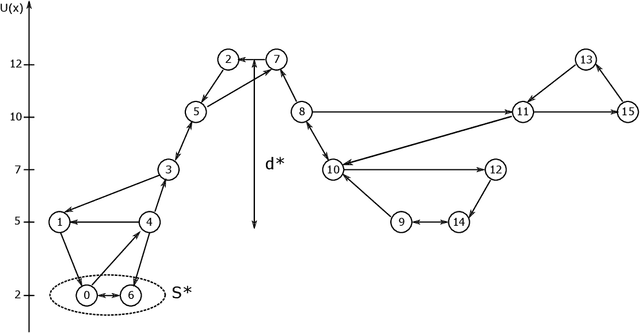
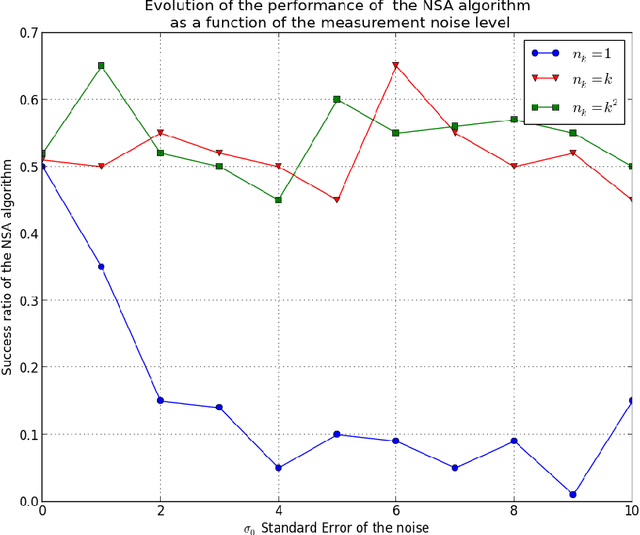
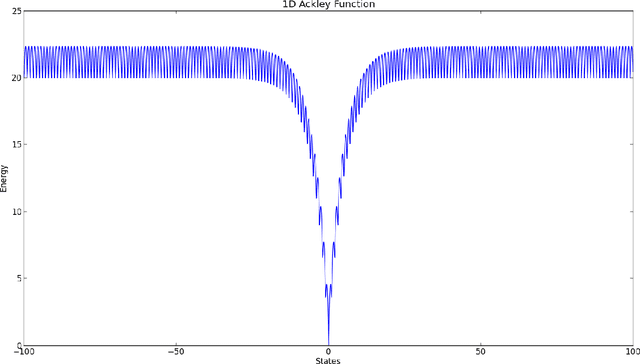
In this paper we propose a modified version of the simulated annealing algorithm for solving a stochastic global optimization problem. More precisely, we address the problem of finding a global minimizer of a function with noisy evaluations. We provide a rate of convergence and its optimized parametrization to ensure a minimal number of evaluations for a given accuracy and a confidence level close to 1. This work is completed with a set of numerical experimentations and assesses the practical performance both on benchmark test cases and on real world examples.