Regret analysis of the Piyavskii-Shubert algorithm for global Lipschitz optimization

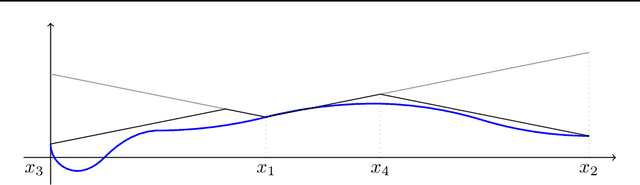
We consider the problem of maximizing a non-concave Lipschitz multivariate function f over a compact domain. We provide regret guarantees (i.e., optimization error bounds) for a very natural algorithm originally designed by Piyavskii and Shubert in 1972. Our results hold in a general setting in which values of f can only be accessed approximately. In particular, they yield state-of-the-art regret bounds both when f is observed exactly and when evaluations are perturbed by an independent subgaussian noise.