Efficient Robust Conformal Prediction via Lipschitz-Bounded Networks

Conformal Prediction (CP) has proven to be an effective post-hoc method for improving the trustworthiness of neural networks by providing prediction sets with finite-sample guarantees. However, under adversarial attacks, classical conformal guarantees do not hold anymore: this problem is addressed in the field of Robust Conformal Prediction. Several methods have been proposed to provide robust CP sets with guarantees under adversarial perturbations, but, for large scale problems, these sets are either too large or the methods are too computationally demanding to be deployed in real life scenarios. In this work, we propose a new method that leverages Lipschitz-bounded networks to precisely and efficiently estimate robust CP sets. When combined with a 1-Lipschitz robust network, we demonstrate that our lip-rcp method outperforms state-of-the-art results in both the size of the robust CP sets and computational efficiency in medium and large-scale scenarios such as ImageNet. Taking a different angle, we also study vanilla CP under attack, and derive new worst-case coverage bounds of vanilla CP sets, which are valid simultaneously for all adversarial attack levels. Our lip-rcp method makes this second approach as efficient as vanilla CP while also allowing robustness guarantees.

Conformal Object Detection by Sequential Risk Control

Recent advances in object detectors have led to their adoption for industrial uses. However, their deployment in critical applications is hindered by the inherent lack of reliability of neural networks and the complex structure of object detection models. To address these challenges, we turn to Conformal Prediction, a post-hoc procedure which offers statistical guarantees that are valid for any dataset size, without requiring prior knowledge on the model or data distribution. Our contribution is manifold: first, we formally define the problem of Conformal Object Detection (COD) and introduce a novel method, Sequential Conformal Risk Control (SeqCRC), that extends the statistical guarantees of Conformal Risk Control (CRC) to two sequential tasks with two parameters, as required in the COD setting. Then, we propose loss functions and prediction sets suited to applying CRC to different applications and certification requirements. Finally, we present a conformal toolkit, enabling replication and further exploration of our methods. Using this toolkit, we perform extensive experiments, yielding a benchmark that validates the investigated methods and emphasizes trade-offs and other practical consequences.

Adaptive approximation of monotone functions

We study the classical problem of approximating a non-decreasing function $f: \mathcal{X} \to \mathcal{Y}$ in $L^p(\mu)$ norm by sequentially querying its values, for known compact real intervals $\mathcal{X}$, $\mathcal{Y}$ and a known probability measure $\mu$ on $\cX$. For any function~$f$ we characterize the minimum number of evaluations of $f$ that algorithms need to guarantee an approximation $\hat{f}$ with an $L^p(\mu)$ error below $\epsilon$ after stopping. Unlike worst-case results that hold uniformly over all $f$, our complexity measure is dependent on each specific function $f$. To address this problem, we introduce GreedyBox, a generalization of an algorithm originally proposed by Novak (1992) for numerical integration. We prove that GreedyBox achieves an optimal sample complexity for any function $f$, up to logarithmic factors. Additionally, we uncover results regarding piecewise-smooth functions. Perhaps as expected, the $L^p(\mu)$ error of GreedyBox decreases much faster for piecewise-$C^2$ functions than predicted by the algorithm (without any knowledge on the smoothness of $f$). A simple modification even achieves optimal minimax approximation rates for such functions, which we compute explicitly. In particular, our findings highlight multiple performance gaps between adaptive and non-adaptive algorithms, smooth and piecewise-smooth functions, as well as monotone or non-monotone functions. Finally, we provide numerical experiments to support our theoretical results.

Certified Multi-Fidelity Zeroth-Order Optimization

We consider the problem of multi-fidelity zeroth-order optimization, where one can evaluate a function $f$ at various approximation levels (of varying costs), and the goal is to optimize $f$ with the cheapest evaluations possible. In this paper, we study \emph{certified} algorithms, which are additionally required to output a data-driven upper bound on the optimization error. We first formalize the problem in terms of a min-max game between an algorithm and an evaluation environment. We then propose a certified variant of the MFDOO algorithm and derive a bound on its cost complexity for any Lipschitz function $f$. We also prove an $f$-dependent lower bound showing that this algorithm has a near-optimal cost complexity. We close the paper by addressing the special case of noisy (stochastic) evaluations as a direct example.

A general approximation lower bound in $L^p$ norm, with applications to feed-forward neural networks

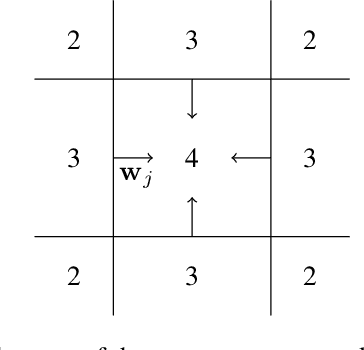
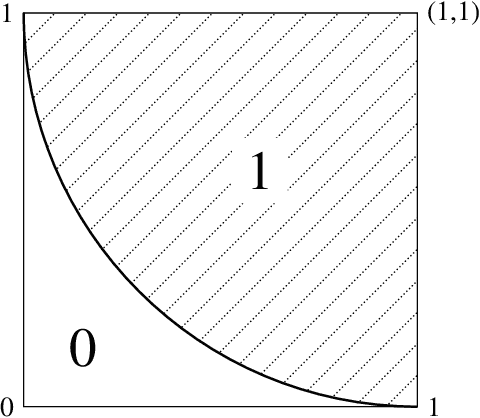
We study the fundamental limits to the expressive power of neural networks. Given two sets $F$, $G$ of real-valued functions, we first prove a general lower bound on how well functions in $F$ can be approximated in $L^p(\mu)$ norm by functions in $G$, for any $p \geq 1$ and any probability measure $\mu$. The lower bound depends on the packing number of $F$, the range of $F$, and the fat-shattering dimension of $G$. We then instantiate this bound to the case where $G$ corresponds to a piecewise-polynomial feed-forward neural network, and describe in details the application to two sets $F$: H{\"o}lder balls and multivariate monotonic functions. Beside matching (known or new) upper bounds up to log factors, our lower bounds shed some light on the similarities or differences between approximation in $L^p$ norm or in sup norm, solving an open question by DeVore et al. (2021). Our proof strategy differs from the sup norm case and uses a key probability result of Mendelson (2002).

Numerical influence of ReLU'(0) on backpropagation

In theory, the choice of ReLU'(0) in [0, 1] for a neural network has a negligible influence both on backpropagation and training. Yet, in the real world, 32 bits default precision combined with the size of deep learning problems makes it a hyperparameter of training methods. We investigate the importance of the value of ReLU'(0) for several precision levels (16, 32, 64 bits), on various networks (fully connected, VGG, ResNet) and datasets (MNIST, CIFAR10, SVHN). We observe considerable variations of backpropagation outputs which occur around half of the time in 32 bits precision. The effect disappears with double precision, while it is systematic at 16 bits. For vanilla SGD training, the choice ReLU'(0) = 0 seems to be the most efficient. We also evidence that reconditioning approaches as batch-norm or ADAM tend to buffer the influence of ReLU'(0)'s value. Overall, the message we want to convey is that algorithmic differentiation of nonsmooth problems potentially hides parameters that could be tuned advantageously.

White Paper Machine Learning in Certified Systems

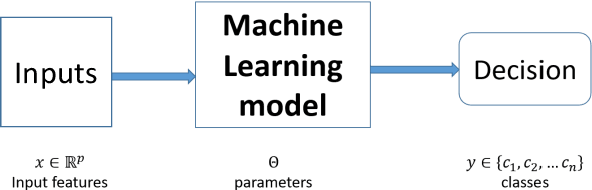
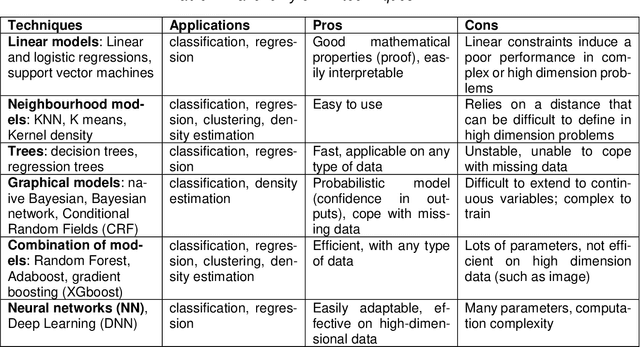
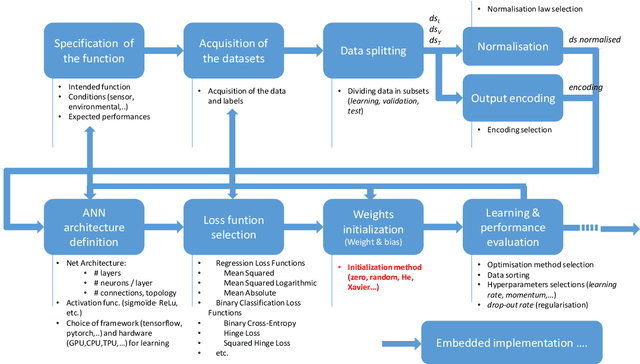
Machine Learning (ML) seems to be one of the most promising solution to automate partially or completely some of the complex tasks currently realized by humans, such as driving vehicles, recognizing voice, etc. It is also an opportunity to implement and embed new capabilities out of the reach of classical implementation techniques. However, ML techniques introduce new potential risks. Therefore, they have only been applied in systems where their benefits are considered worth the increase of risk. In practice, ML techniques raise multiple challenges that could prevent their use in systems submitted to certification constraints. But what are the actual challenges? Can they be overcome by selecting appropriate ML techniques, or by adopting new engineering or certification practices? These are some of the questions addressed by the ML Certification 3 Workgroup (WG) set-up by the Institut de Recherche Technologique Saint Exup\'ery de Toulouse (IRT), as part of the DEEL Project.

The sample complexity of level set approximation

We study the problem of approximating the level set of an unknown function by sequentially querying its values. We introduce a family of algorithms called Bisect and Approximate through which we reduce the level set approximation problem to a local function approximation problem. We then show how this approach leads to rate-optimal sample complexity guarantees for H{\"o}lder functions, and we investigate how such rates improve when additional smoothness or other structural assumptions hold true.

Diversity-Preserving K-Armed Bandits, Revisited

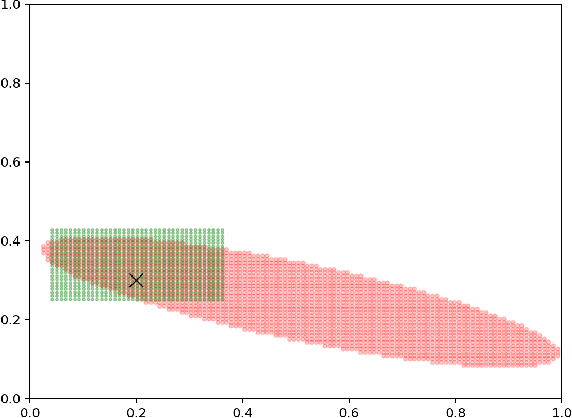
We consider the bandit-based framework for diversity-preserving recommendations introduced by Celis et al. (2019), who approached it mainly by a reduction to the setting of linear bandits. We design a UCB algorithm using the specific structure of the setting and show that it enjoys a bounded distribution-dependent regret in the natural cases when the optimal mixed actions put some probability mass on all actions (i.e., when diversity is desirable). Simulations illustrate this fact. We also provide regret lower bounds and briefly discuss distribution-free regret bounds.

Regret analysis of the Piyavskii-Shubert algorithm for global Lipschitz optimization

We consider the problem of maximizing a non-concave Lipschitz multivariate function f over a compact domain. We provide regret guarantees (i.e., optimization error bounds) for a very natural algorithm originally designed by Piyavskii and Shubert in 1972. Our results hold in a general setting in which values of f can only be accessed approximately. In particular, they yield state-of-the-art regret bounds both when f is observed exactly and when evaluations are perturbed by an independent subgaussian noise.