Conformal Prediction for Image Segmentation Using Morphological Prediction Sets

Image segmentation is a challenging task influenced by multiple sources of uncertainty, such as the data labeling process or the sampling of training data. In this paper we focus on binary segmentation and address these challenges using conformal prediction, a family of model- and data-agnostic methods for uncertainty quantification that provide finite-sample theoretical guarantees and applicable to any pretrained predictor. Our approach involves computing nonconformity scores, a type of prediction residual, on held-out calibration data not used during training. We use dilation, one of the fundamental operations in mathematical morphology, to construct a margin added to the borders of predicted segmentation masks. At inference, the predicted set formed by the mask and its margin contains the ground-truth mask with high probability, at a confidence level specified by the user. The size of the margin serves as an indicator of predictive uncertainty for a given model and dataset. We work in a regime of minimal information as we do not require any feedback from the predictor: only the predicted masks are needed for computing the prediction sets. Hence, our method is applicable to any segmentation model, including those based on deep learning; we evaluate our approach on several medical imaging applications.

Confident Object Detection via Conformal Prediction and Conformal Risk Control: an Application to Railway Signaling

Deploying deep learning models in real-world certified systems requires the ability to provide confidence estimates that accurately reflect their uncertainty. In this paper, we demonstrate the use of the conformal prediction framework to construct reliable and trustworthy predictors for detecting railway signals. Our approach is based on a novel dataset that includes images taken from the perspective of a train operator and state-of-the-art object detectors. We test several conformal approaches and introduce a new method based on conformal risk control. Our findings demonstrate the potential of the conformal prediction framework to evaluate model performance and provide practical guidance for achieving formally guaranteed uncertainty bounds.

Conformal Prediction for Trustworthy Detection of Railway Signals

We present an application of conformal prediction, a form of uncertainty quantification with guarantees, to the detection of railway signals. State-of-the-art architectures are tested and the most promising one undergoes the process of conformalization, where a correction is applied to the predicted bounding boxes (i.e. to their height and width) such that they comply with a predefined probability of success. We work with a novel exploratory dataset of images taken from the perspective of a train operator, as a first step to build and validate future trustworthy machine learning models for the detection of railway signals.

Learning to Handle Parameter Perturbations in Combinatorial Optimization: an Application to Facility Location

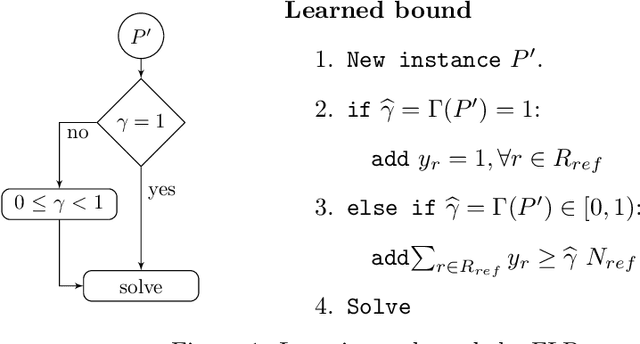
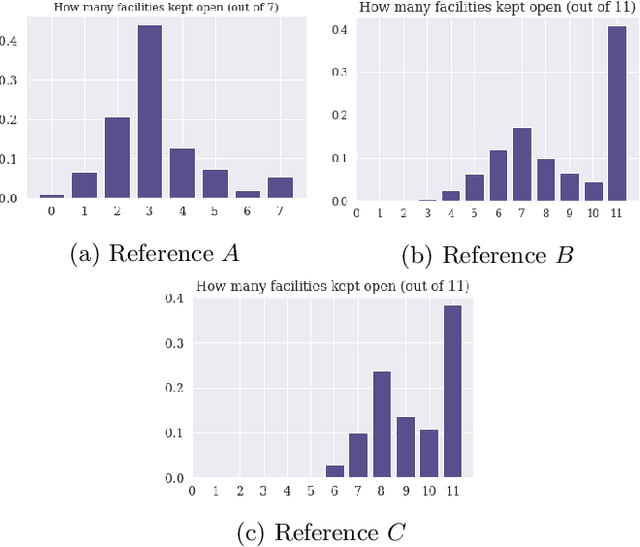
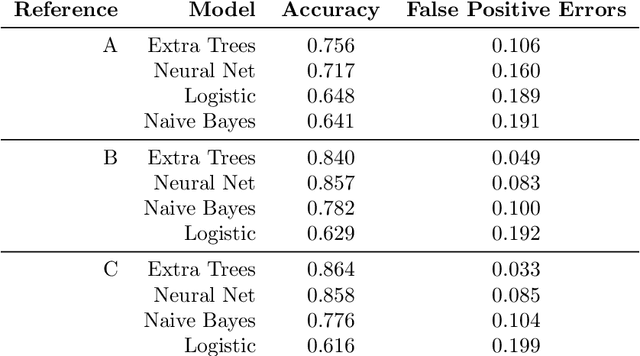
We present an approach to couple the resolution of Combinatorial Optimization problems with methods from Machine Learning, applied to the single source, capacitated, facility location problem. Our study is framed in the context where a reference facility location optimization problem is given. Assuming there exist data for many variations of the reference problem (historical or simulated) along with their optimal solution, we study how one can exploit these to make predictions about an unseen new instance. We demonstrate how a classifier can be built from these data to determine whether the solution to the reference problem still applies to a new instance. In case the reference solution is partially applicable, we build a regressor indicating the magnitude of the expected change, and conversely how much of it can be kept for the new instance. This insight, derived from a priori information, is expressed via an additional constraint in the original mathematical programming formulation. We present an empirical evaluation and discuss the benefits, drawbacks and perspectives of such an approach. Although presented through the application to the facility location problem, the approach developed here is general and explores a new perspective on the exploitation of past experience in combinatorial optimization.

A Reinforcement Learning Perspective on the Optimal Control of Mutation Probabilities for the (1+1) Evolutionary Algorithm: First Results on the OneMax Problem

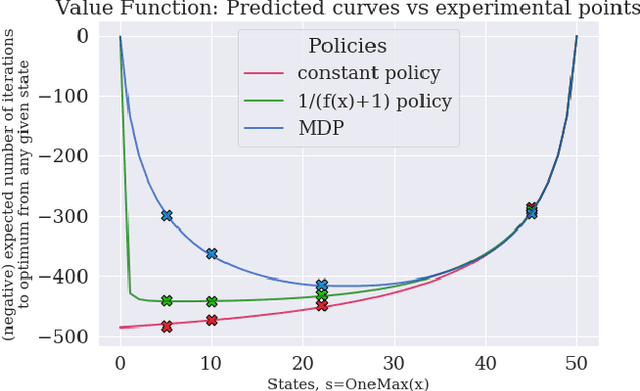
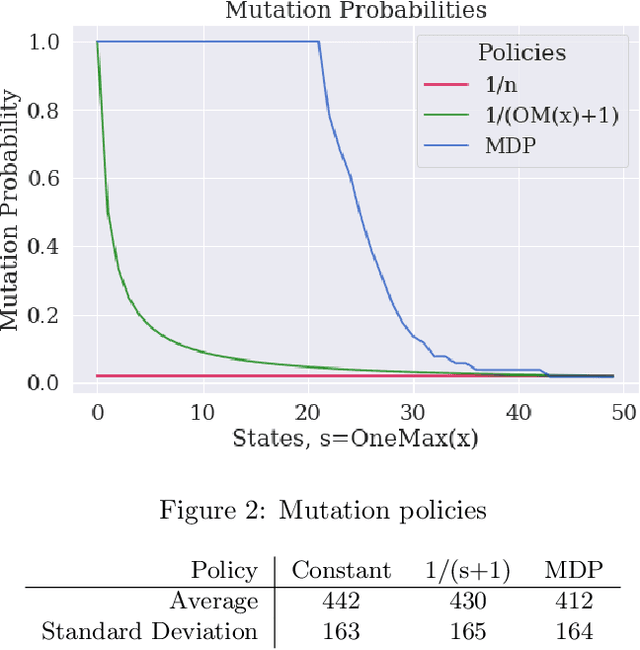
We study how Reinforcement Learning can be employed to optimally control parameters in evolutionary algorithms. We control the mutation probability of a (1+1) evolutionary algorithm on the OneMax function. This problem is modeled as a Markov Decision Process and solved with Value Iteration via the known transition probabilities. It is then solved via Q-Learning, a Reinforcement Learning algorithm, where the exact transition probabilities are not needed. This approach also allows previous expert or empirical knowledge to be included into learning. It opens new perspectives, both formally and computationally, for the problem of parameter control in optimization.

Naive Bayes Classification for Subset Selection

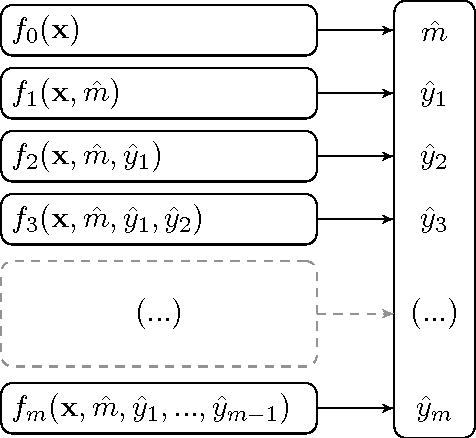
This article focuses on the question of learning how to automatically select a subset of items among a bigger set. We introduce a methodology for the inference of ensembles of discrete values, based on the Naive Bayes assumption. Our motivation stems from practical use cases where one wishes to predict an unordered set of (possibly interdependent) values from a set of observed features. This problem can be considered in the context of Multi-label Classification (MLC) where such values are seen as labels associated to continuous or discrete features. We introduce the \nbx algorithm, an extension of Naive Bayes classification into the multi-label domain, discuss its properties and evaluate our approach on real-world problems.