Learning to Handle Parameter Perturbations in Combinatorial Optimization: an Application to Facility Location
Paper and Code
Jul 12, 2019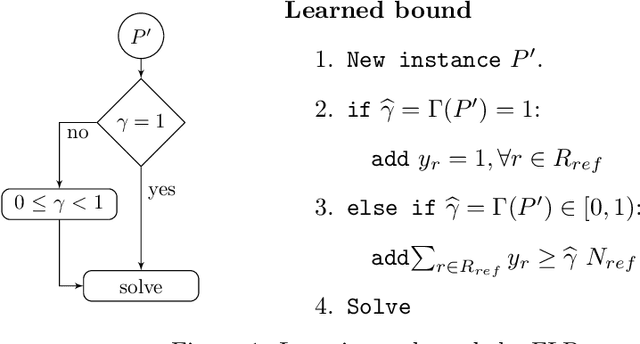

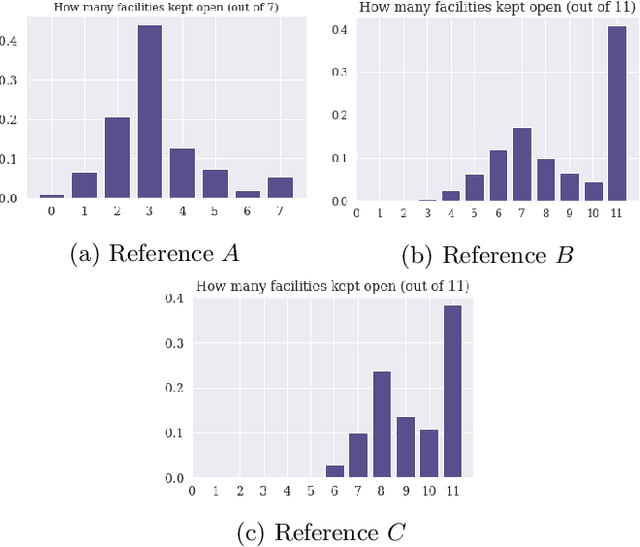
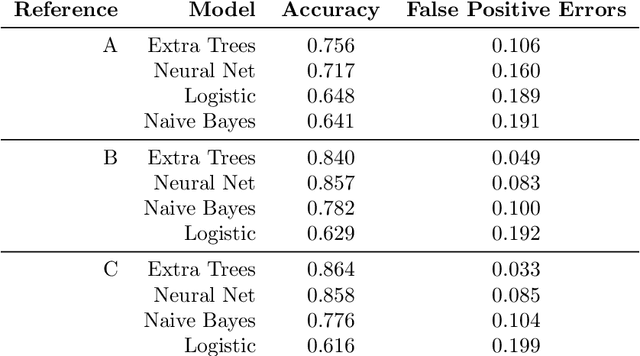
We present an approach to couple the resolution of Combinatorial Optimization problems with methods from Machine Learning, applied to the single source, capacitated, facility location problem. Our study is framed in the context where a reference facility location optimization problem is given. Assuming there exist data for many variations of the reference problem (historical or simulated) along with their optimal solution, we study how one can exploit these to make predictions about an unseen new instance. We demonstrate how a classifier can be built from these data to determine whether the solution to the reference problem still applies to a new instance. In case the reference solution is partially applicable, we build a regressor indicating the magnitude of the expected change, and conversely how much of it can be kept for the new instance. This insight, derived from a priori information, is expressed via an additional constraint in the original mathematical programming formulation. We present an empirical evaluation and discuss the benefits, drawbacks and perspectives of such an approach. Although presented through the application to the facility location problem, the approach developed here is general and explores a new perspective on the exploitation of past experience in combinatorial optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge