A second-order-like optimizer with adaptive gradient scaling for deep learning

In this empirical article, we introduce INNAprop, an optimization algorithm that combines the INNA method with the RMSprop adaptive gradient scaling. It leverages second-order information and rescaling while keeping the memory requirements of standard DL methods as AdamW or SGD with momentum.After having recalled our geometrical motivations, we provide quite extensive experiments. On image classification (CIFAR-10, ImageNet) and language modeling (GPT-2), INNAprop consistently matches or outperforms AdamW both in training speed and accuracy, with minimal hyperparameter tuning in large-scale settings. Our code is publicly available at \url{https://github.com/innaprop/innaprop}.

Inexact subgradient methods for semialgebraic functions

Motivated by the widespread use of approximate derivatives in machine learning and optimization, we study inexact subgradient methods with non-vanishing additive errors and step sizes. In the nonconvex semialgebraic setting, under boundedness assumptions, we prove that the method provides points that eventually fluctuate close to the critical set at a distance proportional to $\epsilon^\rho$ where $\epsilon$ is the error in subgradient evaluation and $\rho$ relates to the geometry of the problem. In the convex setting, we provide complexity results for the averaged values. We also obtain byproducts of independent interest, such as descent-like lemmas for nonsmooth nonconvex problems and some results on the limit of affine interpolants of differential inclusions.

One-step differentiation of iterative algorithms

In appropriate frameworks, automatic differentiation is transparent to the user at the cost of being a significant computational burden when the number of operations is large. For iterative algorithms, implicit differentiation alleviates this issue but requires custom implementation of Jacobian evaluation. In this paper, we study one-step differentiation, also known as Jacobian-free backpropagation, a method as easy as automatic differentiation and as performant as implicit differentiation for fast algorithms (e.g., superlinear optimization methods). We provide a complete theoretical approximation analysis with specific examples (Newton's method, gradient descent) along with its consequences in bilevel optimization. Several numerical examples illustrate the well-foundness of the one-step estimator.

Differentiating Nonsmooth Solutions to Parametric Monotone Inclusion Problems

We leverage path differentiability and a recent result on nonsmooth implicit differentiation calculus to give sufficient conditions ensuring that the solution to a monotone inclusion problem will be path differentiable, with formulas for computing its generalized gradient. A direct consequence of our result is that these solutions happen to be differentiable almost everywhere. Our approach is fully compatible with automatic differentiation and comes with assumptions which are easy to check, roughly speaking: semialgebraicity and strong monotonicity. We illustrate the scope of our results by considering three fundamental composite problem settings: strongly convex problems, dual solutions to convex minimization problems and primal-dual solutions to min-max problems.

Nonsmooth automatic differentiation: a cheap gradient principle and other complexity results

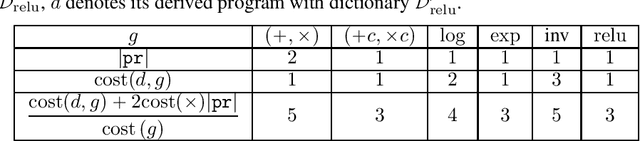
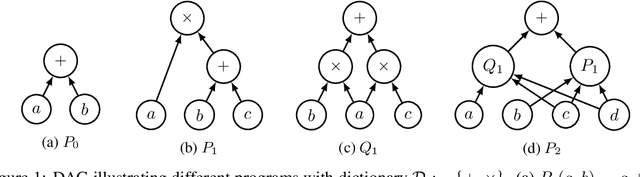
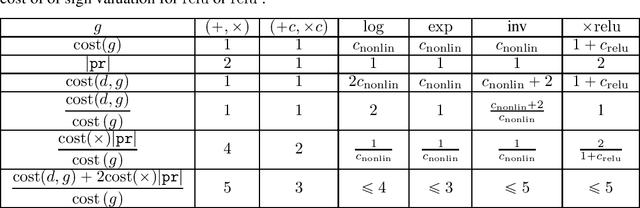
We provide a simple model to estimate the computational costs of the backward and forward modes of algorithmic differentiation for a wide class of nonsmooth programs. Prominent examples are the famous relu and convolutional neural networks together with their standard loss functions. Using the recent notion of conservative gradients, we then establish a "nonsmooth cheap gradient principle" for backpropagation encompassing most concrete applications. Nonsmooth backpropagation's cheapness contrasts with concurrent forward approaches which have, at this day, dimensional-dependent worst case estimates. In order to understand this class of methods, we relate the complexity of computing a large number of directional derivatives to that of matrix multiplication. This shows a fundamental limitation for improving forward AD for that task. Finally, while the fastest algorithms for computing a Clarke subgradient are linear in the dimension, it appears that computing two distinct Clarke (resp. lexicographic) subgradients for simple neural networks is NP-Hard.

Automatic differentiation of nonsmooth iterative algorithms

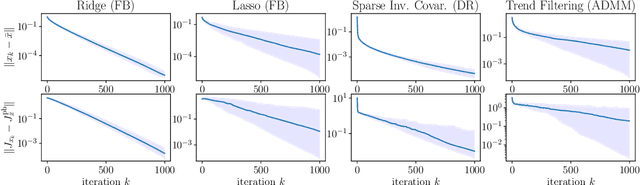
Differentiation along algorithms, i.e., piggyback propagation of derivatives, is now routinely used to differentiate iterative solvers in differentiable programming. Asymptotics is well understood for many smooth problems but the nondifferentiable case is hardly considered. Is there a limiting object for nonsmooth piggyback automatic differentiation (AD)? Does it have any variational meaning and can it be used effectively in machine learning? Is there a connection with classical derivative? All these questions are addressed under appropriate nonexpansivity conditions in the framework of conservative derivatives which has proved useful in understanding nonsmooth AD. For nonsmooth piggyback iterations, we characterize the attractor set of nonsmooth piggyback iterations as a set-valued fixed point which remains in the conservative framework. This has various consequences and in particular almost everywhere convergence of classical derivatives. Our results are illustrated on parametric convex optimization problems with forward-backward, Douglas-Rachford and Alternating Direction of Multiplier algorithms as well as the Heavy-Ball method.

Numerical influence of ReLU'(0) on backpropagation

In theory, the choice of ReLU'(0) in [0, 1] for a neural network has a negligible influence both on backpropagation and training. Yet, in the real world, 32 bits default precision combined with the size of deep learning problems makes it a hyperparameter of training methods. We investigate the importance of the value of ReLU'(0) for several precision levels (16, 32, 64 bits), on various networks (fully connected, VGG, ResNet) and datasets (MNIST, CIFAR10, SVHN). We observe considerable variations of backpropagation outputs which occur around half of the time in 32 bits precision. The effect disappears with double precision, while it is systematic at 16 bits. For vanilla SGD training, the choice ReLU'(0) = 0 seems to be the most efficient. We also evidence that reconditioning approaches as batch-norm or ADAM tend to buffer the influence of ReLU'(0)'s value. Overall, the message we want to convey is that algorithmic differentiation of nonsmooth problems potentially hides parameters that could be tuned advantageously.

Nonsmooth Implicit Differentiation for Machine Learning and Optimization

In view of training increasingly complex learning architectures, we establish a nonsmooth implicit function theorem with an operational calculus. Our result applies to most practical problems (i.e., definable problems) provided that a nonsmooth form of the classical invertibility condition is fulfilled. This approach allows for formal subdifferentiation: for instance, replacing derivatives by Clarke Jacobians in the usual differentiation formulas is fully justified for a wide class of nonsmooth problems. Moreover this calculus is entirely compatible with algorithmic differentiation (e.g., backpropagation). We provide several applications such as training deep equilibrium networks, training neural nets with conic optimization layers, or hyperparameter-tuning for nonsmooth Lasso-type models. To show the sharpness of our assumptions, we present numerical experiments showcasing the extremely pathological gradient dynamics one can encounter when applying implicit algorithmic differentiation without any hypothesis.

Second-order step-size tuning of SGD for non-convex optimization

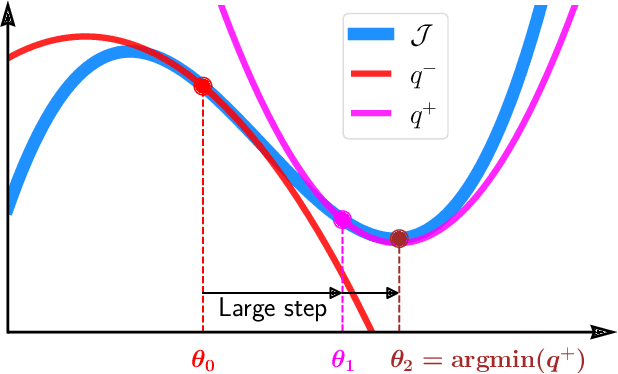
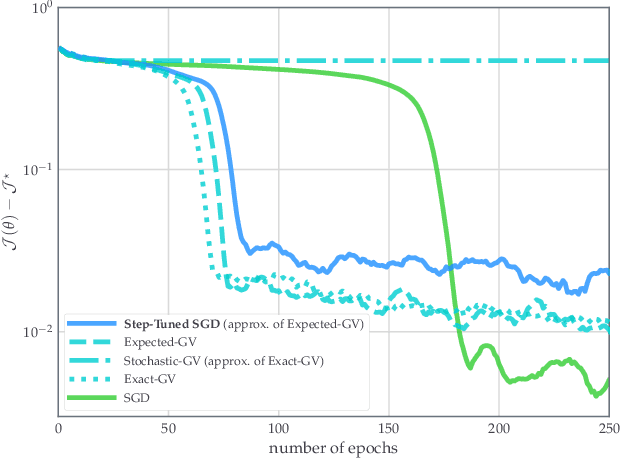
In view of a direct and simple improvement of vanilla SGD, this paper presents a fine-tuning of its step-sizes in the mini-batch case. For doing so, one estimates curvature, based on a local quadratic model and using only noisy gradient approximations. One obtains a new stochastic first-order method (Step-Tuned SGD) which can be seen as a stochastic version of the classical Barzilai-Borwein method. Our theoretical results ensure almost sure convergence to the critical set and we provide convergence rates. Experiments on deep residual network training illustrate the favorable properties of our approach. For such networks we observe, during training, both a sudden drop of the loss and an improvement of test accuracy at medium stages, yielding better results than SGD, RMSprop, or ADAM.

A Hölderian backtracking method for min-max and min-min problems

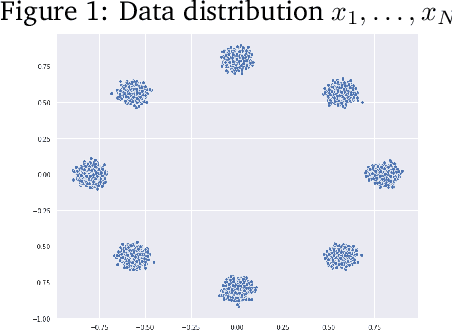
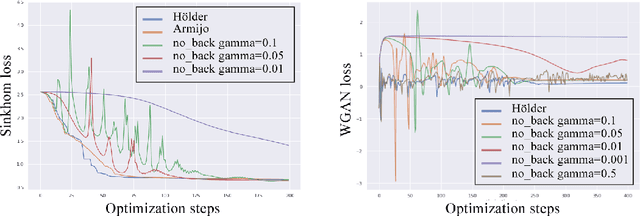
We present a new algorithm to solve min-max or min-min problems out of the convex world. We use rigidity assumptions, ubiquitous in learning, making our method applicable to many optimization problems. Our approach takes advantage of hidden regularity properties and allows us to devise a simple algorithm of ridge type. An original feature of our method is to come with automatic step size adaptation which departs from the usual overly cautious backtracking methods. In a general framework, we provide convergence theoretical guarantees and rates. We apply our findings on simple GAN problems obtaining promising numerical results.