Stochastic Adaptive Gradient Descent Without Descent

We introduce a new adaptive step-size strategy for convex optimization with stochastic gradient that exploits the local geometry of the objective function only by means of a first-order stochastic oracle and without any hyper-parameter tuning. The method comes from a theoretically-grounded adaptation of the Adaptive Gradient Descent Without Descent method to the stochastic setting. We prove the convergence of stochastic gradient descent with our step-size under various assumptions, and we show that it empirically competes against tuned baselines.

From Learning to Optimize to Learning Optimization Algorithms

Towards designing learned optimization algorithms that are usable beyond their training setting, we identify key principles that classical algorithms obey, but have up to now, not been used for Learning to Optimize (L2O). Following these principles, we provide a general design pipeline, taking into account data, architecture and learning strategy, and thereby enabling a synergy between classical optimization and L2O, resulting in a philosophy of Learning Optimization Algorithms. As a consequence our learned algorithms perform well far beyond problems from the training distribution. We demonstrate the success of these novel principles by designing a new learning-enhanced BFGS algorithm and provide numerical experiments evidencing its adaptation to many settings at test time.

Near-optimal Closed-loop Method via Lyapunov Damping for Convex Optimization

We introduce an autonomous system with closed-loop damping for first-order convex optimization. While, to this day, optimal rates of convergence are only achieved by non-autonomous methods via open-loop damping (e.g., Nesterov's algorithm), we show that our system is the first one featuring a closed-loop damping while exhibiting a rate arbitrarily close to the optimal one. We do so by coupling the damping and the speed of convergence of the system via a well-chosen Lyapunov function. We then derive a practical first-order algorithm called LYDIA by discretizing our system, and present numerical experiments supporting our theoretical findings.

Inertial Newton Algorithms Avoiding Strict Saddle Points

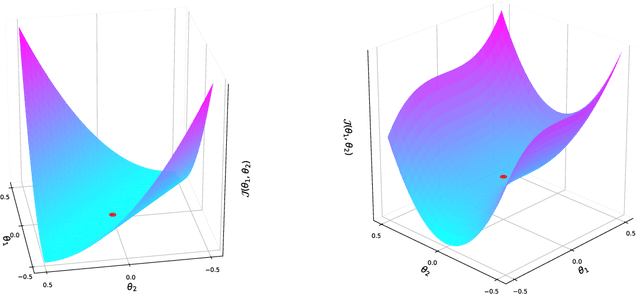
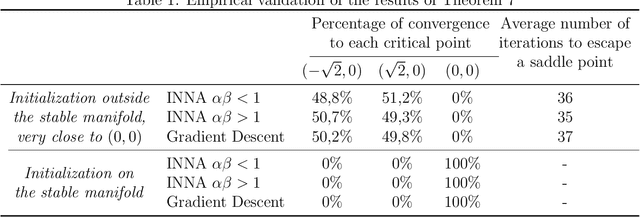
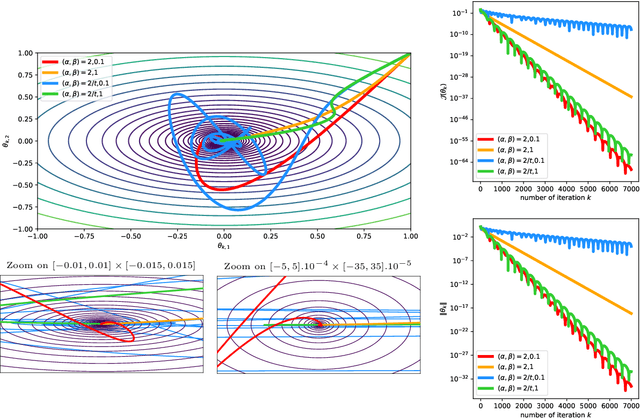
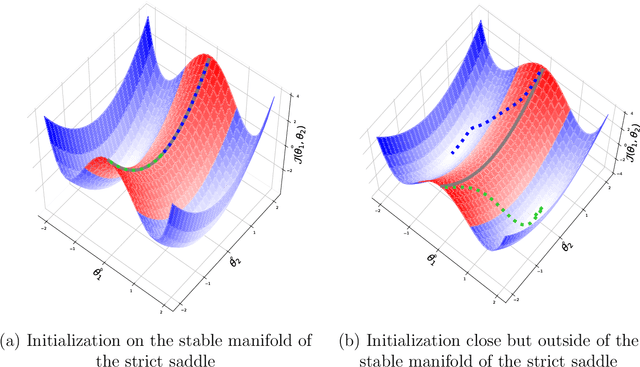
We study the asymptotic behavior of second-order algorithms mixing Newton's method and inertial gradient descent in non-convex landscapes. We show that, despite the Newtonian behavior of these methods, they almost always escape strict saddle points. We also evidence the role played by the hyper-parameters of these methods in their qualitative behavior near critical points. The theoretical results are supported by numerical illustrations.

Second-order step-size tuning of SGD for non-convex optimization

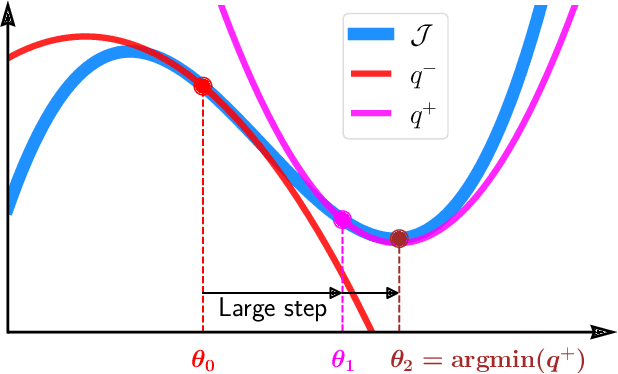
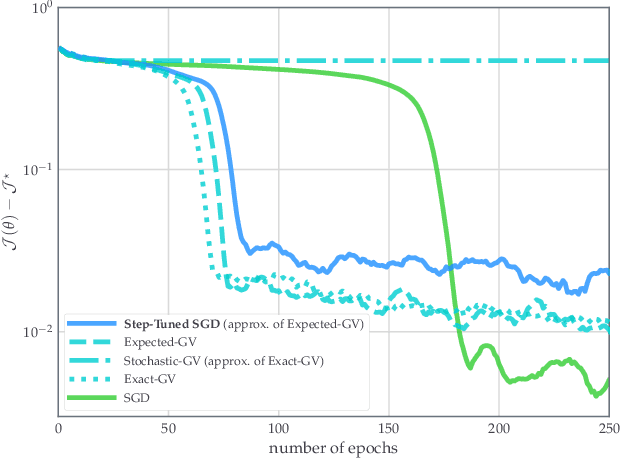
In view of a direct and simple improvement of vanilla SGD, this paper presents a fine-tuning of its step-sizes in the mini-batch case. For doing so, one estimates curvature, based on a local quadratic model and using only noisy gradient approximations. One obtains a new stochastic first-order method (Step-Tuned SGD) which can be seen as a stochastic version of the classical Barzilai-Borwein method. Our theoretical results ensure almost sure convergence to the critical set and we provide convergence rates. Experiments on deep residual network training illustrate the favorable properties of our approach. For such networks we observe, during training, both a sudden drop of the loss and an improvement of test accuracy at medium stages, yielding better results than SGD, RMSprop, or ADAM.

An Inertial Newton Algorithm for Deep Learning

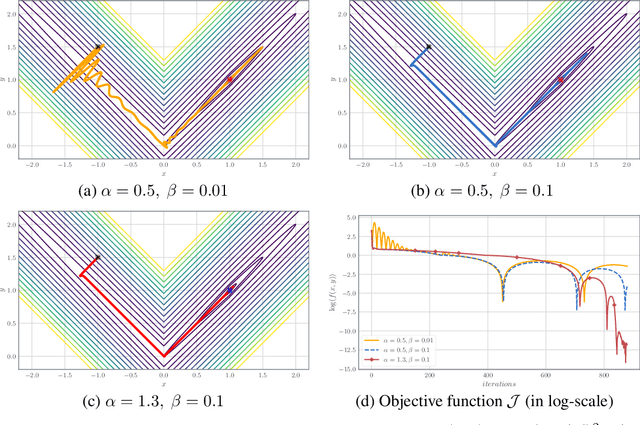
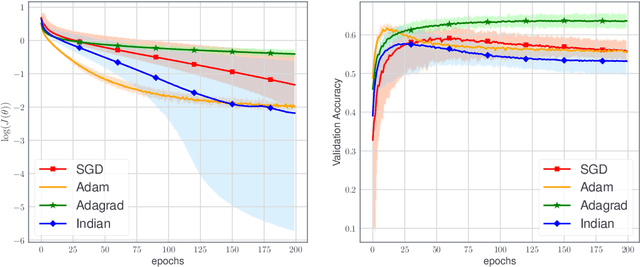
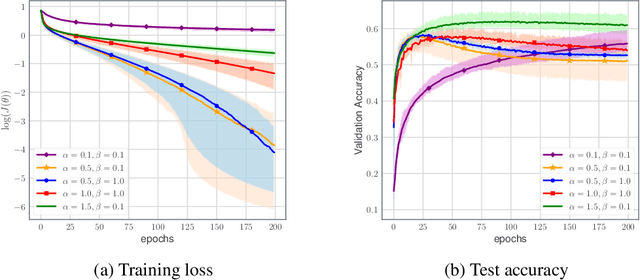
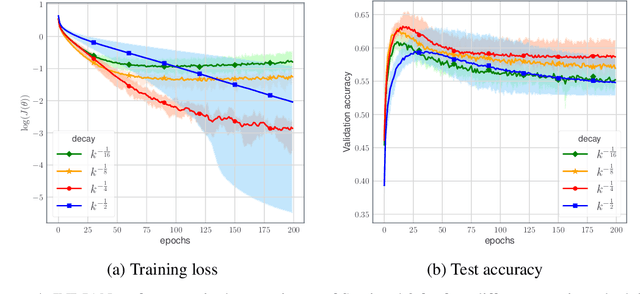
We devise a learning algorithm for possibly nonsmooth deep neural networks featuring inertia and Newtonian directional intelligence only by means of a back-propagation oracle. Our algorithm, called INDIAN, has an appealing mechanical interpretation, making the role of its two hyperparameters transparent. An elementary phase space lifting allows both for its implementation and its theoretical study under very general assumptions. We handle in particular a stochastic version of our method (which encompasses usual mini-batch approaches) for nonsmooth activation functions (such as ReLU). Our algorithm shows high efficiency and reaches state of the art on image classification problems.