Second-order step-size tuning of SGD for non-convex optimization
Paper and Code
Mar 05, 2021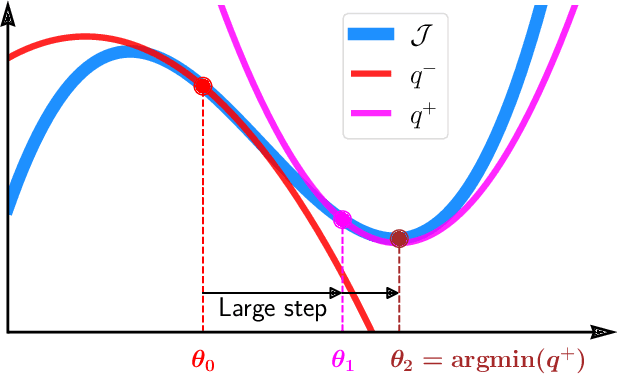
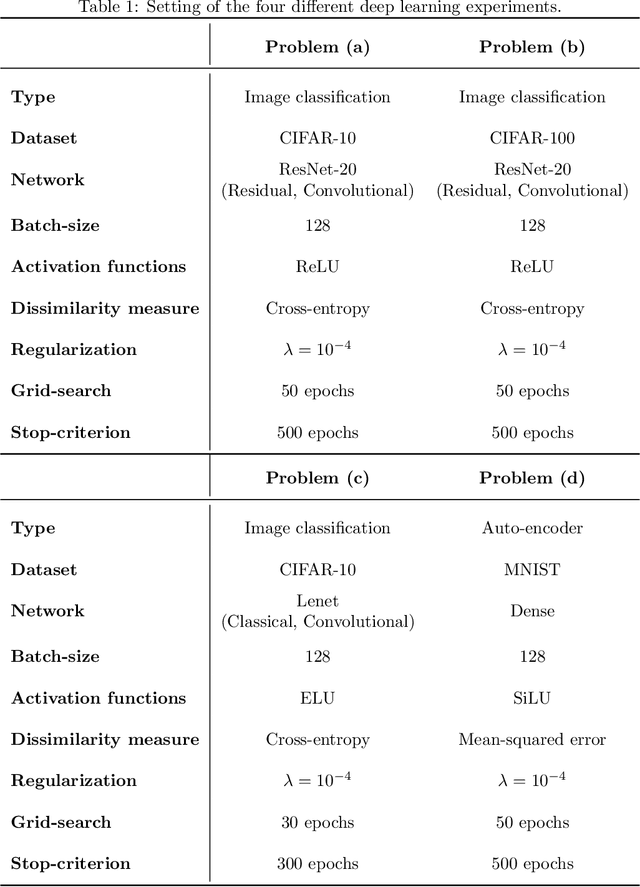

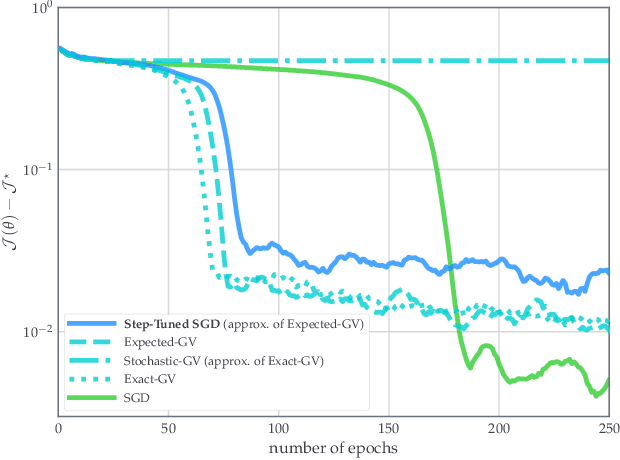
In view of a direct and simple improvement of vanilla SGD, this paper presents a fine-tuning of its step-sizes in the mini-batch case. For doing so, one estimates curvature, based on a local quadratic model and using only noisy gradient approximations. One obtains a new stochastic first-order method (Step-Tuned SGD) which can be seen as a stochastic version of the classical Barzilai-Borwein method. Our theoretical results ensure almost sure convergence to the critical set and we provide convergence rates. Experiments on deep residual network training illustrate the favorable properties of our approach. For such networks we observe, during training, both a sudden drop of the loss and an improvement of test accuracy at medium stages, yielding better results than SGD, RMSprop, or ADAM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge