Inertial Newton Algorithms Avoiding Strict Saddle Points
Paper and Code
Nov 08, 2021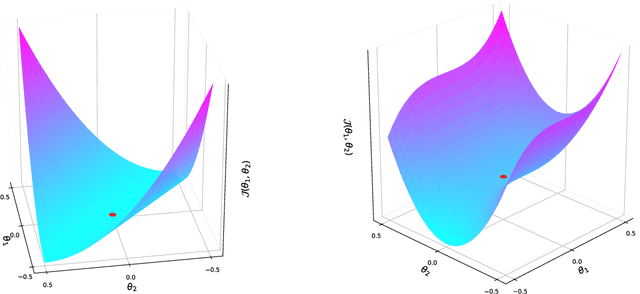
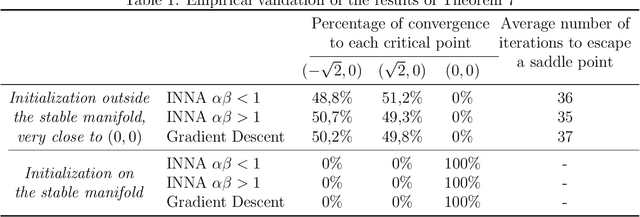
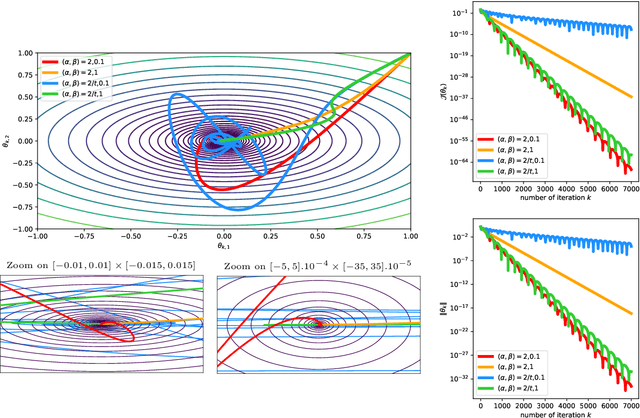
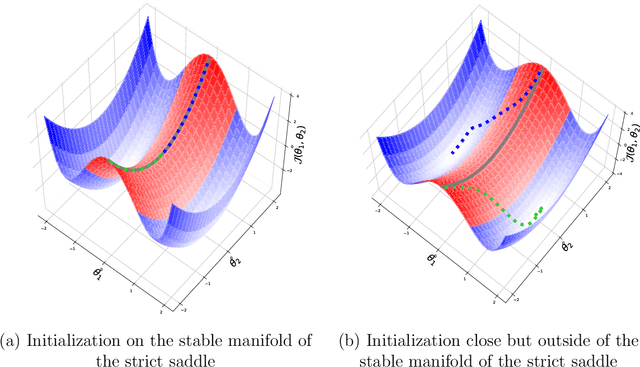
We study the asymptotic behavior of second-order algorithms mixing Newton's method and inertial gradient descent in non-convex landscapes. We show that, despite the Newtonian behavior of these methods, they almost always escape strict saddle points. We also evidence the role played by the hyper-parameters of these methods in their qualitative behavior near critical points. The theoretical results are supported by numerical illustrations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge