François Malgouyres
IMT
Quantized Approximately Orthogonal Recurrent Neural Networks
Feb 05, 2024



Abstract:Orthogonal recurrent neural networks (ORNNs) are an appealing option for learning tasks involving time series with long-term dependencies, thanks to their simplicity and computational stability. However, these networks often require a substantial number of parameters to perform well, which can be prohibitive in power-constrained environments, such as compact devices. One approach to address this issue is neural network quantization. The construction of such networks remains an open problem, acknowledged for its inherent instability.In this paper, we explore the quantization of the recurrent and input weight matrices in ORNNs, leading to Quantized approximately Orthogonal RNNs (QORNNs). We investigate one post-training quantization (PTQ) strategy and three quantization-aware training (QAT) algorithms that incorporate orthogonal constraints and quantized weights. Empirical results demonstrate the advantages of employing QAT over PTQ. The most efficient model achieves results similar to state-of-the-art full-precision ORNN and LSTM on a variety of standard benchmarks, even with 3-bits quantization.
Support Exploration Algorithm for Sparse Support Recovery
Jan 31, 2023



Abstract:We introduce a new algorithm promoting sparsity called {\it Support Exploration Algorithm (SEA)} and analyze it in the context of support recovery/model selection problems.The algorithm can be interpreted as an instance of the {\it straight-through estimator (STE)} applied to the resolution of a sparse linear inverse problem. SEA uses a non-sparse exploratory vector and makes it evolve in the input space to select the sparse support. We put to evidence an oracle update rule for the exploratory vector and consider the STE update. The theoretical analysis establishes general sufficient conditions of support recovery. The general conditions are specialized to the case where the matrix $A$ performing the linear measurements satisfies the {\it Restricted Isometry Property (RIP)}.Experiments show that SEA can efficiently improve the results of any algorithm. Because of its exploratory nature, SEA also performs remarkably well when the columns of $A$ are strongly coherent.
Local Identifiability of Deep ReLU Neural Networks: the Theory
Jun 15, 2022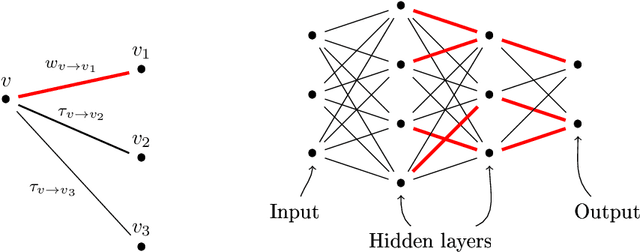


Abstract:Is a sample rich enough to determine, at least locally, the parameters of a neural network? To answer this question, we introduce a new local parameterization of a given deep ReLU neural network by fixing the values of some of its weights. This allows us to define local lifting operators whose inverses are charts of a smooth manifold of a high dimensional space. The function implemented by the deep ReLU neural network composes the local lifting with a linear operator which depends on the sample. We derive from this convenient representation a geometrical necessary and sufficient condition of local identifiability. Looking at tangent spaces, the geometrical condition provides: 1/ a sharp and testable necessary condition of identifiability and 2/ a sharp and testable sufficient condition of local identifiability. The validity of the conditions can be tested numerically using backpropagation and matrix rank computations.
A general approximation lower bound in $L^p$ norm, with applications to feed-forward neural networks
Jun 09, 2022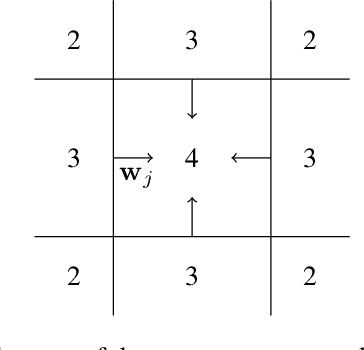

Abstract:We study the fundamental limits to the expressive power of neural networks. Given two sets $F$, $G$ of real-valued functions, we first prove a general lower bound on how well functions in $F$ can be approximated in $L^p(\mu)$ norm by functions in $G$, for any $p \geq 1$ and any probability measure $\mu$. The lower bound depends on the packing number of $F$, the range of $F$, and the fat-shattering dimension of $G$. We then instantiate this bound to the case where $G$ corresponds to a piecewise-polynomial feed-forward neural network, and describe in details the application to two sets $F$: H{\"o}lder balls and multivariate monotonic functions. Beside matching (known or new) upper bounds up to log factors, our lower bounds shed some light on the similarities or differences between approximation in $L^p$ norm or in sup norm, solving an open question by DeVore et al. (2021). Our proof strategy differs from the sup norm case and uses a key probability result of Mendelson (2002).
Parameter identifiability of a deep feedforward ReLU neural network
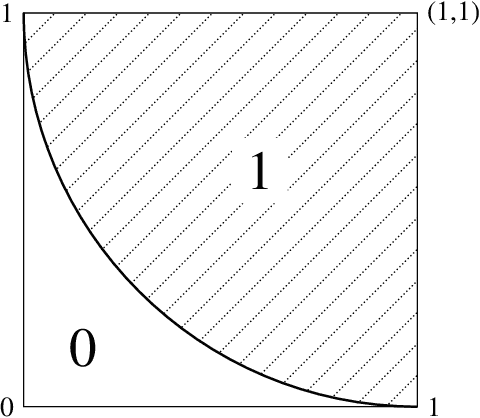
Dec 24, 2021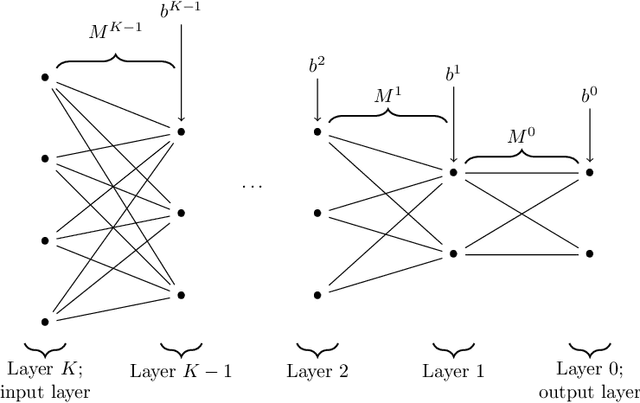
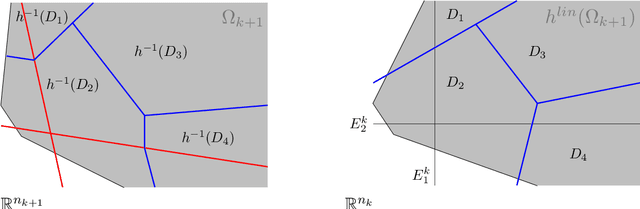
Abstract:The possibility for one to recover the parameters-weights and biases-of a neural network thanks to the knowledge of its function on a subset of the input space can be, depending on the situation, a curse or a blessing. On one hand, recovering the parameters allows for better adversarial attacks and could also disclose sensitive information from the dataset used to construct the network. On the other hand, if the parameters of a network can be recovered, it guarantees the user that the features in the latent spaces can be interpreted. It also provides foundations to obtain formal guarantees on the performances of the network. It is therefore important to characterize the networks whose parameters can be identified and those whose parameters cannot. In this article, we provide a set of conditions on a deep fully-connected feedforward ReLU neural network under which the parameters of the network are uniquely identified-modulo permutation and positive rescaling-from the function it implements on a subset of the input space.
Overestimation learning with guarantees
Jan 26, 2021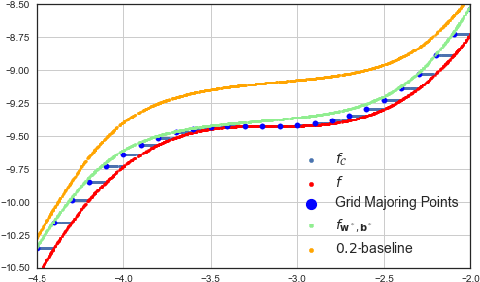
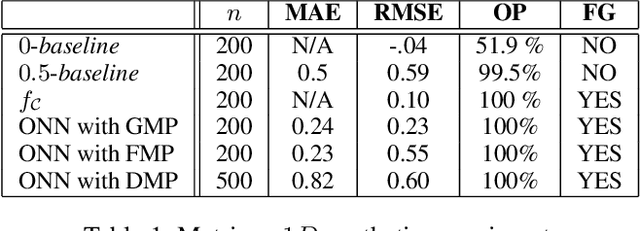
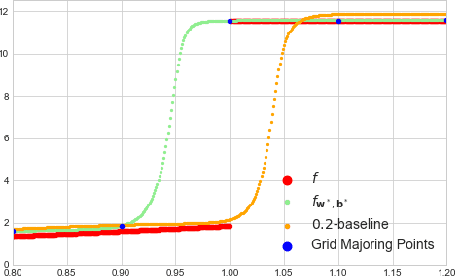
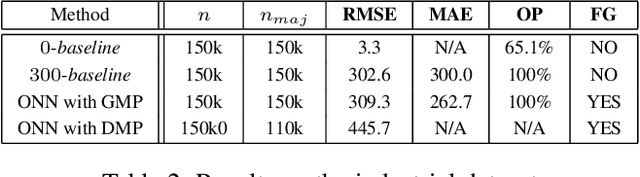
Abstract:We describe a complete method that learns a neural network which is guaranteed to overestimate a reference function on a given domain. The neural network can then be used as a surrogate for the reference function. The method involves two steps. In the first step, we construct an adaptive set of Majoring Points. In the second step, we optimize a well-chosen neural network to overestimate the Majoring Points. In order to extend the guarantee on the Majoring Points to the whole domain, we necessarily have to make an assumption on the reference function. In this study, we assume that the reference function is monotonic. We provide experiments on synthetic and real problems. The experiments show that the density of the Majoring Points concentrate where the reference function varies. The learned over-estimations are both guaranteed to overestimate the reference function and are proven empirically to provide good approximations of it. Experiments on real data show that the method makes it possible to use the surrogate function in embedded systems for which an underestimation is critical; when computing the reference function requires too many resources.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge