Unveiling and Mitigating Adversarial Vulnerabilities in Iterative Optimizers

Machine learning (ML) models are often sensitive to carefully crafted yet seemingly unnoticeable perturbations. Such adversarial examples are considered to be a property of ML models, often associated with their black-box operation and sensitivity to features learned from data. This work examines the adversarial sensitivity of non-learned decision rules, and particularly of iterative optimizers. Our analysis is inspired by the recent developments in deep unfolding, which cast such optimizers as ML models. We show that non-learned iterative optimizers share the sensitivity to adversarial examples of ML models, and that attacking iterative optimizers effectively alters the optimization objective surface in a manner that modifies the minima sought. We then leverage the ability to cast iteration-limited optimizers as ML models to enhance robustness via adversarial training. For a class of proximal gradient optimizers, we rigorously prove how their learning affects adversarial sensitivity. We numerically back our findings, showing the vulnerability of various optimizers, as well as the robustness induced by unfolding and adversarial training.

Deep Unrolling for Nonconvex Robust Principal Component Analysis

We design algorithms for Robust Principal Component Analysis (RPCA) which consists in decomposing a matrix into the sum of a low rank matrix and a sparse matrix. We propose a deep unrolled algorithm based on an accelerated alternating projection algorithm which aims to solve RPCA in its nonconvex form. The proposed procedure combines benefits of deep neural networks and the interpretability of the original algorithm and it automatically learns hyperparameters. We demonstrate the unrolled algorithm's effectiveness on synthetic datasets and also on a face modeling problem, where it leads to both better numerical and visual performances.

Support Exploration Algorithm for Sparse Support Recovery

We introduce a new algorithm promoting sparsity called {\it Support Exploration Algorithm (SEA)} and analyze it in the context of support recovery/model selection problems.The algorithm can be interpreted as an instance of the {\it straight-through estimator (STE)} applied to the resolution of a sparse linear inverse problem. SEA uses a non-sparse exploratory vector and makes it evolve in the input space to select the sparse support. We put to evidence an oracle update rule for the exploratory vector and consider the STE update. The theoretical analysis establishes general sufficient conditions of support recovery. The general conditions are specialized to the case where the matrix $A$ performing the linear measurements satisfies the {\it Restricted Isometry Property (RIP)}.Experiments show that SEA can efficiently improve the results of any algorithm. Because of its exploratory nature, SEA also performs remarkably well when the columns of $A$ are strongly coherent.

Image Analysis Using a Dual-Tree $M$-Band Wavelet Transform

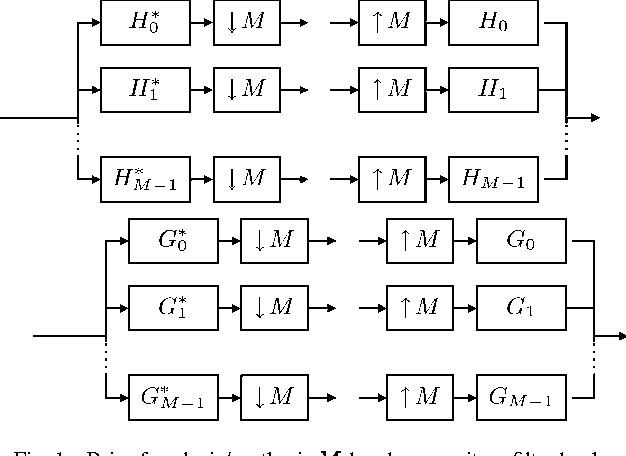
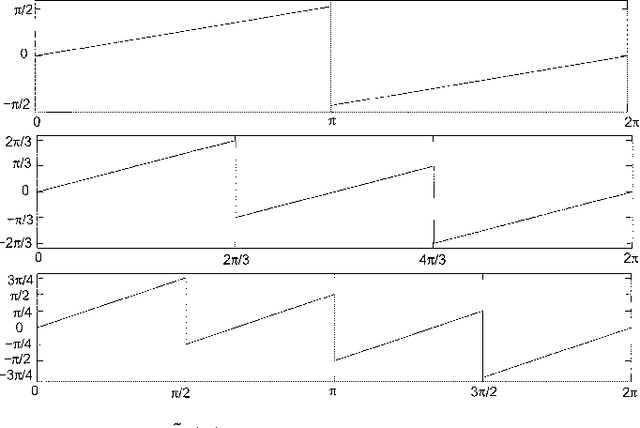
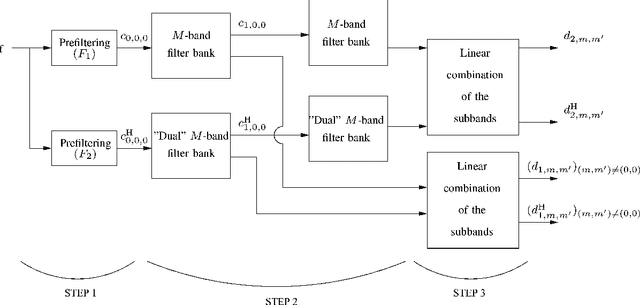
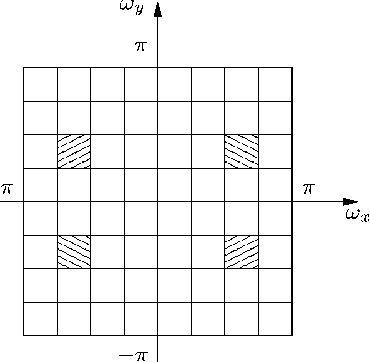
We propose a 2D generalization to the $M$-band case of the dual-tree decomposition structure (initially proposed by N. Kingsbury and further investigated by I. Selesnick) based on a Hilbert pair of wavelets. We particularly address (\textit{i}) the construction of the dual basis and (\textit{ii}) the resulting directional analysis. We also revisit the necessary pre-processing stage in the $M$-band case. While several reconstructions are possible because of the redundancy of the representation, we propose a new optimal signal reconstruction technique, which minimizes potential estimation errors. The effectiveness of the proposed $M$-band decomposition is demonstrated via denoising comparisons on several image types (natural, texture, seismics), with various $M$-band wavelets and thresholding strategies. Significant improvements in terms of both overall noise reduction and direction preservation are observed.

Noise Covariance Properties in Dual-Tree Wavelet Decompositions

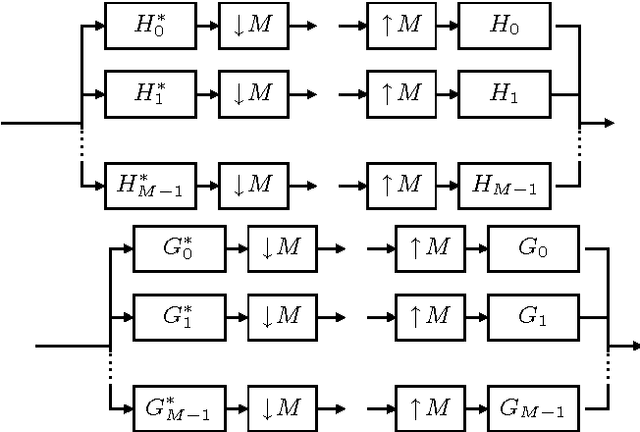
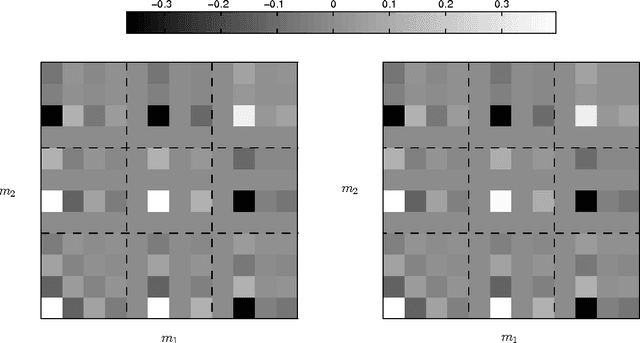
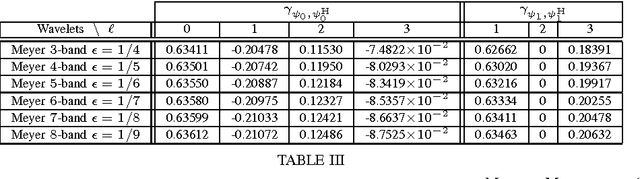
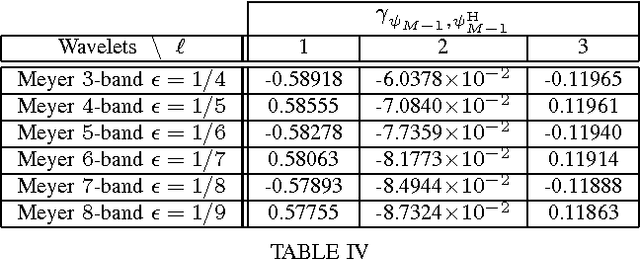
Dual-tree wavelet decompositions have recently gained much popularity, mainly due to their ability to provide an accurate directional analysis of images combined with a reduced redundancy. When the decomposition of a random process is performed -- which occurs in particular when an additive noise is corrupting the signal to be analyzed -- it is useful to characterize the statistical properties of the dual-tree wavelet coefficients of this process. As dual-tree decompositions constitute overcomplete frame expansions, correlation structures are introduced among the coefficients, even when a white noise is analyzed. In this paper, we show that it is possible to provide an accurate description of the covariance properties of the dual-tree coefficients of a wide-sense stationary process. The expressions of the (cross-)covariance sequences of the coefficients are derived in the one and two-dimensional cases. Asymptotic results are also provided, allowing to predict the behaviour of the second-order moments for large lag values or at coarse resolution. In addition, the cross-correlations between the primal and dual wavelets, which play a primary role in our theoretical analysis, are calculated for a number of classical wavelet families. Simulation results are finally provided to validate these results.

A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity

The richness of natural images makes the quest for optimal representations in image processing and computer vision challenging. The latter observation has not prevented the design of image representations, which trade off between efficiency and complexity, while achieving accurate rendering of smooth regions as well as reproducing faithful contours and textures. The most recent ones, proposed in the past decade, share an hybrid heritage highlighting the multiscale and oriented nature of edges and patterns in images. This paper presents a panorama of the aforementioned literature on decompositions in multiscale, multi-orientation bases or dictionaries. They typically exhibit redundancy to improve sparsity in the transformed domain and sometimes its invariance with respect to simple geometric deformations (translation, rotation). Oriented multiscale dictionaries extend traditional wavelet processing and may offer rotation invariance. Highly redundant dictionaries require specific algorithms to simplify the search for an efficient (sparse) representation. We also discuss the extension of multiscale geometric decompositions to non-Euclidean domains such as the sphere or arbitrary meshed surfaces. The etymology of panorama suggests an overview, based on a choice of partially overlapping "pictures". We hope that this paper will contribute to the appreciation and apprehension of a stream of current research directions in image understanding.