Image Analysis Using a Dual-Tree $M$-Band Wavelet Transform
Paper and Code
Feb 27, 2017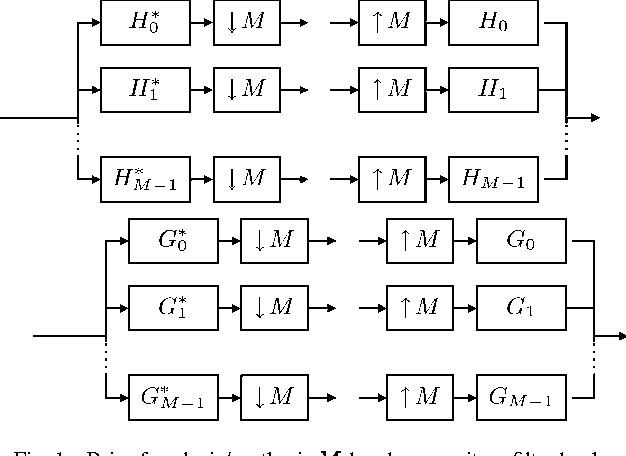
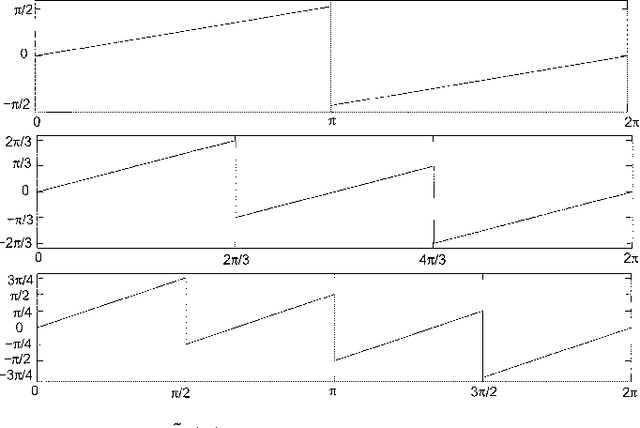
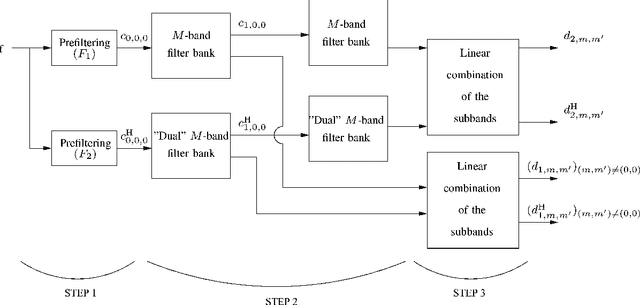
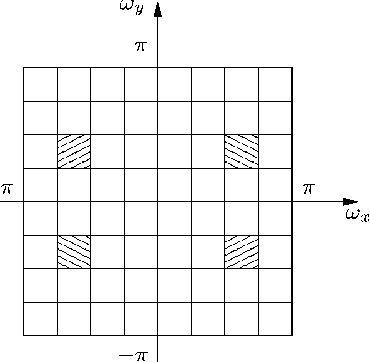
We propose a 2D generalization to the $M$-band case of the dual-tree decomposition structure (initially proposed by N. Kingsbury and further investigated by I. Selesnick) based on a Hilbert pair of wavelets. We particularly address (\textit{i}) the construction of the dual basis and (\textit{ii}) the resulting directional analysis. We also revisit the necessary pre-processing stage in the $M$-band case. While several reconstructions are possible because of the redundancy of the representation, we propose a new optimal signal reconstruction technique, which minimizes potential estimation errors. The effectiveness of the proposed $M$-band decomposition is demonstrated via denoising comparisons on several image types (natural, texture, seismics), with various $M$-band wavelets and thresholding strategies. Significant improvements in terms of both overall noise reduction and direction preservation are observed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge