Proximal Operators of Sorted Nonconvex Penalties

This work studies the problem of sparse signal recovery with automatic grouping of variables. To this end, we investigate sorted nonsmooth penalties as a regularization approach for generalized linear models. We focus on a family of sorted nonconvex penalties which generalizes the Sorted L1 Norm (SLOPE). These penalties are designed to promote clustering of variables due to their sorted nature, while the nonconvexity reduces the shrinkage of coefficients. Our goal is to provide efficient ways to compute their proximal operator, enabling the use of popular proximal algorithms to solve composite optimization problems with this choice of sorted penalties. We distinguish between two classes of problems: the weakly convex case where computing the proximal operator remains a convex problem, and the nonconvex case where computing the proximal operator becomes a challenging nonconvex combinatorial problem. For the weakly convex case (e.g. sorted MCP and SCAD), we explain how the Pool Adjacent Violators (PAV) algorithm can exactly compute the proximal operator. For the nonconvex case (e.g. sorted Lq with q in ]0,1[), we show that a slight modification of this algorithm turns out to be remarkably efficient to tackle the computation of the proximal operator. We also present new theoretical insights on the minimizers of the nonconvex proximal problem. We demonstrate the practical interest of using such penalties on several experiments.

Convexity in ReLU Neural Networks: beyond ICNNs?

Convex functions and their gradients play a critical role in mathematical imaging, from proximal optimization to Optimal Transport. The successes of deep learning has led many to use learning-based methods, where fixed functions or operators are replaced by learned neural networks. Regardless of their empirical superiority, establishing rigorous guarantees for these methods often requires to impose structural constraints on neural architectures, in particular convexity. The most popular way to do so is to use so-called Input Convex Neural Networks (ICNNs). In order to explore the expressivity of ICNNs, we provide necessary and sufficient conditions for a ReLU neural network to be convex. Such characterizations are based on product of weights and activations, and write nicely for any architecture in the path-lifting framework. As particular applications, we study our characterizations in depth for 1 and 2-hidden-layer neural networks: we show that every convex function implemented by a 1-hidden-layer ReLU network can be also expressed by an ICNN with the same architecture; however this property no longer holds with more layers. Finally, we provide a numerical procedure that allows an exact check of convexity for ReLU neural networks with a large number of affine regions.

Automatic Tuning of Denoising Algorithms Parameters Without Ground Truth

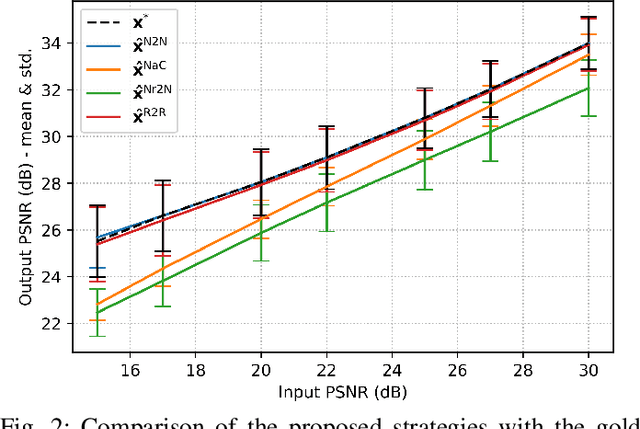
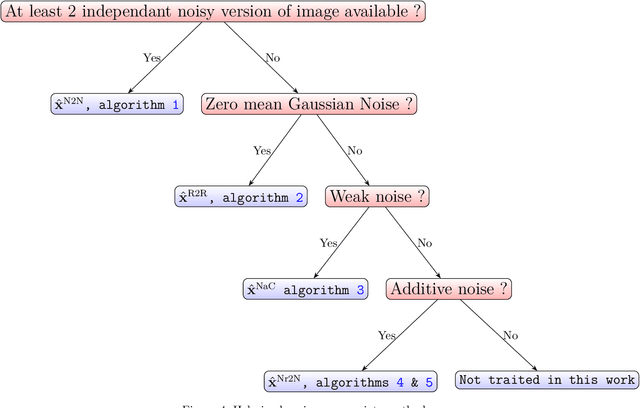
Denoising is omnipresent in image processing. It is usually addressed with algorithms relying on a set of hyperparameters that control the quality of the recovered image. Manual tuning of those parameters can be a daunting task, which calls for the development of automatic tuning methods. Given a denoising algorithm, the best set of parameters is the one that minimizes the error between denoised and ground-truth images. Clearly, this ideal approach is unrealistic, as the ground-truth images are unknown in practice. In this work, we propose unsupervised cost functions -- i.e., that only require the noisy image -- that allow us to reach this ideal gold standard performance. Specifically, the proposed approach makes it possible to obtain an average PSNR output within less than 1% of the best achievable PSNR.

Optical Diffraction Tomography Meets Fluorescence Localization Microscopy

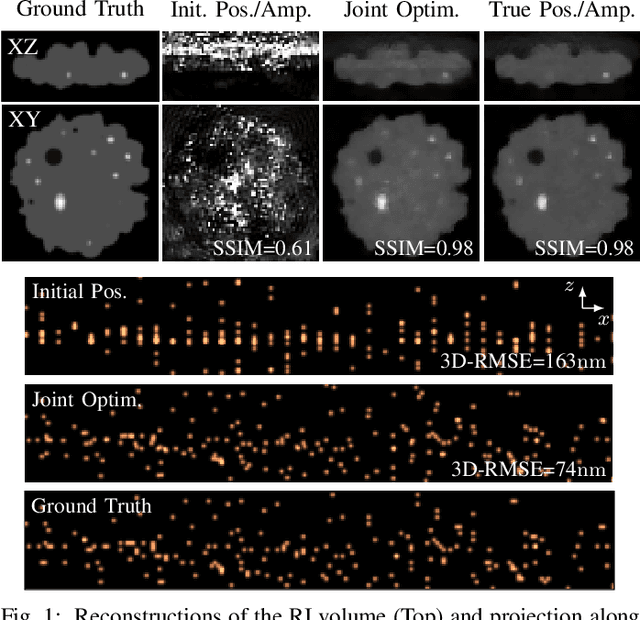
We show that structural information can be extracted from single molecule localization microscopy (SMLM) data. More precisely, we reinterpret SMLM data as the measures of a phaseless optical diffraction tomography system for which the illumination sources are fluorophores within the sample. Building upon this model, we propose a joint optimization framework to estimate both the refractive index map and the position of fluorescent molecules from the sole SMLM frames.

Deep Unrolling for Nonconvex Robust Principal Component Analysis

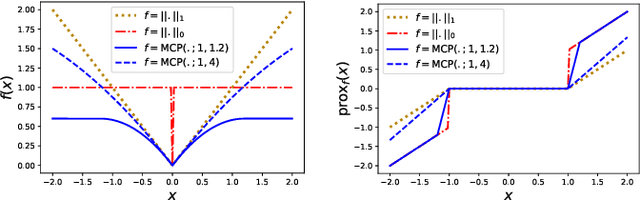
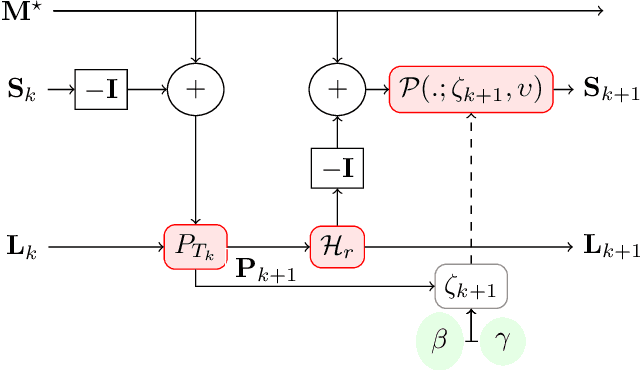
We design algorithms for Robust Principal Component Analysis (RPCA) which consists in decomposing a matrix into the sum of a low rank matrix and a sparse matrix. We propose a deep unrolled algorithm based on an accelerated alternating projection algorithm which aims to solve RPCA in its nonconvex form. The proposed procedure combines benefits of deep neural networks and the interpretability of the original algorithm and it automatically learns hyperparameters. We demonstrate the unrolled algorithm's effectiveness on synthetic datasets and also on a face modeling problem, where it leads to both better numerical and visual performances.

Accelerating Non-Negative and Bounded-Variable Linear Regression Algorithms with Safe Screening

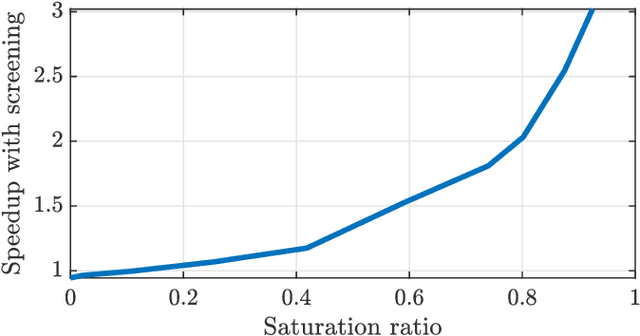
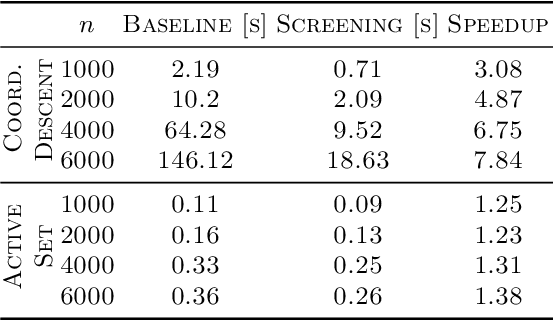
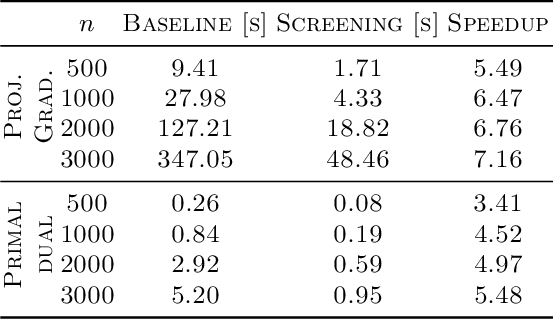
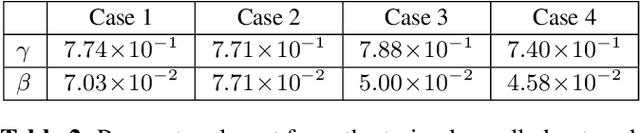
Non-negative and bounded-variable linear regression problems arise in a variety of applications in machine learning and signal processing. In this paper, we propose a technique to accelerate existing solvers for these problems by identifying saturated coordinates in the course of iterations. This is akin to safe screening techniques previously proposed for sparsity-regularized regression problems. The proposed strategy is provably safe as it provides theoretical guarantees that the identified coordinates are indeed saturated in the optimal solution. Experimental results on synthetic and real data show compelling accelerations for both non-negative and bounded-variable problems.

On the Relationships between Transform-Learning NMF and Joint-Diagonalization

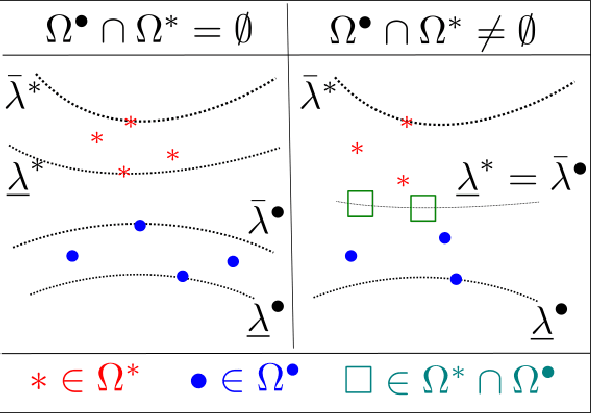
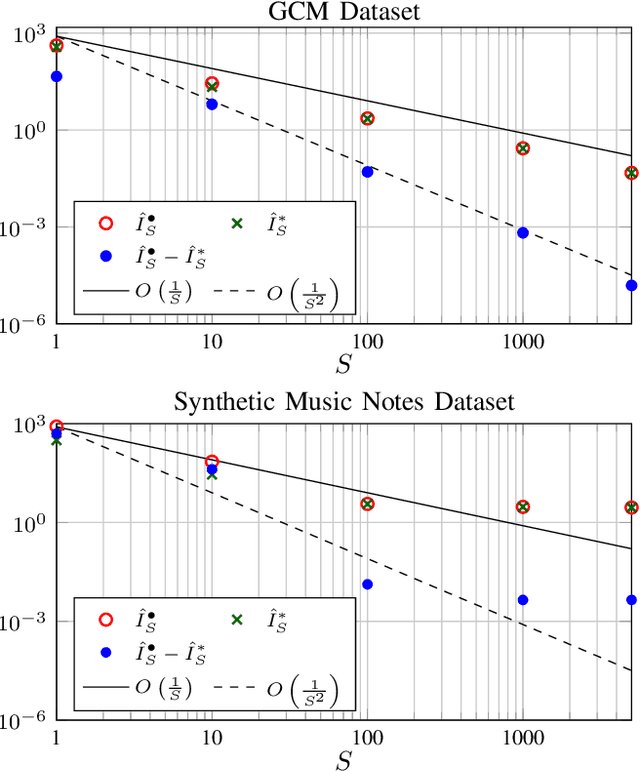
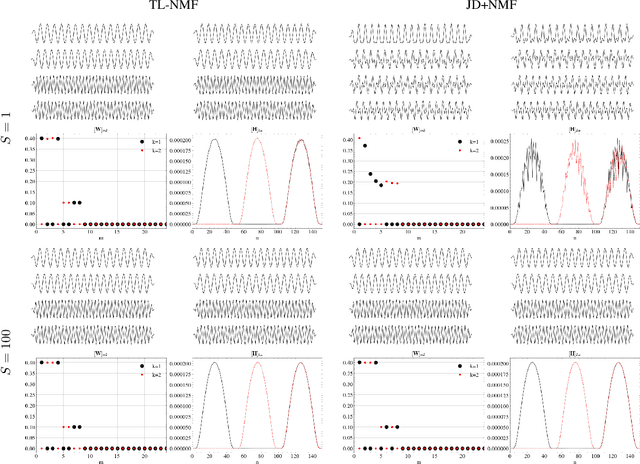
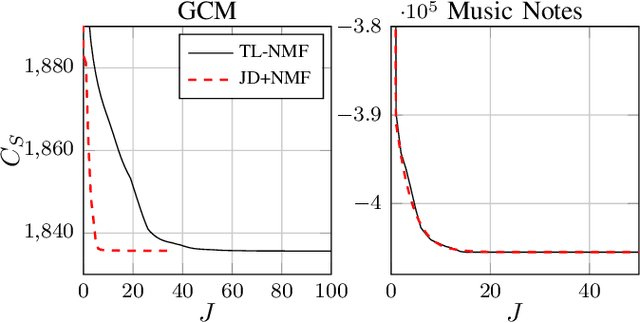
Non-negative matrix factorization with transform learning (TL-NMF) is a recent idea that aims at learning data representations suited to NMF. In this work, we relate TL-NMF to the classical matrix joint-diagonalization (JD) problem. We show that, when the number of data realizations is sufficiently large, TL-NMF can be replaced by a two-step approach -- termed as JD+NMF -- that estimates the transform through JD, prior to NMF computation. In contrast, we found that when the number of data realizations is limited, not only is JD+NMF no longer equivalent to TL-NMF, but the inherent low-rank constraint of TL-NMF turns out to be an essential ingredient to learn meaningful transforms for NMF.

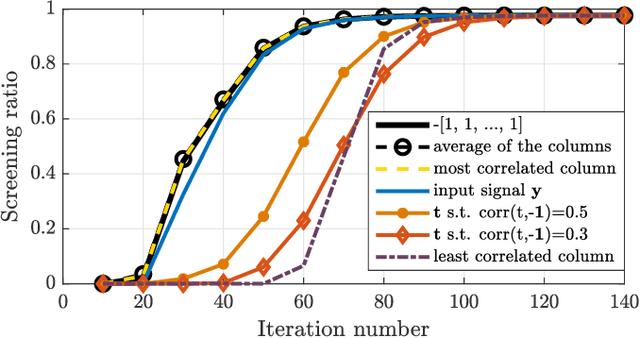
Expanding boundaries of Gap Safe screening

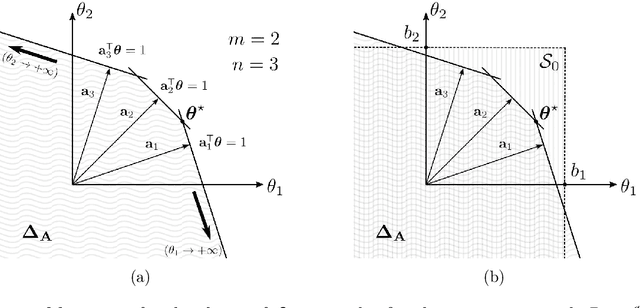
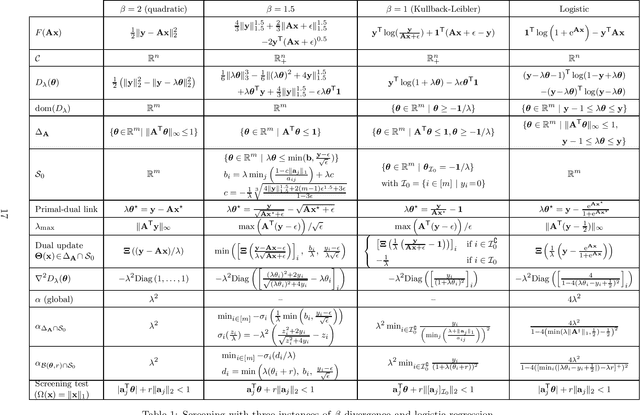
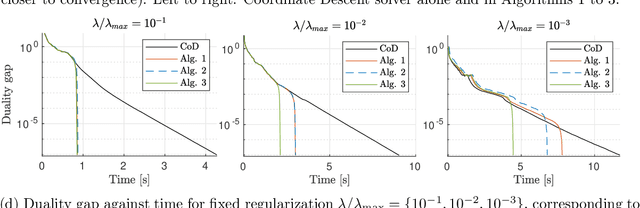
Sparse optimization problems are ubiquitous in many fields such as statistics, signal/image processing and machine learning. This has led to the birth of many iterative algorithms to solve them. A powerful strategy to boost the performance of these algorithms is known as safe screening: it allows the early identification of zero coordinates in the solution, which can then be eliminated to reduce the problem's size and accelerate convergence. In this work, we extend the existing Gap Safe screening framework by relaxing the global strong-concavity assumption on the dual cost function. Instead, we exploit local regularity properties, that is, strong concavity on well-chosen subsets of the domain. The non-negativity constraint is also integrated to the existing framework. Besides making safe screening possible to a broader class of functions that includes beta-divergences (e.g., the Kullback-Leibler divergence), the proposed approach also improves upon the existing Gap Safe screening rules on previously applicable cases (e.g., logistic regression). The proposed general framework is exemplified by some notable particular cases: logistic function, beta = 1.5 and Kullback-Leibler divergences. Finally, we showcase the effectiveness of the proposed screening rules with different solvers (coordinate descent, multiplicative-update and proximal gradient algorithms) and different data sets (binary classification, hyperspectral and count data).