Accelerating Non-Negative and Bounded-Variable Linear Regression Algorithms with Safe Screening

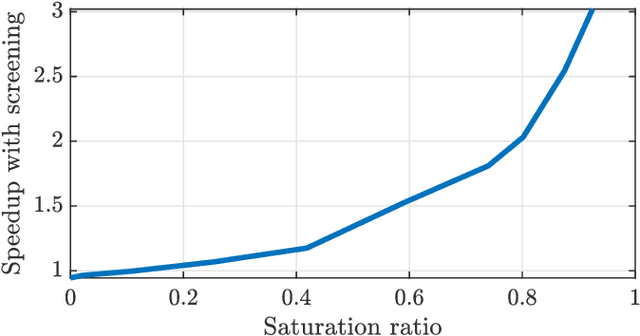
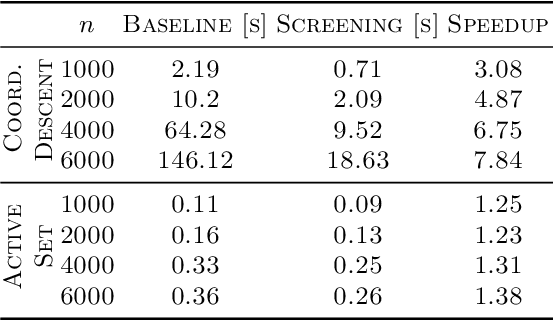
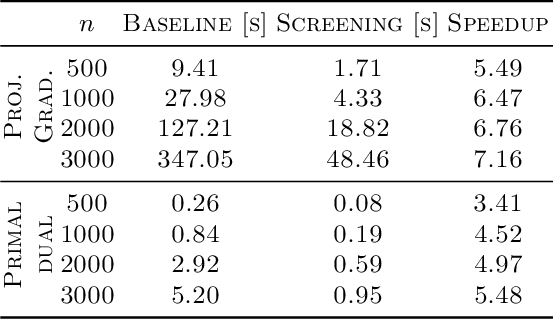
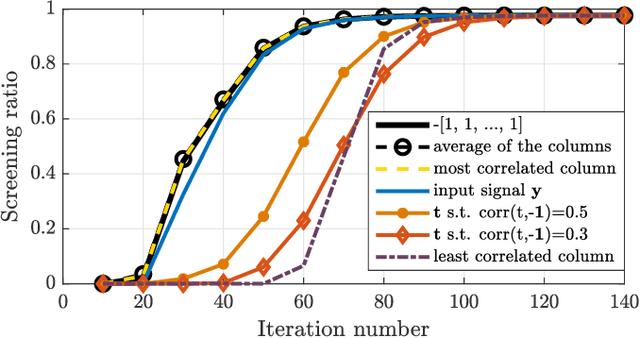
Non-negative and bounded-variable linear regression problems arise in a variety of applications in machine learning and signal processing. In this paper, we propose a technique to accelerate existing solvers for these problems by identifying saturated coordinates in the course of iterations. This is akin to safe screening techniques previously proposed for sparsity-regularized regression problems. The proposed strategy is provably safe as it provides theoretical guarantees that the identified coordinates are indeed saturated in the optimal solution. Experimental results on synthetic and real data show compelling accelerations for both non-negative and bounded-variable problems.

Expanding boundaries of Gap Safe screening

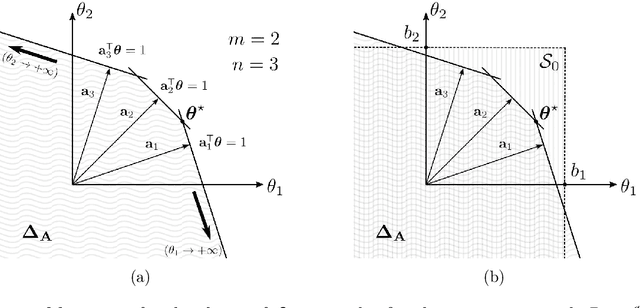
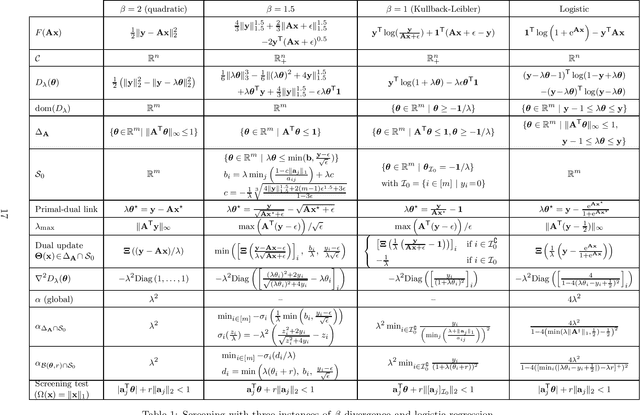
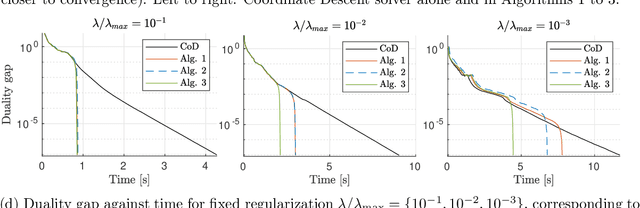
Sparse optimization problems are ubiquitous in many fields such as statistics, signal/image processing and machine learning. This has led to the birth of many iterative algorithms to solve them. A powerful strategy to boost the performance of these algorithms is known as safe screening: it allows the early identification of zero coordinates in the solution, which can then be eliminated to reduce the problem's size and accelerate convergence. In this work, we extend the existing Gap Safe screening framework by relaxing the global strong-concavity assumption on the dual cost function. Instead, we exploit local regularity properties, that is, strong concavity on well-chosen subsets of the domain. The non-negativity constraint is also integrated to the existing framework. Besides making safe screening possible to a broader class of functions that includes beta-divergences (e.g., the Kullback-Leibler divergence), the proposed approach also improves upon the existing Gap Safe screening rules on previously applicable cases (e.g., logistic regression). The proposed general framework is exemplified by some notable particular cases: logistic function, beta = 1.5 and Kullback-Leibler divergences. Finally, we showcase the effectiveness of the proposed screening rules with different solvers (coordinate descent, multiplicative-update and proximal gradient algorithms) and different data sets (binary classification, hyperspectral and count data).

Stable safe screening and structured dictionaries for faster $\ell\_{1}$ regularization

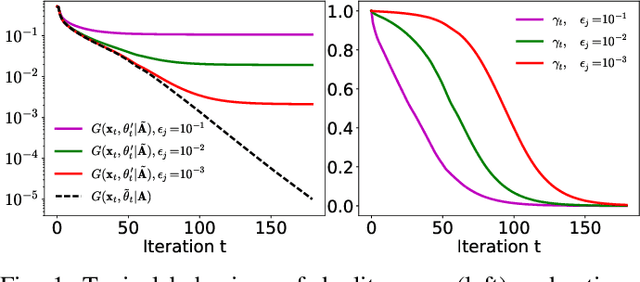
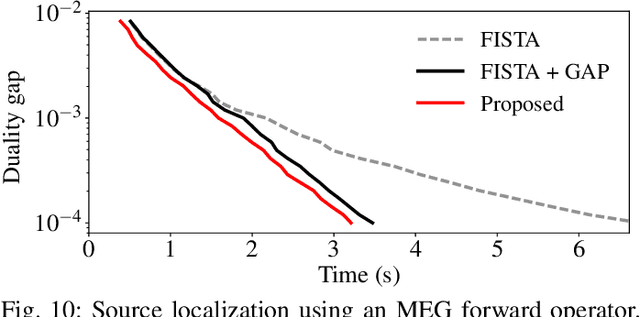
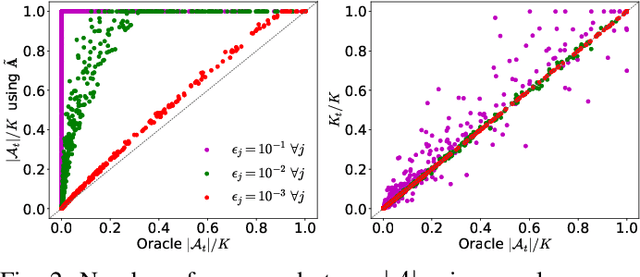
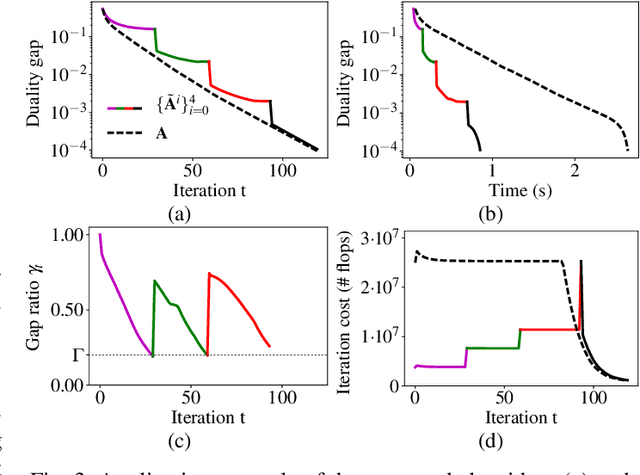
In this paper, we propose a way to combine two acceleration techniques for the $\ell_1$-regularized least squares problem: safe screening tests, which allow to eliminate useless dictionary atoms, and the use of fast structured approximations of the dictionary matrix. To do so, we introduce a new family of screening tests, termed stable screening, which can cope with approximation errors on the dictionary atoms while keeping the safety of the test (i.e. zero risk of rejecting atoms belonging to the solution support). Some of the main existing screening tests are extended to this new framework. The proposed algorithm consists in using a coarser (but faster) approximation of the dictionary at the initial iterations and then switching to better approximations until eventually adopting the original dictionary. A systematic switching criterion based on the duality gap saturation and the screening ratio is derived.Simulation results show significant reductions in both computational complexity and execution times for a wide range of tested scenarios.