Stable safe screening and structured dictionaries for faster $\ell\_{1}$ regularization

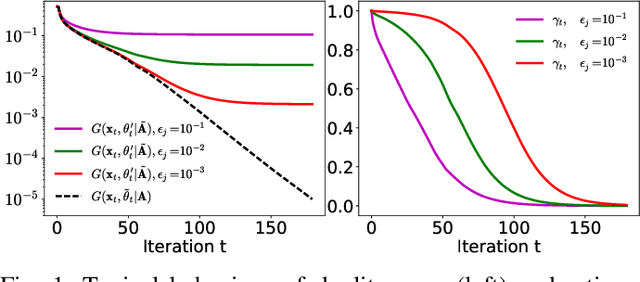
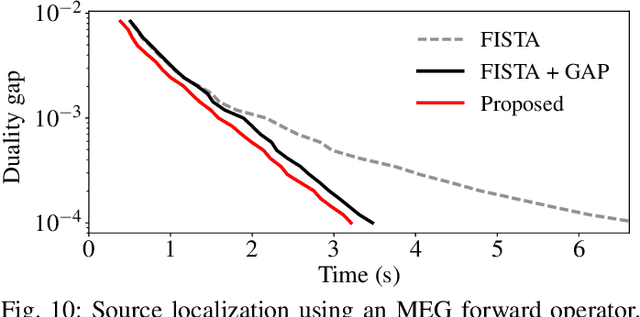
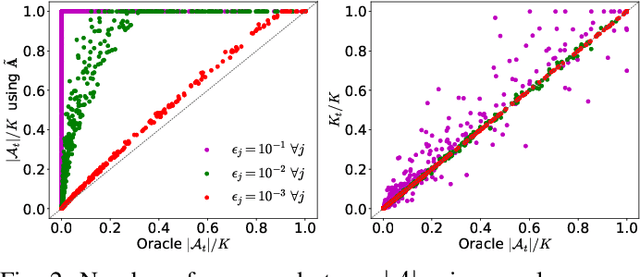
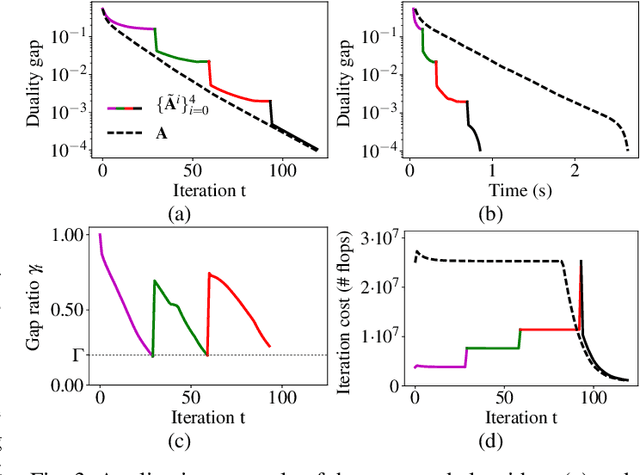
In this paper, we propose a way to combine two acceleration techniques for the $\ell_1$-regularized least squares problem: safe screening tests, which allow to eliminate useless dictionary atoms, and the use of fast structured approximations of the dictionary matrix. To do so, we introduce a new family of screening tests, termed stable screening, which can cope with approximation errors on the dictionary atoms while keeping the safety of the test (i.e. zero risk of rejecting atoms belonging to the solution support). Some of the main existing screening tests are extended to this new framework. The proposed algorithm consists in using a coarser (but faster) approximation of the dictionary at the initial iterations and then switching to better approximations until eventually adopting the original dictionary. A systematic switching criterion based on the duality gap saturation and the screening ratio is derived.Simulation results show significant reductions in both computational complexity and execution times for a wide range of tested scenarios.