Denis Kouame
Automatic Tuning of Denoising Algorithms Parameters Without Ground Truth
Jan 18, 2024Abstract:Denoising is omnipresent in image processing. It is usually addressed with algorithms relying on a set of hyperparameters that control the quality of the recovered image. Manual tuning of those parameters can be a daunting task, which calls for the development of automatic tuning methods. Given a denoising algorithm, the best set of parameters is the one that minimizes the error between denoised and ground-truth images. Clearly, this ideal approach is unrealistic, as the ground-truth images are unknown in practice. In this work, we propose unsupervised cost functions -- i.e., that only require the noisy image -- that allow us to reach this ideal gold standard performance. Specifically, the proposed approach makes it possible to obtain an average PSNR output within less than 1% of the best achievable PSNR.
Mask-guided Data Augmentation for Multiparametric MRI Generation with a Rare Hepatocellular Carcinoma
Jul 30, 2023Abstract:Data augmentation is classically used to improve the overall performance of deep learning models. It is, however, challenging in the case of medical applications, and in particular for multiparametric datasets. For example, traditional geometric transformations used in several applications to generate synthetic images can modify in a non-realistic manner the patients' anatomy. Therefore, dedicated image generation techniques are necessary in the medical field to, for example, mimic a given pathology realistically. This paper introduces a new data augmentation architecture that generates synthetic multiparametric (T1 arterial, T1 portal, and T2) magnetic resonance images (MRI) of massive macrotrabecular subtype hepatocellular carcinoma with their corresponding tumor masks through a generative deep learning approach. The proposed architecture creates liver tumor masks and abdominal edges used as input in a Pix2Pix network for synthetic data creation. The method's efficiency is demonstrated by training it on a limited multiparametric dataset of MRI triplets from $89$ patients with liver lesions to generate $1,000$ synthetic triplets and their corresponding liver tumor masks. The resulting Frechet Inception Distance score was $86.55$. The proposed approach was among the winners of the 2021 data augmentation challenge organized by the French Society of Radiology.
Joint Blind Deconvolution and Robust Principal Component Analysis for Blood Flow Estimation in Medical Ultrasound Imaging
Jul 10, 2020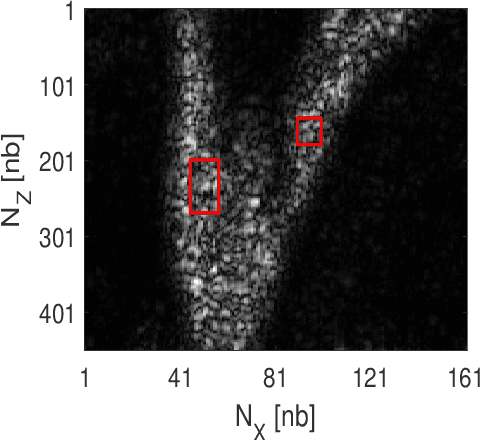
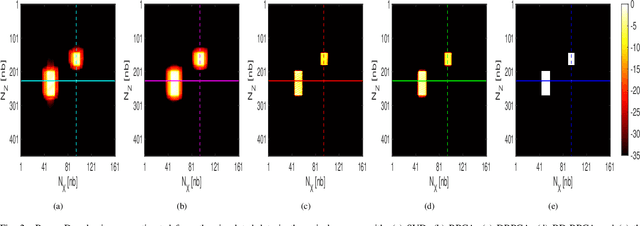
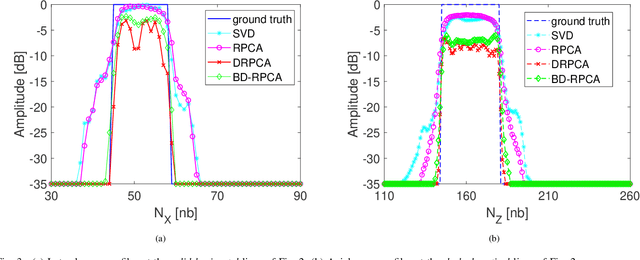
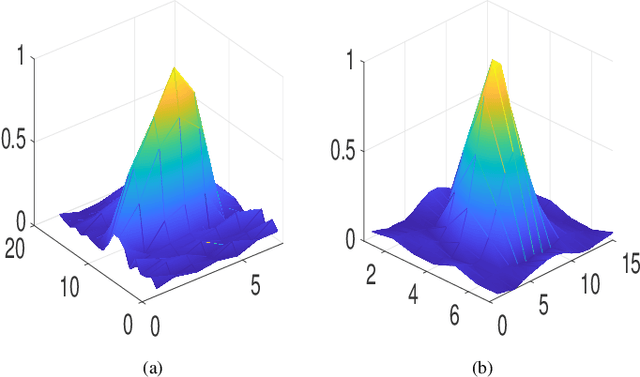
Abstract:This paper addresses the problem of high-resolution Doppler blood flow estimation from an ultrafast sequence of ultrasound images. Formulating the separation of clutter and blood components as an inverse problem has been shown in the literature to be a good alternative to spatio-temporal singular value decomposition (SVD)-based clutter filtering. In particular, a deconvolution step has recently been embedded in such a problem to mitigate the influence of the experimentally measured point spread function (PSF) of the imaging system. Deconvolution was shown in this context to improve the accuracy of the blood flow reconstruction. However, measuring the PSF requires non-trivial experimental setups. To overcome this limitation, we propose herein a blind deconvolution method able to estimate both the blood component and the PSF from Doppler data. Numerical experiments conducted on simulated and in vivo data demonstrate qualitatively and quantitatively the effectiveness of the proposed approach in comparison with the previous method based on experimentally measured PSF and two other state-of-the-art approaches.
Joint Segmentation and Deconvolution of Ultrasound Images Using a Hierarchical Bayesian Model based on Generalized Gaussian Priors
May 02, 2016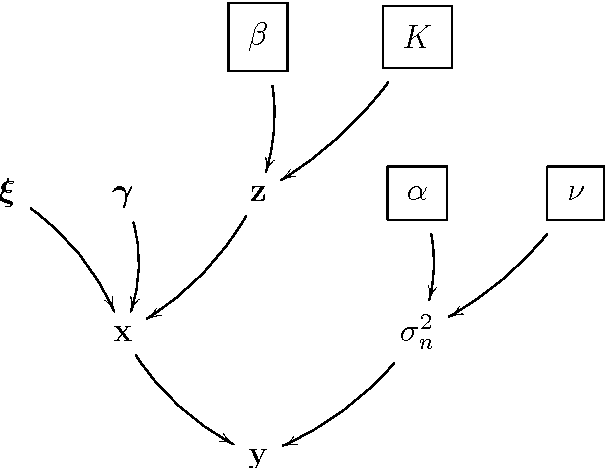
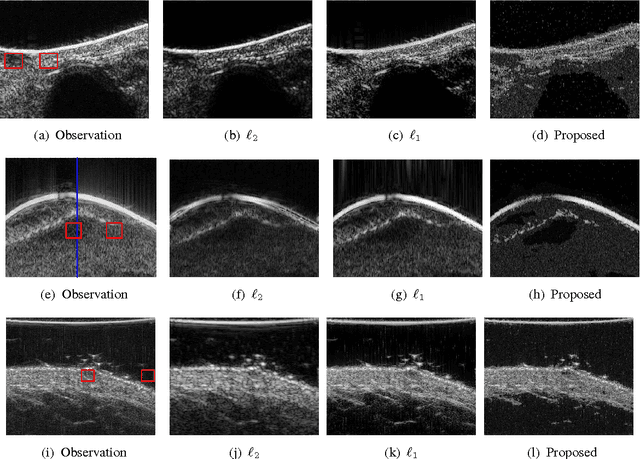
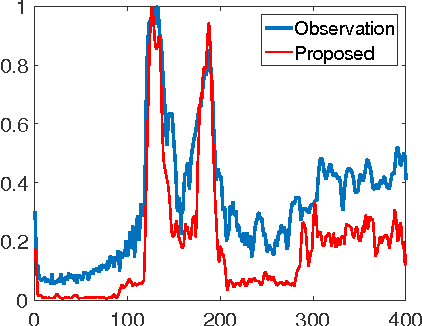
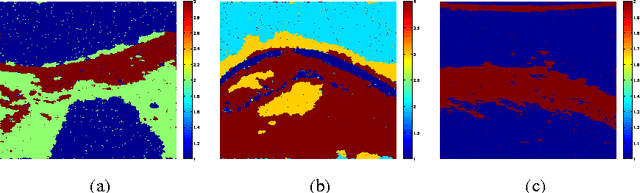
Abstract:This paper proposes a joint segmentation and deconvolution Bayesian method for medical ultrasound (US) images. Contrary to piecewise homogeneous images, US images exhibit heavy characteristic speckle patterns correlated with the tissue structures. The generalized Gaussian distribution (GGD) has been shown to be one of the most relevant distributions for characterizing the speckle in US images. Thus, we propose a GGD-Potts model defined by a label map coupling US image segmentation and deconvolution. The Bayesian estimators of the unknown model parameters, including the US image, the label map and all the hyperparameters are difficult to be expressed in closed form. Thus, we investigate a Gibbs sampler to generate samples distributed according to the posterior of interest. These generated samples are finally used to compute the Bayesian estimators of the unknown parameters. The performance of the proposed Bayesian model is compared with existing approaches via several experiments conducted on realistic synthetic data and in vivo US images.
Fast Single Image Super-Resolution
May 02, 2016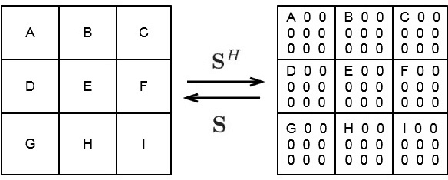


Abstract:This paper addresses the problem of single image super-resolution (SR), which consists of recovering a high resolution image from its blurred, decimated and noisy version. The existing algorithms for single image SR use different strategies to handle the decimation and blurring operators. In addition to the traditional first-order gradient methods, recent techniques investigate splitting-based methods dividing the SR problem into up-sampling and deconvolution steps that can be easily solved. Instead of following this splitting strategy, we propose to deal with the decimation and blurring operators simultaneously by taking advantage of their particular properties in the frequency domain, leading to a new fast SR approach. Specifically, an analytical solution can be obtained and implemented efficiently for the Gaussian prior or any other regularization that can be formulated into an $\ell_2$-regularized quadratic model, i.e., an $\ell_2$-$\ell_2$ optimization problem. Furthermore, the flexibility of the proposed SR scheme is shown through the use of various priors/regularizations, ranging from generic image priors to learning-based approaches. In the case of non-Gaussian priors, we show how the analytical solution derived from the Gaussian case can be embedded intotraditional splitting frameworks, allowing the computation cost of existing algorithms to be decreased significantly. Simulation results conducted on several images with different priors illustrate the effectiveness of our fast SR approach compared with the existing techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge