Duong Hung Pham
Automatic Tuning of Denoising Algorithms Parameters Without Ground Truth
Jan 18, 2024
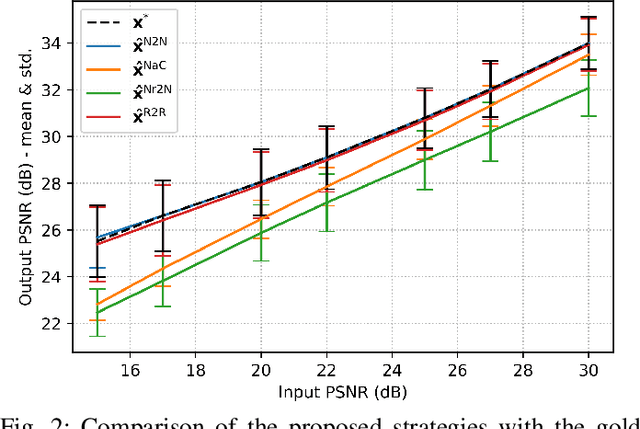

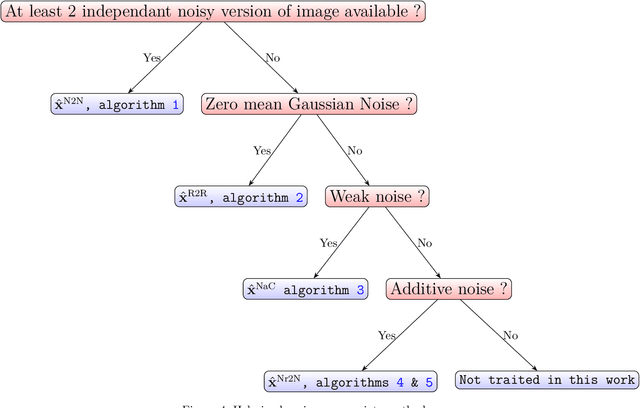
Abstract:Denoising is omnipresent in image processing. It is usually addressed with algorithms relying on a set of hyperparameters that control the quality of the recovered image. Manual tuning of those parameters can be a daunting task, which calls for the development of automatic tuning methods. Given a denoising algorithm, the best set of parameters is the one that minimizes the error between denoised and ground-truth images. Clearly, this ideal approach is unrealistic, as the ground-truth images are unknown in practice. In this work, we propose unsupervised cost functions -- i.e., that only require the noisy image -- that allow us to reach this ideal gold standard performance. Specifically, the proposed approach makes it possible to obtain an average PSNR output within less than 1% of the best achievable PSNR.
A Novel Fast 3D Single Image Super-Resolution Algorithm
Oct 29, 2020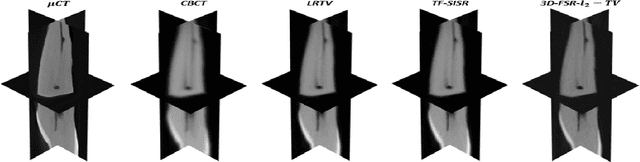
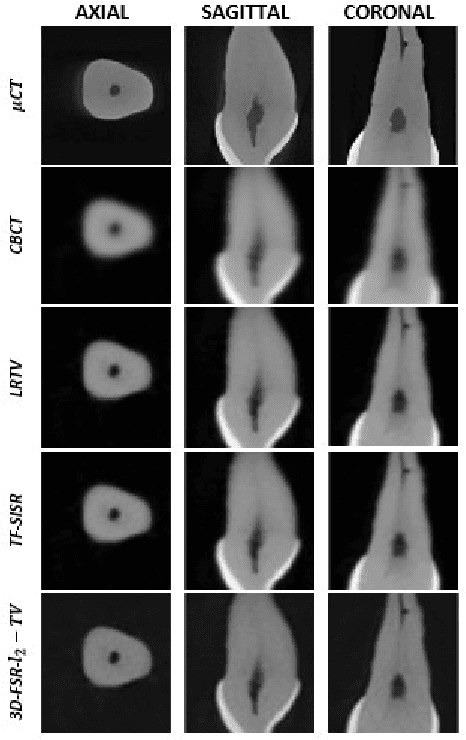


Abstract:This paper introduces a novel computationally efficient method of solving the 3D single image super-resolution (SR) problem, i.e., reconstruction of a high-resolution volume from its low-resolution counterpart. The main contribution lies in the original way of handling simultaneously the associated decimation and blurring operators, based on their underlying properties in the frequency domain. In particular, the proposed decomposition technique of the 3D decimation operator allows a straightforward implementation for Tikhonov regularization, and can be further used to take into consideration other regularization functions such as the total variation, enabling the computational cost of state-of-the-art algorithms to be considerably decreased. Numerical experiments carried out showed that the proposed approach outperforms existing 3D SR methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge