A Weighted Hankel Approach and Cramér-Rao Bound Analysis for Quantitative Acoustic Microscopy Imaging

Quantitative acoustic microscopy (QAM) is a cutting-edge imaging modality that leverages very high-frequency ultrasound to characterize the acoustic and mechanical properties of biological tissues at microscopic resolutions. Radio-frequency echo signals are digitized and processed to yield two-dimensional maps. This paper introduces a weighted Hankel-based spectral method with a reweighting strategy to enhance robustness with regard to noise and reduce unreliable acoustic parameter estimates. Additionally, we derive, for the first time in QAM, Cram\'er-Rao bounds to establish theoretical performance benchmarks for acoustic parameter estimation. Simulations and experimental results demonstrate that the proposed method consistently outperform standard autoregressive approach, particularly under challenging conditions. These advancements promise to improve the accuracy and reliability of tissue characterization, enhancing the potential of QAM for biomedical applications.

Quantum Algorithm for Signal Denoising

This letter presents a novel \textit{quantum algorithm} for signal denoising, which performs a thresholding in the frequency domain through amplitude amplification and using an adaptive threshold determined by local mean values. The proposed algorithm is able to process \textit{both classical and quantum} signals. It is parametrically faster than previous classical and quantum denoising algorithms. Numerical results show that it is efficient at removing noise of both classical and quantum origin, significantly outperforming existing quantum algorithms in this respect, especially in the presence of quantum noise.

DIVA: Deep Unfolded Network from Quantum Interactive Patches for Image Restoration

This paper presents a deep neural network called DIVA unfolding a baseline adaptive denoising algorithm (De-QuIP), relying on the theory of quantum many-body physics. Furthermore, it is shown that with very slight modifications, this network can be enhanced to solve more challenging image restoration tasks such as image deblurring, super-resolution and inpainting. Despite a compact and interpretable (from a physical perspective) architecture, the proposed deep learning network outperforms several recent algorithms from the literature, designed specifically for each task. The key ingredients of the proposed method are on one hand, its ability to handle non-local image structures through the patch-interaction term and the quantum-based Hamiltonian operator, and, on the other hand, its flexibility to adapt the hyperparameters patch-wisely, due to the training process.

A Novel Image Denoising Algorithm Using Concepts of Quantum Many-Body Theory

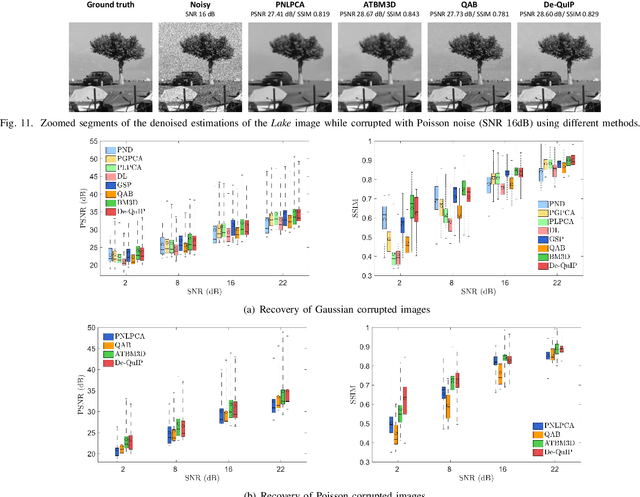
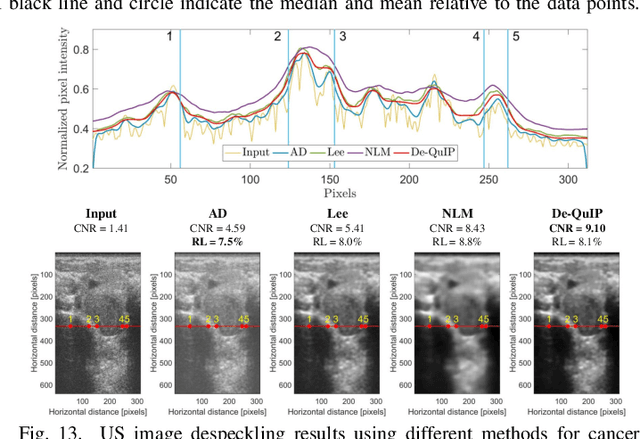
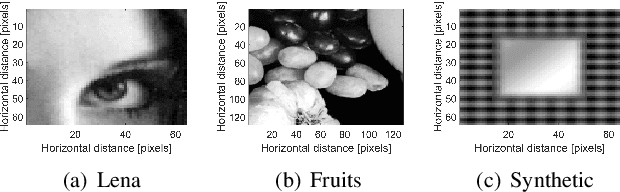
Sparse representation of real-life images is a very effective approach in imaging applications, such as denoising. In recent years, with the growth of computing power, data-driven strategies exploiting the redundancy within patches extracted from one or several images to increase sparsity have become more prominent. This paper presents a novel image denoising algorithm exploiting such an image-dependent basis inspired by the quantum many-body theory. Based on patch analysis, the similarity measures in a local image neighborhood are formalized through a term akin to interaction in quantum mechanics that can efficiently preserve the local structures of real images. The versatile nature of this adaptive basis extends the scope of its application to image-independent or image-dependent noise scenarios without any adjustment. We carry out a rigorous comparison with contemporary methods to demonstrate the denoising capability of the proposed algorithm regardless of the image characteristics, noise statistics and intensity. We illustrate the properties of the hyperparameters and their respective effects on the denoising performance, together with automated rules of selecting their values close to the optimal one in experimental setups with ground truth not available. Finally, we show the ability of our approach to deal with practical images denoising problems such as medical ultrasound image despeckling applications.

Reconstruction of Sentinel-2 Time Series Using Robust Gaussian Mixture Models -- Application to the Detection of Anomalous Crop Development in wheat and rapeseed crops

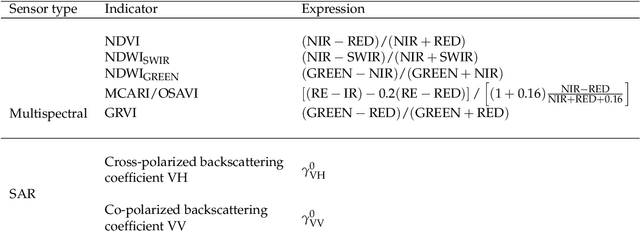
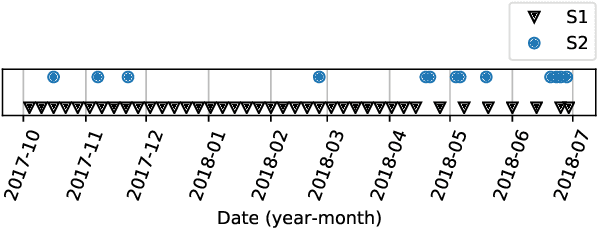
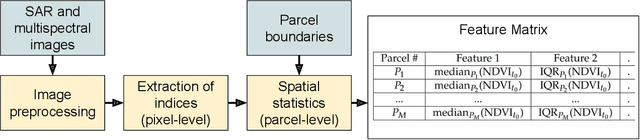
Missing data is a recurrent problem in remote sensing, mainly due to cloud coverage for multispectral images and acquisition problems. This can be a critical issue for crop monitoring, especially for applications relying on machine learning techniques, which generally assume that the feature matrix does not have missing values. This paper proposes a Gaussian Mixture Model (GMM) for the reconstruction of parcel-level features extracted from multispectral images. A robust version of the GMM is also investigated, since datasets can be contaminated by inaccurate samples or features (e.g., wrong crop type reported, inaccurate boundaries, undetected clouds, etc). Additional features extracted from Synthetic Aperture Radar (SAR) images using Sentinel-1 data are also used to provide complementary information and improve the imputations. The robust GMM investigated in this work assigns reduced weights to the outliers during the estimation of the GMM parameters, which improves the final reconstruction. These weights are computed at each step of an Expectation-Maximization (EM) algorithm by using outlier scores provided by the isolation forest algorithm. Experimental validation is conducted on rapeseed and wheat parcels located in the Beauce region (France). Overall, we show that the GMM imputation method outperforms other reconstruction strategies. A mean absolute error (MAE) of 0.013 (resp. 0.019) is obtained for the imputation of the median Normalized Difference Index (NDVI) of the rapeseed (resp. wheat) parcels. Other indicators (e.g., Normalized Difference Water Index) and statistics (for instance the interquartile range, which captures heterogeneity among the parcel indicator) are reconstructed at the same time with good accuracy. In a dataset contaminated by irrelevant samples, using the robust GMM is recommended since the standard GMM imputation can lead to inaccurate imputed values.

Image Denoising Inspired by Quantum Many-Body physics

Decomposing an image through Fourier, DCT or wavelet transforms is still a common approach in digital image processing, in number of applications such as denoising. In this context, data-driven dictionaries and in particular exploiting the redundancy withing patches extracted from one or several images allowed important improvements. This paper proposes an original idea of constructing such an image-dependent basis inspired by the principles of quantum many-body physics. The similarity between two image patches is introduced in the formalism through a term akin to interaction terms in quantum mechanics. The main contribution of the paper is thus to introduce this original way of exploiting quantum many-body ideas in image processing, which opens interesting perspectives in image denoising. The potential of the proposed adaptive decomposition is illustrated through image denoising in presence of additive white Gaussian noise, but the method can be used for other types of noise such as image-dependent noise as well. Finally, the results show that our method achieves comparable or slightly better results than existing approaches.

Plug-and-Play Quantum Adaptive Denoiser for Deconvolving Poisson Noisy Images

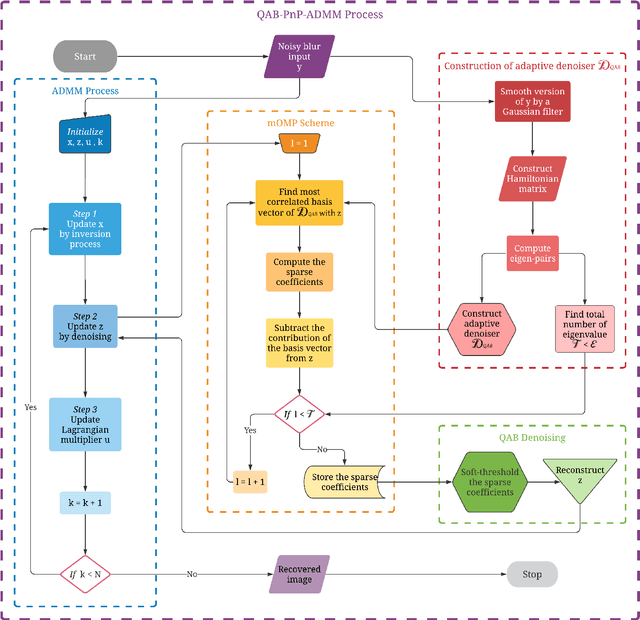
A new Plug-and-Play (PnP) alternating direction of multipliers (ADMM) scheme is proposed in this paper, by embedding a recently introduced adaptive denoiser using the Schroedinger equation's solutions of quantum physics. The potential of the proposed model is studied for Poisson image deconvolution, which is a common problem occurring in number of imaging applications, such as, for example, limited photon acquisition or X-ray computed tomography. Numerical results show the efficiency and good adaptability of the proposed scheme compared to recent state-of-the-art techniques, for both high and low signal-to-noise ratio scenarios. This performance gain regardless of the amount of noise affecting the observations is explained by the flexibility of the embedded quantum denoiser constructed without anticipating any prior statistics about the noise, which is one of the main advantages of this method.

A Novel Fast 3D Single Image Super-Resolution Algorithm

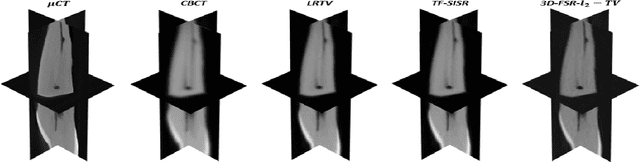
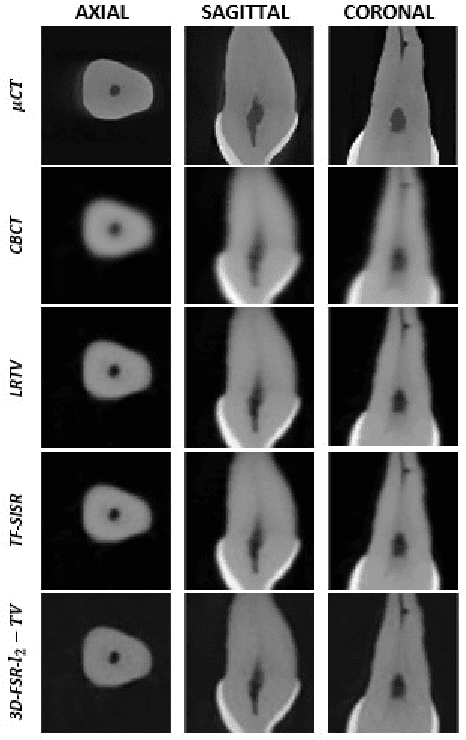
This paper introduces a novel computationally efficient method of solving the 3D single image super-resolution (SR) problem, i.e., reconstruction of a high-resolution volume from its low-resolution counterpart. The main contribution lies in the original way of handling simultaneously the associated decimation and blurring operators, based on their underlying properties in the frequency domain. In particular, the proposed decomposition technique of the 3D decimation operator allows a straightforward implementation for Tikhonov regularization, and can be further used to take into consideration other regularization functions such as the total variation, enabling the computational cost of state-of-the-art algorithms to be considerably decreased. Numerical experiments carried out showed that the proposed approach outperforms existing 3D SR methods.

Unsupervised crop anomaly detection at the parcel-level using optical and SAR images: application to wheat and rapeseed crops

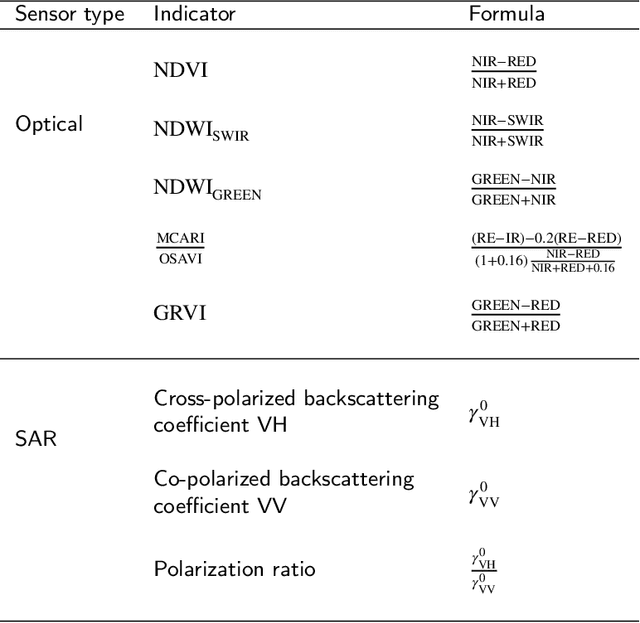
This paper proposes a generic approach for crop anomaly detection at the parcel-level based on unsupervised point anomaly detection techniques. The input data is derived from synthetic aperture radar (SAR) and optical images acquired using Sentinel-1 and Sentinel-2 satellites. The proposed strategy consists of four sequential steps: acquisition and preprocessing of optical and SAR images, extraction of optical and SAR indicators, computation of zonal statistics at the parcel-level and point anomaly detection. This paper analyzes different factors that can affect the results of anomaly detection such as the considered features and the anomaly detection algorithm used. The proposed procedure is validated on two crop types in Beauce (France), namely, rapeseed and wheat crops. Two different parcel delineation databases are considered to validate the robustness of the strategy to changes in parcel boundaries.

A Tensor Factorization Method for 3D Super-Resolution with Application to Dental CT

Available super-resolution techniques for 3D images are either computationally inefficient prior-knowledge-based iterative techniques or deep learning methods which require a large database of known low- and high-resolution image pairs. A recently introduced tensor-factorization-based approach offers a fast solution without the use of known image pairs or strict prior assumptions. In this article this factorization framework is investigated for single image resolution enhancement with an off-line estimate of the system point spread function. The technique is applied to 3D cone beam computed tomography for dental image resolution enhancement. To demonstrate the efficiency of our method, it is compared to a recent state-of-the-art iterative technique using low-rank and total variation regularizations. In contrast to this comparative technique, the proposed reconstruction technique gives a 2-order-of-magnitude improvement in running time -- 2 minutes compared to 2 hours for a dental volume of 282$\times$266$\times$392 voxels. Furthermore, it also offers slightly improved quantitative results (peak signal-to-noise ratio, segmentation quality). Another advantage of the presented technique is the low number of hyperparameters. As demonstrated in this paper, the framework is not sensitive to small changes of its parameters, proposing an ease of use.