Quantum Algorithm for Signal Denoising

This letter presents a novel \textit{quantum algorithm} for signal denoising, which performs a thresholding in the frequency domain through amplitude amplification and using an adaptive threshold determined by local mean values. The proposed algorithm is able to process \textit{both classical and quantum} signals. It is parametrically faster than previous classical and quantum denoising algorithms. Numerical results show that it is efficient at removing noise of both classical and quantum origin, significantly outperforming existing quantum algorithms in this respect, especially in the presence of quantum noise.

DIVA: Deep Unfolded Network from Quantum Interactive Patches for Image Restoration

This paper presents a deep neural network called DIVA unfolding a baseline adaptive denoising algorithm (De-QuIP), relying on the theory of quantum many-body physics. Furthermore, it is shown that with very slight modifications, this network can be enhanced to solve more challenging image restoration tasks such as image deblurring, super-resolution and inpainting. Despite a compact and interpretable (from a physical perspective) architecture, the proposed deep learning network outperforms several recent algorithms from the literature, designed specifically for each task. The key ingredients of the proposed method are on one hand, its ability to handle non-local image structures through the patch-interaction term and the quantum-based Hamiltonian operator, and, on the other hand, its flexibility to adapt the hyperparameters patch-wisely, due to the training process.

A Novel Image Denoising Algorithm Using Concepts of Quantum Many-Body Theory

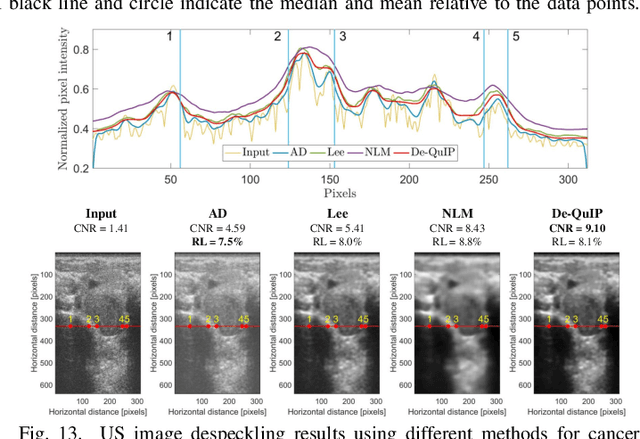
Sparse representation of real-life images is a very effective approach in imaging applications, such as denoising. In recent years, with the growth of computing power, data-driven strategies exploiting the redundancy within patches extracted from one or several images to increase sparsity have become more prominent. This paper presents a novel image denoising algorithm exploiting such an image-dependent basis inspired by the quantum many-body theory. Based on patch analysis, the similarity measures in a local image neighborhood are formalized through a term akin to interaction in quantum mechanics that can efficiently preserve the local structures of real images. The versatile nature of this adaptive basis extends the scope of its application to image-independent or image-dependent noise scenarios without any adjustment. We carry out a rigorous comparison with contemporary methods to demonstrate the denoising capability of the proposed algorithm regardless of the image characteristics, noise statistics and intensity. We illustrate the properties of the hyperparameters and their respective effects on the denoising performance, together with automated rules of selecting their values close to the optimal one in experimental setups with ground truth not available. Finally, we show the ability of our approach to deal with practical images denoising problems such as medical ultrasound image despeckling applications.

Image Denoising Inspired by Quantum Many-Body physics

Decomposing an image through Fourier, DCT or wavelet transforms is still a common approach in digital image processing, in number of applications such as denoising. In this context, data-driven dictionaries and in particular exploiting the redundancy withing patches extracted from one or several images allowed important improvements. This paper proposes an original idea of constructing such an image-dependent basis inspired by the principles of quantum many-body physics. The similarity between two image patches is introduced in the formalism through a term akin to interaction terms in quantum mechanics. The main contribution of the paper is thus to introduce this original way of exploiting quantum many-body ideas in image processing, which opens interesting perspectives in image denoising. The potential of the proposed adaptive decomposition is illustrated through image denoising in presence of additive white Gaussian noise, but the method can be used for other types of noise such as image-dependent noise as well. Finally, the results show that our method achieves comparable or slightly better results than existing approaches.

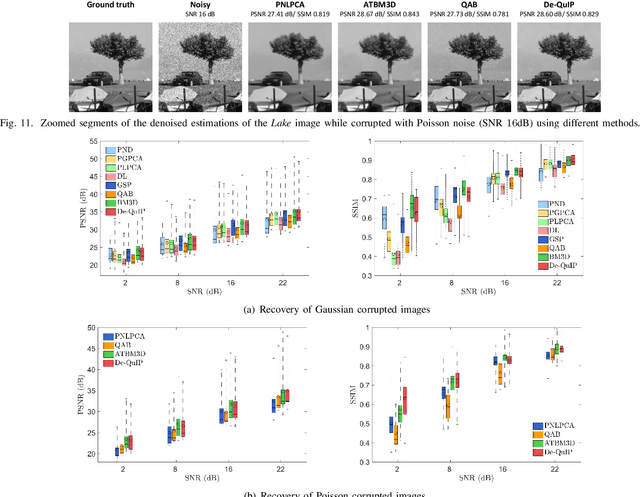
Plug-and-Play Quantum Adaptive Denoiser for Deconvolving Poisson Noisy Images

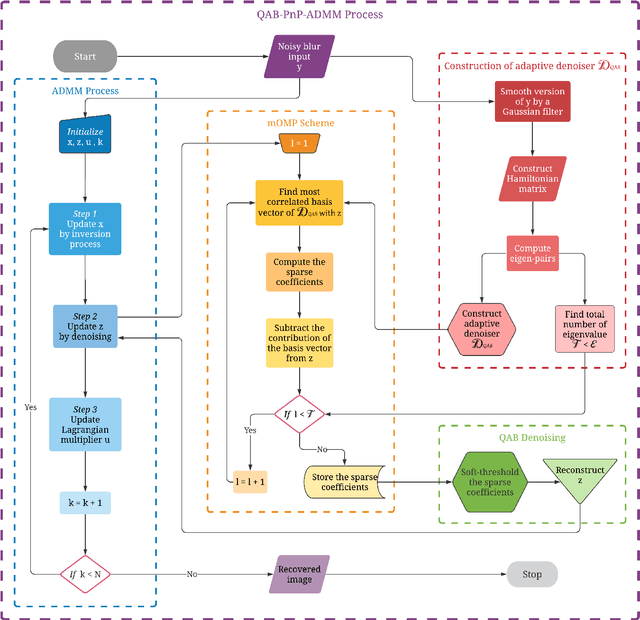
A new Plug-and-Play (PnP) alternating direction of multipliers (ADMM) scheme is proposed in this paper, by embedding a recently introduced adaptive denoiser using the Schroedinger equation's solutions of quantum physics. The potential of the proposed model is studied for Poisson image deconvolution, which is a common problem occurring in number of imaging applications, such as, for example, limited photon acquisition or X-ray computed tomography. Numerical results show the efficiency and good adaptability of the proposed scheme compared to recent state-of-the-art techniques, for both high and low signal-to-noise ratio scenarios. This performance gain regardless of the amount of noise affecting the observations is explained by the flexibility of the embedded quantum denoiser constructed without anticipating any prior statistics about the noise, which is one of the main advantages of this method.