Quantized Approximately Orthogonal Recurrent Neural Networks

Orthogonal recurrent neural networks (ORNNs) are an appealing option for learning tasks involving time series with long-term dependencies, thanks to their simplicity and computational stability. However, these networks often require a substantial number of parameters to perform well, which can be prohibitive in power-constrained environments, such as compact devices. One approach to address this issue is neural network quantization. The construction of such networks remains an open problem, acknowledged for its inherent instability.In this paper, we explore the quantization of the recurrent and input weight matrices in ORNNs, leading to Quantized approximately Orthogonal RNNs (QORNNs). We investigate one post-training quantization (PTQ) strategy and three quantization-aware training (QAT) algorithms that incorporate orthogonal constraints and quantized weights. Empirical results demonstrate the advantages of employing QAT over PTQ. The most efficient model achieves results similar to state-of-the-art full-precision ORNN and LSTM on a variety of standard benchmarks, even with 3-bits quantization.

A general approximation lower bound in $L^p$ norm, with applications to feed-forward neural networks

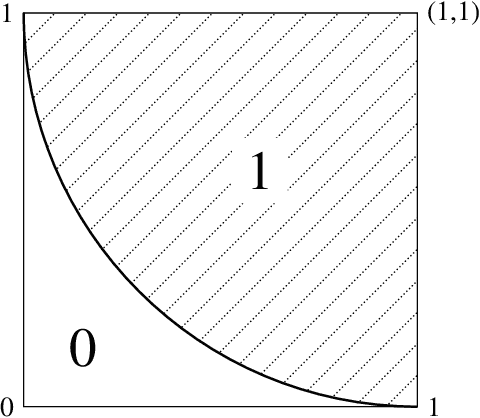
We study the fundamental limits to the expressive power of neural networks. Given two sets $F$, $G$ of real-valued functions, we first prove a general lower bound on how well functions in $F$ can be approximated in $L^p(\mu)$ norm by functions in $G$, for any $p \geq 1$ and any probability measure $\mu$. The lower bound depends on the packing number of $F$, the range of $F$, and the fat-shattering dimension of $G$. We then instantiate this bound to the case where $G$ corresponds to a piecewise-polynomial feed-forward neural network, and describe in details the application to two sets $F$: H{\"o}lder balls and multivariate monotonic functions. Beside matching (known or new) upper bounds up to log factors, our lower bounds shed some light on the similarities or differences between approximation in $L^p$ norm or in sup norm, solving an open question by DeVore et al. (2021). Our proof strategy differs from the sup norm case and uses a key probability result of Mendelson (2002).