Fair Online Bilateral Trade

In online bilateral trade, a platform posts prices to incoming pairs of buyers and sellers that have private valuations for a certain good. If the price is lower than the buyers' valuation and higher than the sellers' valuation, then a trade takes place. Previous work focused on the platform perspective, with the goal of setting prices maximizing the gain from trade (the sum of sellers' and buyers' utilities). Gain from trade is, however, potentially unfair to traders, as they may receive highly uneven shares of the total utility. In this work we enforce fairness by rewarding the platform with the fair gain from trade, defined as the minimum between sellers' and buyers' utilities. After showing that any no-regret learning algorithm designed to maximize the sum of the utilities may fail badly with fair gain from trade, we present our main contribution: a complete characterization of the regret regimes for fair gain from trade when, after each interaction, the platform only learns whether each trader accepted the current price. Specifically, we prove the following regret bounds: $\Theta(\ln T)$ in the deterministic setting, $\Omega(T)$ in the stochastic setting, and $\tilde{\Theta}(T^{2/3})$ in the stochastic setting when sellers' and buyers' valuations are independent of each other. We conclude by providing tight regret bounds when, after each interaction, the platform is allowed to observe the true traders' valuations.

Variational autoencoder with weighted samples for high-dimensional non-parametric adaptive importance sampling

Probability density function estimation with weighted samples is the main foundation of all adaptive importance sampling algorithms. Classically, a target distribution is approximated either by a non-parametric model or within a parametric family. However, these models suffer from the curse of dimensionality or from their lack of flexibility. In this contribution, we suggest to use as the approximating model a distribution parameterised by a variational autoencoder. We extend the existing framework to the case of weighted samples by introducing a new objective function. The flexibility of the obtained family of distributions makes it as expressive as a non-parametric model, and despite the very high number of parameters to estimate, this family is much more efficient in high dimension than the classical Gaussian or Gaussian mixture families. Moreover, in order to add flexibility to the model and to be able to learn multimodal distributions, we consider a learnable prior distribution for the variational autoencoder latent variables. We also introduce a new pre-training procedure for the variational autoencoder to find good starting weights of the neural networks to prevent as much as possible the posterior collapse phenomenon to happen. At last, we explicit how the resulting distribution can be combined with importance sampling, and we exploit the proposed procedure in existing adaptive importance sampling algorithms to draw points from a target distribution and to estimate a rare event probability in high dimension on two multimodal problems.

Improved learning theory for kernel distribution regression with two-stage sampling

The distribution regression problem encompasses many important statistics and machine learning tasks, and arises in a large range of applications. Among various existing approaches to tackle this problem, kernel methods have become a method of choice. Indeed, kernel distribution regression is both computationally favorable, and supported by a recent learning theory. This theory also tackles the two-stage sampling setting, where only samples from the input distributions are available. In this paper, we improve the learning theory of kernel distribution regression. We address kernels based on Hilbertian embeddings, that encompass most, if not all, of the existing approaches. We introduce the novel near-unbiased condition on the Hilbertian embeddings, that enables us to provide new error bounds on the effect of the two-stage sampling, thanks to a new analysis. We show that this near-unbiased condition holds for three important classes of kernels, based on optimal transport and mean embedding. As a consequence, we strictly improve the existing convergence rates for these kernels. Our setting and results are illustrated by numerical experiments.

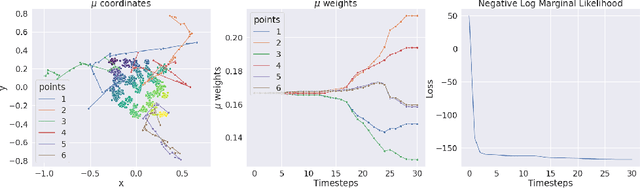
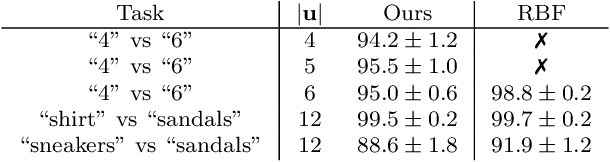
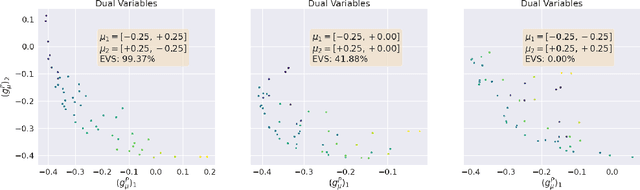
Gaussian Processes on Distributions based on Regularized Optimal Transport

We present a novel kernel over the space of probability measures based on the dual formulation of optimal regularized transport. We propose an Hilbertian embedding of the space of probabilities using their Sinkhorn potentials, which are solutions of the dual entropic relaxed optimal transport between the probabilities and a reference measure $\mathcal{U}$. We prove that this construction enables to obtain a valid kernel, by using the Hilbert norms. We prove that the kernel enjoys theoretical properties such as universality and some invariances, while still being computationally feasible. Moreover we provide theoretical guarantees on the behaviour of a Gaussian process based on this kernel. The empirical performances are compared with other traditional choices of kernels for processes indexed on distributions.

Large-Sample Properties of Non-Stationary Source Separation for Gaussian Signals

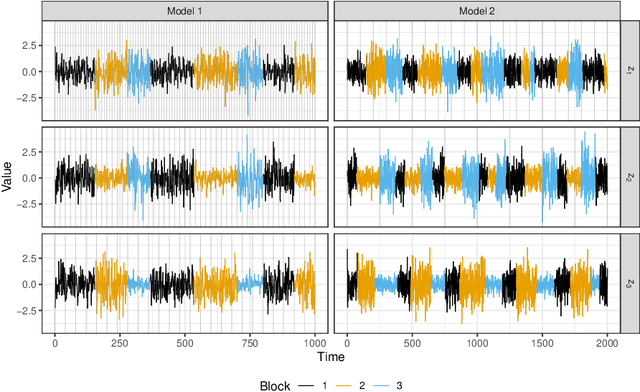
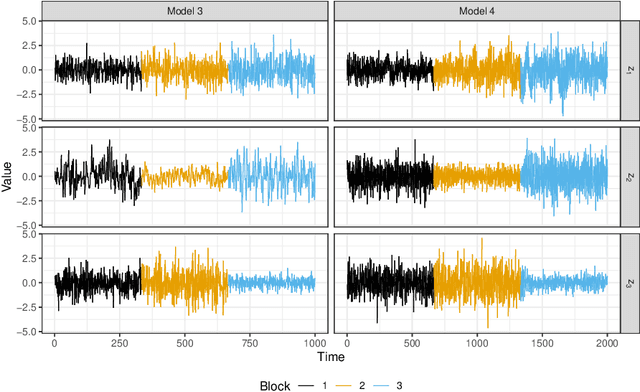
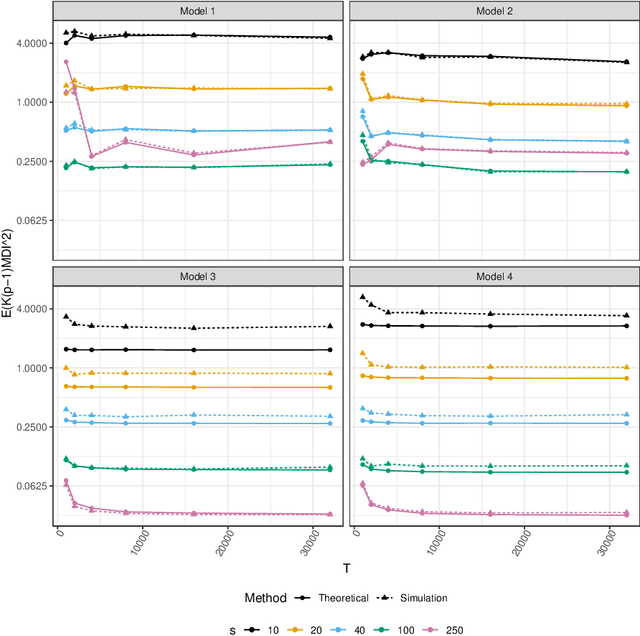
Non-stationary source separation is a well-established branch of blind source separation with many different methods. However, for none of these methods large-sample results are available. To bridge this gap, we develop large-sample theory for NSS-JD, a popular method of non-stationary source separation based on the joint diagonalization of block-wise covariance matrices. We work under an instantaneous linear mixing model for independent Gaussian non-stationary source signals together with a very general set of assumptions: besides boundedness conditions, the only assumptions we make are that the sources exhibit finite dependency and that their variance functions differ sufficiently to be asymptotically separable. The consistency of the unmixing estimator and its convergence to a limiting Gaussian distribution at the standard square root rate are shown to hold under the previous conditions. Simulation experiments are used to verify the theoretical results and to study the impact of block length on the separation.

Regret Analysis of Dyadic Search

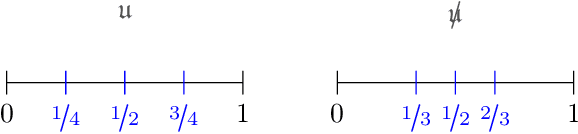
We analyze the cumulative regret of the Dyadic Search algorithm of Bachoc et al. [2022].

A Near-Optimal Algorithm for Univariate Zeroth-Order Budget Convex Optimization

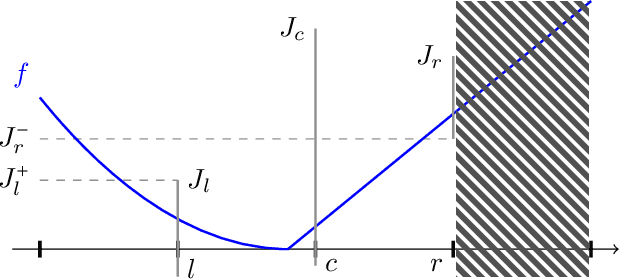
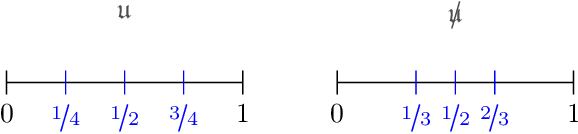
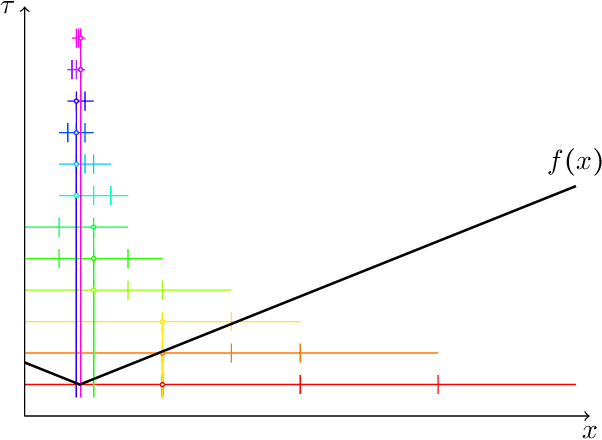
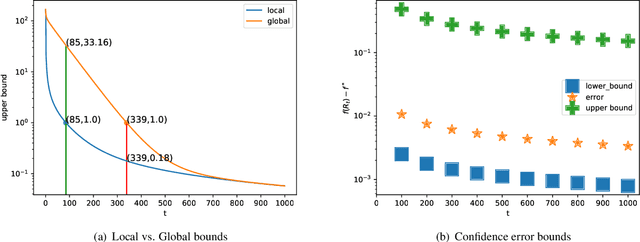
This paper studies a natural generalization of the problem of minimizing a univariate convex function $f$ by querying its values sequentially. At each time-step $t$, the optimizer can invest a budget $b_t$ in a query point $X_t$ of their choice to obtain a fuzzy evaluation of $f$ at $X_t$ whose accuracy depends on the amount of budget invested in $X_t$ across times. This setting is motivated by the minimization of objectives whose values can only be determined approximately through lengthy or expensive computations. We design an any-time parameter-free algorithm called Dyadic Search, for which we prove near-optimal optimization error guarantees. As a byproduct of our analysis, we show that the classical dependence on the global Lipschitz constant in the error bounds is an artifact of the granularity of the budget. Finally, we illustrate our theoretical findings with numerical simulations.

Local Identifiability of Deep ReLU Neural Networks: the Theory

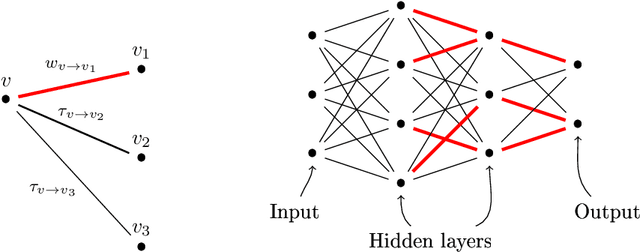
Is a sample rich enough to determine, at least locally, the parameters of a neural network? To answer this question, we introduce a new local parameterization of a given deep ReLU neural network by fixing the values of some of its weights. This allows us to define local lifting operators whose inverses are charts of a smooth manifold of a high dimensional space. The function implemented by the deep ReLU neural network composes the local lifting with a linear operator which depends on the sample. We derive from this convenient representation a geometrical necessary and sufficient condition of local identifiability. Looking at tangent spaces, the geometrical condition provides: 1/ a sharp and testable necessary condition of identifiability and 2/ a sharp and testable sufficient condition of local identifiability. The validity of the conditions can be tested numerically using backpropagation and matrix rank computations.

High-dimensional additive Gaussian processes under monotonicity constraints

We introduce an additive Gaussian process framework accounting for monotonicity constraints and scalable to high dimensions. Our contributions are threefold. First, we show that our framework enables to satisfy the constraints everywhere in the input space. We also show that more general componentwise linear inequality constraints can be handled similarly, such as componentwise convexity. Second, we propose the additive MaxMod algorithm for sequential dimension reduction. By sequentially maximizing a squared-norm criterion, MaxMod identifies the active input dimensions and refines the most important ones. This criterion can be computed explicitly at a linear cost. Finally, we provide open-source codes for our full framework. We demonstrate the performance and scalability of the methodology in several synthetic examples with hundreds of dimensions under monotonicity constraints as well as on a real-world flood application.

Parameter identifiability of a deep feedforward ReLU neural network

The possibility for one to recover the parameters-weights and biases-of a neural network thanks to the knowledge of its function on a subset of the input space can be, depending on the situation, a curse or a blessing. On one hand, recovering the parameters allows for better adversarial attacks and could also disclose sensitive information from the dataset used to construct the network. On the other hand, if the parameters of a network can be recovered, it guarantees the user that the features in the latent spaces can be interpreted. It also provides foundations to obtain formal guarantees on the performances of the network. It is therefore important to characterize the networks whose parameters can be identified and those whose parameters cannot. In this article, we provide a set of conditions on a deep fully-connected feedforward ReLU neural network under which the parameters of the network are uniquely identified-modulo permutation and positive rescaling-from the function it implements on a subset of the input space.