Physics-informed, boundary-constrained Gaussian process regression for the reconstruction of fluid flow fields

Gaussian process regression techniques have been used in fluid mechanics for the reconstruction of flow fields from a reduction-of-dimension perspective. A main ingredient in this setting is the construction of adapted covariance functions, or kernels, to obtain such estimates. In this paper, we derive physics-informed kernels for simulating two-dimensional velocity fields of an incompressible (divergence-free) flow around aerodynamic profiles. These kernels allow to define Gaussian process priors satisfying the incompressibility condition and the prescribed boundary conditions along the profile in a continuous manner. Such physical and boundary constraints can be applied to any pre-defined scalar kernel in the proposed methodology, which is very general and can be implemented with high flexibility for a broad range of engineering applications. Its relevance and performances are illustrated by numerical simulations of flows around a cylinder and a NACA 0412 airfoil profile, for which no observation at the boundary is needed at all.

Non-asymptotic confidence regions on RKHS. The Paley-Wiener and standard Sobolev space cases

We consider the problem of constructing a global, probabilistic, and non-asymptotic confidence region for an unknown function observed on a random design. The unknown function is assumed to lie in a reproducing kernel Hilbert space (RKHS). We show that this construction can be reduced to accurately estimating the RKHS norm of the unknown function. Our analysis primarily focuses both on the Paley-Wiener and on the standard Sobolev space settings.

General reproducing properties in RKHS with application to derivative and integral operators

In this paper, we generalize the reproducing property in Reproducing Kernel Hilbert Spaces (RKHS). We establish a reproducing property for the closure of the class of combinations of composition operators under minimal conditions. As an application, we improve the existing sufficient conditions for the reproducing property to hold for the derivative operator, as well as for the existence of the mean embedding function. These results extend the scope of applicability of the representer theorem for regularized learning algorithms that involve data for function values, gradients, or any other operator from the considered class.

High-dimensional additive Gaussian processes under monotonicity constraints

We introduce an additive Gaussian process framework accounting for monotonicity constraints and scalable to high dimensions. Our contributions are threefold. First, we show that our framework enables to satisfy the constraints everywhere in the input space. We also show that more general componentwise linear inequality constraints can be handled similarly, such as componentwise convexity. Second, we propose the additive MaxMod algorithm for sequential dimension reduction. By sequentially maximizing a squared-norm criterion, MaxMod identifies the active input dimensions and refines the most important ones. This criterion can be computed explicitly at a linear cost. Finally, we provide open-source codes for our full framework. We demonstrate the performance and scalability of the methodology in several synthetic examples with hundreds of dimensions under monotonicity constraints as well as on a real-world flood application.

A comparison of mixed-variables Bayesian optimization approaches

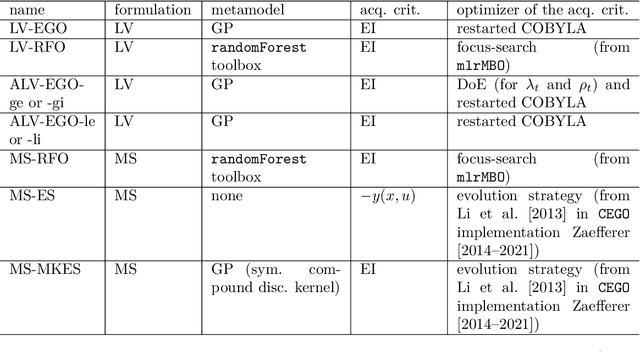
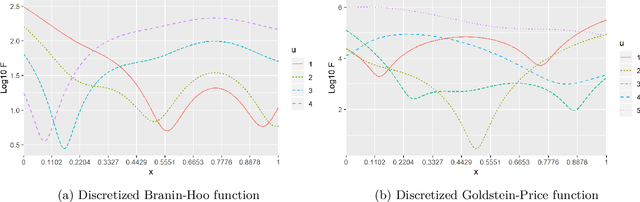
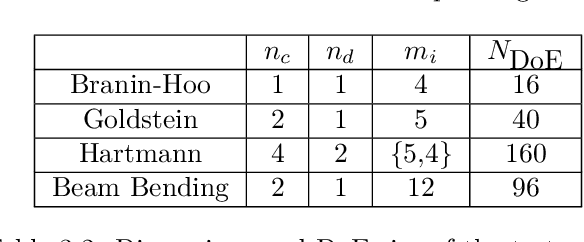
Most real optimization problems are defined over a mixed search space where the variables are both discrete and continuous. In engineering applications, the objective function is typically calculated with a numerically costly black-box simulation.General mixed and costly optimization problems are therefore of a great practical interest, yet their resolution remains in a large part an open scientific question. In this article, costly mixed problems are approached through Gaussian processes where the discrete variables are relaxed into continuous latent variables. The continuous space is more easily harvested by classical Bayesian optimization techniques than a mixed space would. Discrete variables are recovered either subsequently to the continuous optimization, or simultaneously with an additional continuous-discrete compatibility constraint that is handled with augmented Lagrangians. Several possible implementations of such Bayesian mixed optimizers are compared. In particular, the reformulation of the problem with continuous latent variables is put in competition with searches working directly in the mixed space. Among the algorithms involving latent variables and an augmented Lagrangian, a particular attention is devoted to the Lagrange multipliers for which a local and a global estimation techniques are studied. The comparisons are based on the repeated optimization of three analytical functions and a beam design problem.

Approximating Gaussian Process Emulators with Linear Inequality Constraints and Noisy Observations via MC and MCMC

Adding inequality constraints (e.g. boundedness, monotonicity, convexity) into Gaussian processes (GPs) can lead to more realistic stochastic emulators. Due to the truncated Gaussianity of the posterior, its distribution has to be approximated. In this work, we consider Monte Carlo (MC) and Markov chain Monte Carlo (MCMC). However, strictly interpolating the observations may entail expensive computations due to highly restrictive sample spaces. Having (constrained) GP emulators when data are actually noisy is also of interest. We introduce a noise term for the relaxation of the interpolation conditions, and we develop the corresponding approximation of GP emulators under linear inequality constraints. We show with various toy examples that the performance of MC and MCMC samplers improves when considering noisy observations. Finally, on a 5D monotonic example, we show that our framework still provides high effective sample rates with reasonable running times.

On the choice of the low-dimensional domain for global optimization via random embeddings

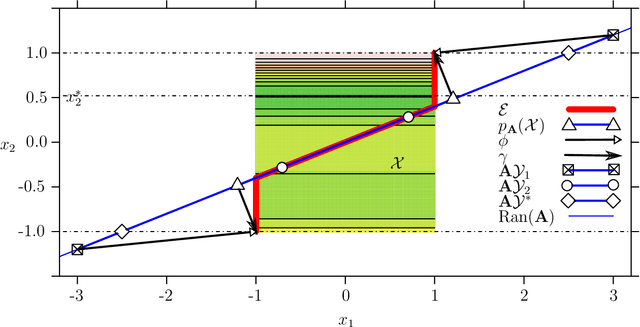
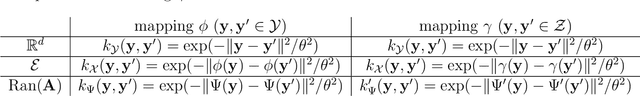
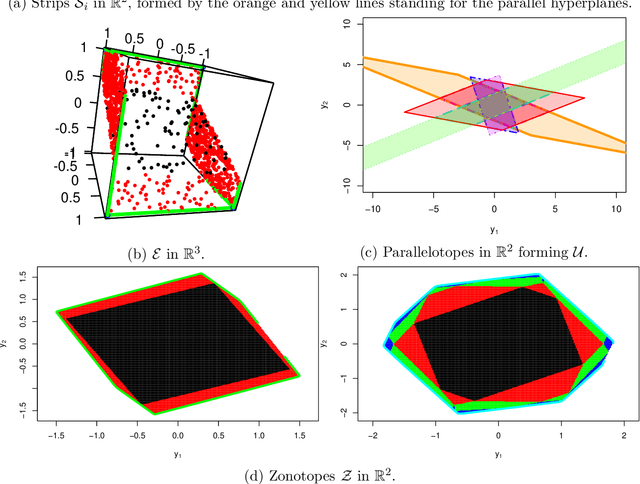
The challenge of taking many variables into account in optimization problems may be overcome under the hypothesis of low effective dimensionality. Then, the search of solutions can be reduced to the random embedding of a low dimensional space into the original one, resulting in a more manageable optimization problem. Specifically, in the case of time consuming black-box functions and when the budget of evaluations is severely limited, global optimization with random embeddings appears as a sound alternative to random search. Yet, in the case of box constraints on the native variables, defining suitable bounds on a low dimensional domain appears to be complex. Indeed, a small search domain does not guarantee to find a solution even under restrictive hypotheses about the function, while a larger one may slow down convergence dramatically. Here we tackle the issue of low-dimensional domain selection based on a detailed study of the properties of the random embedding, giving insight on the aforementioned difficulties. In particular, we describe a minimal low-dimensional set in correspondence with the embedded search space. We additionally show that an alternative equivalent embedding procedure yields simultaneously a simpler definition of the low-dimensional minimal set and better properties in practice. Finally, the performance and robustness gains of the proposed enhancements for Bayesian optimization are illustrated on numerical examples.

Finite-dimensional Gaussian approximation with linear inequality constraints

Introducing inequality constraints in Gaussian process (GP) models can lead to more realistic uncertainties in learning a great variety of real-world problems. We consider the finite-dimensional Gaussian approach from Maatouk and Bay (2017) which can satisfy inequality conditions everywhere (either boundedness, monotonicity or convexity). Our contributions are threefold. First, we extend their approach in order to deal with general sets of linear inequalities. Second, we explore several Markov Chain Monte Carlo (MCMC) techniques to approximate the posterior distribution. Third, we investigate theoretical and numerical properties of the constrained likelihood for covariance parameter estimation. According to experiments on both artificial and real data, our full framework together with a Hamiltonian Monte Carlo-based sampler provides efficient results on both data fitting and uncertainty quantification.

Poincaré inequalities on intervals -- application to sensitivity analysis

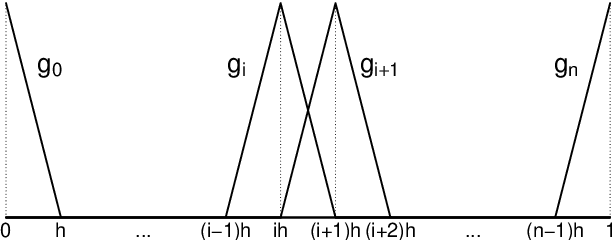
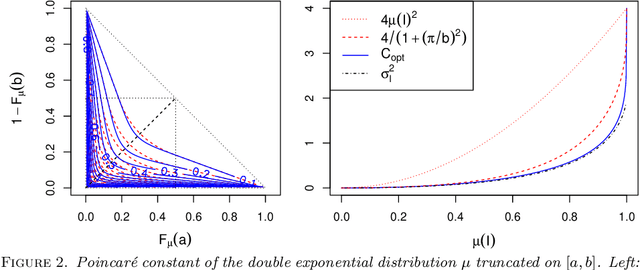
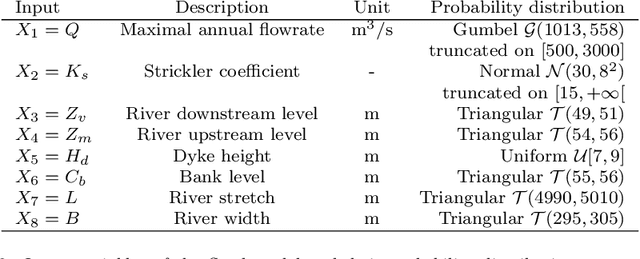
The development of global sensitivity analysis of numerical model outputs has recently raised new issues on 1-dimensional Poincar\'e inequalities. Typically two kind of sensitivity indices are linked by a Poincar\'e type inequality, which provide upper bounds of the most interpretable index by using the other one, cheaper to compute. This allows performing a low-cost screening of unessential variables. The efficiency of this screening then highly depends on the accuracy of the upper bounds in Poincar\'e inequalities. The novelty in the questions concern the wide range of probability distributions involved, which are often truncated on intervals. After providing an overview of the existing knowledge and techniques, we add some theory about Poincar\'e constants on intervals, with improvements for symmetric intervals. Then we exploit the spectral interpretation for computing exact value of Poincar\'e constants of any admissible distribution on a given interval. We give semi-analytical results for some frequent distributions (truncated exponential, triangular, truncated normal), and present a numerical method in the general case. Finally, an application is made to a hydrological problem, showing the benefits of the new results in Poincar\'e inequalities to sensitivity analysis.

A warped kernel improving robustness in Bayesian optimization via random embeddings

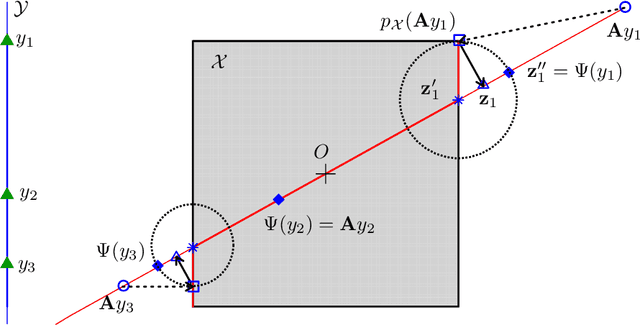
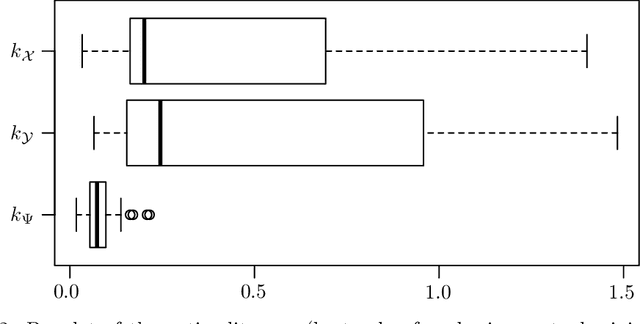
This works extends the Random Embedding Bayesian Optimization approach by integrating a warping of the high dimensional subspace within the covariance kernel. The proposed warping, that relies on elementary geometric considerations, allows mitigating the drawbacks of the high extrinsic dimensionality while avoiding the algorithm to evaluate points giving redundant information. It also alleviates constraints on bound selection for the embedded domain, thus improving the robustness, as illustrated with a test case with 25 variables and intrinsic dimension 6.