ANOVA kernels and RKHS of zero mean functions for model-based sensitivity analysis

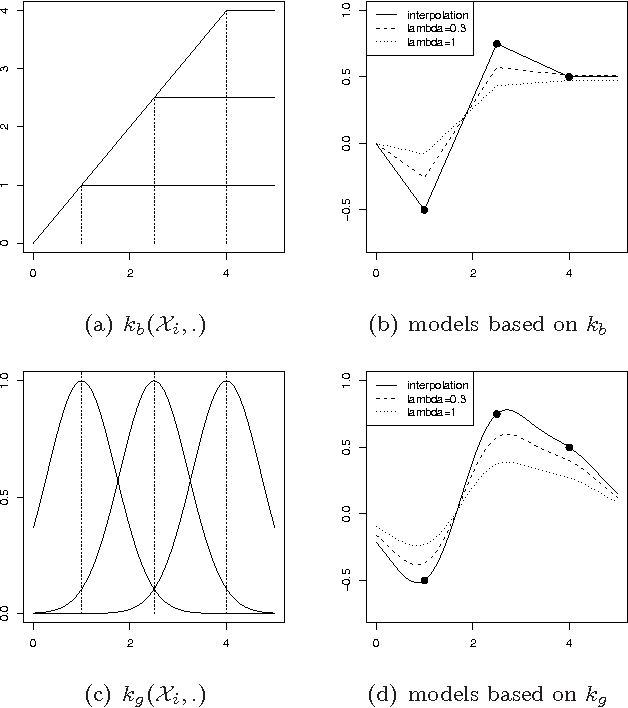
Given a reproducing kernel Hilbert space H of real-valued functions and a suitable measure mu over the source space D (subset of R), we decompose H as the sum of a subspace of centered functions for mu and its orthogonal in H. This decomposition leads to a special case of ANOVA kernels, for which the functional ANOVA representation of the best predictor can be elegantly derived, either in an interpolation or regularization framework. The proposed kernels appear to be particularly convenient for analyzing the e ffect of each (group of) variable(s) and computing sensitivity indices without recursivity.

Additive Covariance Kernels for High-Dimensional Gaussian Process Modeling

Gaussian process models -also called Kriging models- are often used as mathematical approximations of expensive experiments. However, the number of observation required for building an emulator becomes unrealistic when using classical covariance kernels when the dimension of input increases. In oder to get round the curse of dimensionality, a popular approach is to consider simplified models such as additive models. The ambition of the present work is to give an insight into covariance kernels that are well suited for building additive Kriging models and to describe some properties of the resulting models.

A Radar-Shaped Statistic for Testing and Visualizing Uniformity Properties in Computer Experiments

In the study of computer codes, filling space as uniformly as possible is important to describe the complexity of the investigated phenomenon. However, this property is not conserved by reducing the dimension. Some numeric experiment designs are conceived in this sense as Latin hypercubes or orthogonal arrays, but they consider only the projections onto the axes or the coordinate planes. In this article we introduce a statistic which allows studying the good distribution of points according to all 1-dimensional projections. By angularly scanning the domain, we obtain a radar type representation, allowing the uniformity defects of a design to be identified with respect to its projections onto straight lines. The advantages of this new tool are demonstrated on usual examples of space-filling designs (SFD) and a global statistic independent of the angle of rotation is studied.