Efficient pooling of predictions via kernel embeddings

Probabilistic predictions are probability distributions over the set of possible outcomes. Such predictions quantify the uncertainty in the outcome, making them essential for effective decision making. By combining multiple predictions, the information sources used to generate the predictions are pooled, often resulting in a more informative forecast. Probabilistic predictions are typically combined by linearly pooling the individual predictive distributions; this encompasses several ensemble learning techniques, for example. The weights assigned to each prediction can be estimated based on their past performance, allowing more accurate predictions to receive a higher weight. This can be achieved by finding the weights that optimise a proper scoring rule over some training data. By embedding predictions into a Reproducing Kernel Hilbert Space (RKHS), we illustrate that estimating the linear pool weights that optimise kernel-based scoring rules is a convex quadratic optimisation problem. This permits an efficient implementation of the linear pool when optimally combining predictions on arbitrary outcome domains. This result also holds for other combination strategies, and we additionally study a flexible generalisation of the linear pool that overcomes some of its theoretical limitations, whilst allowing an efficient implementation within the RKHS framework. These approaches are compared in an application to operational wind speed forecasts, where this generalisation is found to offer substantial improvements upon the traditional linear pool.

Non-Sequential Ensemble Kalman Filtering using Distributed Arrays

This work introduces a new, distributed implementation of the Ensemble Kalman Filter (EnKF) that allows for non-sequential assimilation of large datasets in high-dimensional problems. The traditional EnKF algorithm is computationally intensive and exhibits difficulties in applications requiring interaction with the background covariance matrix, prompting the use of methods like sequential assimilation which can introduce unwanted consequences, such as dependency on observation ordering. Our implementation leverages recent advancements in distributed computing to enable the construction and use of the full model error covariance matrix in distributed memory, allowing for single-batch assimilation of all observations and eliminating order dependencies. Comparative performance assessments, involving both synthetic and real-world paleoclimatic reconstruction applications, indicate that the new, non-sequential implementation outperforms the traditional, sequential one.

Consistency of some sequential experimental design strategies for excursion set estimation based on vector-valued Gaussian processes

We tackle the extension to the vector-valued case of consistency results for Stepwise Uncertainty Reduction sequential experimental design strategies established in [Bect et al., A supermartingale approach to Gaussian process based sequential design of experiments, Bernoulli 25, 2019]. This lead us in the first place to clarify, assuming a compact index set, how the connection between continuous Gaussian processes and Gaussian measures on the Banach space of continuous functions carries over to vector-valued settings. From there, a number of concepts and properties from the aforementioned paper can be readily extended. However, vector-valued settings do complicate things for some results, mainly due to the lack of continuity for the pseudo-inverse mapping that affects the conditional mean and covariance function given finitely many pointwise observations. We apply obtained results to the Integrated Bernoulli Variance and the Expected Measure Variance uncertainty functionals employed in [Fossum et al., Learning excursion sets of vector-valued Gaussian random fields for autonomous ocean sampling, The Annals of Applied Statistics 15, 2021] for the estimation for excursion sets of vector-valued functions.

Characteristic kernels on Hilbert spaces, Banach spaces, and on sets of measures

We present new classes of positive definite kernels on non-standard spaces that are integrally strictly positive definite or characteristic. In particular, we discuss radial kernels on separable Hilbert spaces, and introduce broad classes of kernels on Banach spaces and on metric spaces of strong negative type. The general results are used to give explicit classes of kernels on separable $L^p$ spaces and on sets of measures.

Uncertainty Quantification and Experimental Design for large-scale linear Inverse Problems under Gaussian Process Priors

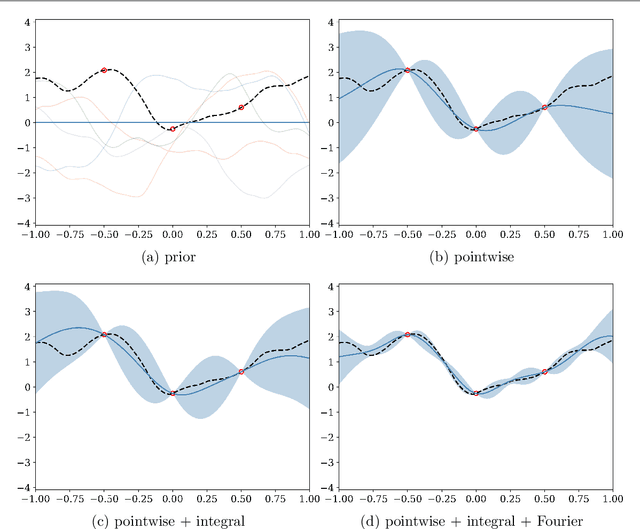
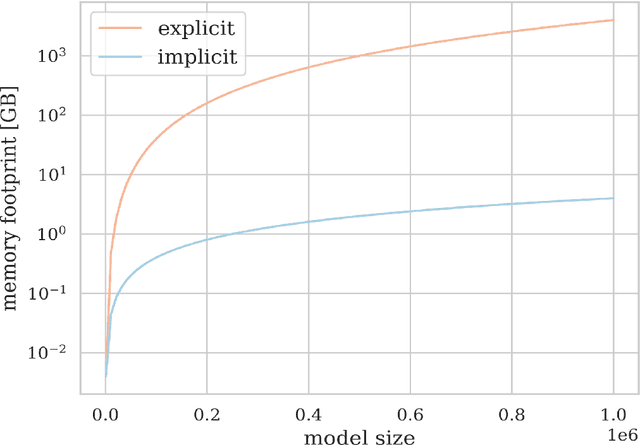
We consider the use of Gaussian process (GP) priors for solving inverse problems in a Bayesian framework. As is well known, the computational complexity of GPs scales cubically in the number of datapoints. We here show that in the context of inverse problems involving integral operators, one faces additional difficulties that hinder inversion on large grids. Furthermore, in that context, covariance matrices can become too large to be stored. By leveraging results about sequential disintegrations of Gaussian measures, we are able to introduce an implicit representation of posterior covariance matrices that reduces the memory footprint by only storing low rank intermediate matrices, while allowing individual elements to be accessed on-the-fly without needing to build full posterior covariance matrices. Moreover, it allows for fast sequential inclusion of new observations. These features are crucial when considering sequential experimental design tasks. We demonstrate our approach by computing sequential data collection plans for excursion set recovery for a gravimetric inverse problem, where the goal is to provide fine resolution estimates of high density regions inside the Stromboli volcano, Italy. Sequential data collection plans are computed by extending the weighted integrated variance reduction (wIVR) criterion to inverse problems. Our results show that this criterion is able to significantly reduce the uncertainty on the excursion volume, reaching close to minimal levels of residual uncertainty. Overall, our techniques allow the advantages of probabilistic models to be brought to bear on large-scale inverse problems arising in the natural sciences.

Fast ABC with joint generative modelling and subset simulation

We propose a novel approach for solving inverse-problems with high-dimensional inputs and an expensive forward mapping. It leverages joint deep generative modelling to transfer the original problem spaces to a lower dimensional latent space. By jointly modelling input and output variables and endowing the latent with a prior distribution, the fitted probabilistic model indirectly gives access to the approximate conditional distributions of interest. Since model error and observational noise with unknown distributions are common in practice, we resort to likelihood-free inference with Approximate Bayesian Computation (ABC). Our method calls on ABC by Subset Simulation to explore the regions of the latent space with dissimilarities between generated and observed outputs below prescribed thresholds. We diagnose the diversity of approximate posterior solutions by monitoring the probability content of these regions as a function of the threshold. We further analyze the curvature of the resulting diagnostic curve to propose an adequate ABC threshold. When applied to a cross-borehole tomography example from geophysics, our approach delivers promising performance without using prior knowledge of the forward nor of the noise distribution.

Goal-oriented adaptive sampling under random field modelling of response probability distributions

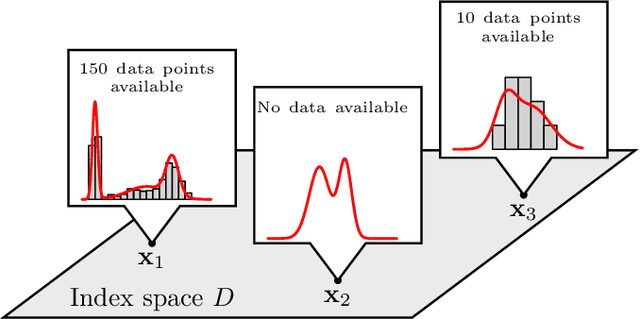
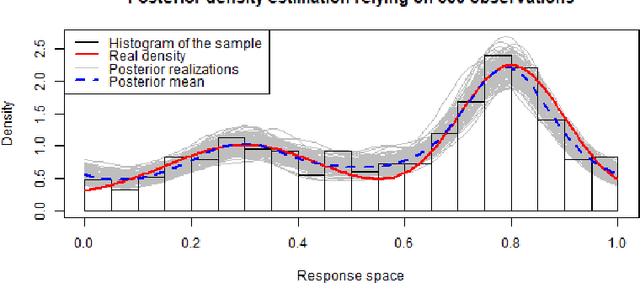
In the study of natural and artificial complex systems, responses that are not completely determined by the considered decision variables are commonly modelled probabilistically, resulting in response distributions varying across decision space. We consider cases where the spatial variation of these response distributions does not only concern their mean and/or variance but also other features including for instance shape or uni-modality versus multi-modality. Our contributions build upon a non-parametric Bayesian approach to modelling the thereby induced fields of probability distributions, and in particular to a spatial extension of the logistic Gaussian model. The considered models deliver probabilistic predictions of response distributions at candidate points, allowing for instance to perform (approximate) posterior simulations of probability density functions, to jointly predict multiple moments and other functionals of target distributions, as well as to quantify the impact of collecting new samples on the state of knowledge of the distribution field of interest. In particular, we introduce adaptive sampling strategies leveraging the potential of the considered random distribution field models to guide system evaluations in a goal-oriented way, with a view towards parsimoniously addressing calibration and related problems from non-linear (stochastic) inversion and global optimisation.

Fast calculation of Gaussian Process multiple-fold cross-validation residuals and their covariances

We generalize fast Gaussian process leave-one-out formulae to multiple-fold cross-validation, highlighting in turn in broad settings the covariance structure of cross-validation residuals. The employed approach, that relies on block matrix inversion via Schur complements, is applied to both Simple and Universal Kriging frameworks. We illustrate how resulting covariances affect model diagnostics and how to properly transform residuals in the first place. Beyond that, we examine how accounting for dependency between such residuals affect cross-validation-based estimation of the scale parameter. It is found in two distinct cases, namely in scale estimation and in broader covariance parameter estimation via pseudo-likelihood, that correcting for covariances between cross-validation residuals leads back to maximum likelihood estimation or to an original variation thereof. The proposed fast calculation of Gaussian Process multiple-fold cross-validation residuals is implemented and benchmarked against a naive implementation, all in R language. Numerical experiments highlight the accuracy of our approach as well as the substantial speed-ups that it enables. It is noticeable however, as supported by a discussion on the main drivers of computational costs and by a dedicated numerical benchmark, that speed-ups steeply decline as the number of folds (say, all sharing the same size) decreases. Overall, our results enable fast multiple-fold cross-validation, have direct consequences in GP model diagnostics, and pave the way to future work on hyperparameter fitting as well as on the promising field of goal-oriented fold design.

Learning excursion sets of vector-valued Gaussian random fields for autonomous ocean sampling

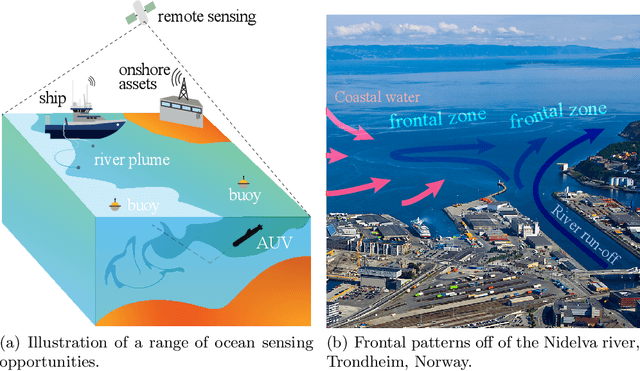
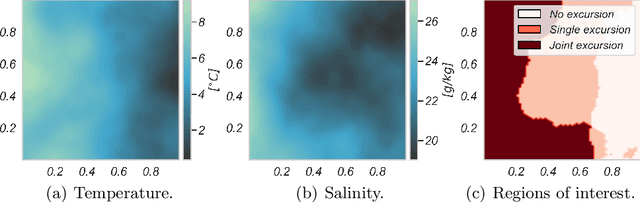
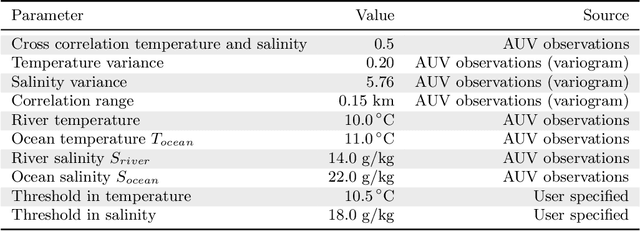
Improving and optimizing oceanographic sampling is a crucial task for marine science and maritime resource management. Faced with limited resources in understanding processes in the water-column, the combination of statistics and autonomous systems provide new opportunities for experimental design. In this work we develop efficient spatial sampling methods for characterizing regions defined by simultaneous exceedances above prescribed thresholds of several responses, with an application focus on mapping coastal ocean phenomena based on temperature and salinity measurements. Specifically, we define a design criterion based on uncertainty in the excursions of vector-valued Gaussian random fields, and derive tractable expressions for the expected integrated Bernoulli variance reduction in such a framework. We demonstrate how this criterion can be used to prioritize sampling efforts at locations that are ambiguous, making exploration more effective. We use simulations to study and compare properties of the considered approaches, followed by results from field deployments with an autonomous underwater vehicle as part of a study mapping the boundary of a river plume. The results demonstrate the potential of combining statistical methods and robotic platforms to effectively inform and execute data-driven environmental sampling.

Learning from demonstration with model-based Gaussian process

In learning from demonstrations, it is often desirable to adapt the behavior of the robot as a function of the variability retrieved from human demonstrations and the (un)certainty encoded in different parts of the task. In this paper, we propose a novel multi-output Gaussian process (MOGP) based on Gaussian mixture regression (GMR). The proposed approach encapsulates the variability retrieved from the demonstrations in the covariance of the MOGP. Leveraging the generative nature of GP models, our approach can efficiently modulate trajectories towards new start-, via- or end-points defined by the task. Our framework allows the robot to precisely track via-points while being compliant in regions of high variability. We illustrate the proposed approach in simulated examples and validate it in a real-robot experiment.