Optimal Control of Microswimmers for Trajectory Tracking Using Bayesian Optimization

Trajectory tracking for microswimmers remains a key challenge in microrobotics, where low-Reynolds-number dynamics make control design particularly complex. In this work, we formulate the trajectory tracking problem as an optimal control problem and solve it using a combination of B-spline parametrization with Bayesian optimization, allowing the treatment of high computational costs without requiring complex gradient computations. Applied to a flagellated magnetic swimmer, the proposed method reproduces a variety of target trajectories, including biologically inspired paths observed in experimental studies. We further evaluate the approach on a three-sphere swimmer model, demonstrating that it can adapt to and partially compensate for wall-induced hydrodynamic effects. The proposed optimization strategy can be applied consistently across models of different fidelity, from low-dimensional ODE-based models to high-fidelity PDE-based simulations, showing its robustness and generality. These results highlight the potential of Bayesian optimization as a versatile tool for optimal control strategies in microscale locomotion under complex fluid-structure interactions.

Modular Jump Gaussian Processes

Gaussian processes (GPs) furnish accurate nonlinear predictions with well-calibrated uncertainty. However, the typical GP setup has a built-in stationarity assumption, making it ill-suited for modeling data from processes with sudden changes, or "jumps" in the output variable. The "jump GP" (JGP) was developed for modeling data from such processes, combining local GPs and latent "level" variables under a joint inferential framework. But joint modeling can be fraught with difficulty. We aim to simplify by suggesting a more modular setup, eschewing joint inference but retaining the main JGP themes: (a) learning optimal neighborhood sizes that locally respect manifolds of discontinuity; and (b) a new cluster-based (latent) feature to capture regions of distinct output levels on both sides of the manifold. We show that each of (a) and (b) separately leads to dramatic improvements when modeling processes with jumps. In tandem (but without requiring joint inference) that benefit is compounded, as illustrated on real and synthetic benchmark examples from the recent literature.

Sensitivity Prewarping for Local Surrogate Modeling

In the continual effort to improve product quality and decrease operations costs, computational modeling is increasingly being deployed to determine feasibility of product designs or configurations. Surrogate modeling of these computer experiments via local models, which induce sparsity by only considering short range interactions, can tackle huge analyses of complicated input-output relationships. However, narrowing focus to local scale means that global trends must be re-learned over and over again. In this article, we propose a framework for incorporating information from a global sensitivity analysis into the surrogate model as an input rotation and rescaling preprocessing step. We discuss the relationship between several sensitivity analysis methods based on kernel regression before describing how they give rise to a transformation of the input variables. Specifically, we perform an input warping such that the "warped simulator" is equally sensitive to all input directions, freeing local models to focus on local dynamics. Numerical experiments on observational data and benchmark test functions, including a high-dimensional computer simulator from the automotive industry, provide empirical validation.

The Kalai-Smorodinski solution for many-objective Bayesian optimization

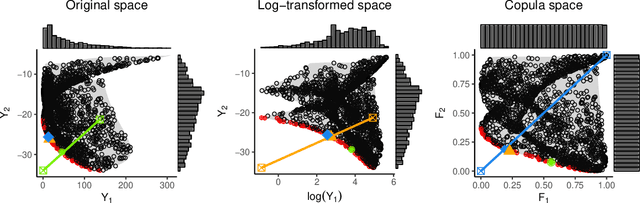
An ongoing aim of research in multiobjective Bayesian optimization is to extend its applicability to a large number of objectives. While coping with a limited budget of evaluations, recovering the set of optimal compromise solutions generally requires numerous observations and is less interpretable since this set tends to grow larger with the number of objectives. We thus propose to focus on a specific solution originating from game theory, the Kalai-Smorodinsky solution, which possesses attractive properties. In particular, it ensures equal marginal gains over all objectives. We further make it insensitive to a monotonic transformation of the objectives by considering the objectives in the copula space. A novel tailored algorithm is proposed to search for the solution, in the form of a Bayesian optimization algorithm: sequential sampling decisions are made based on acquisition functions that derive from an instrumental Gaussian process prior. Our approach is tested on three problems with respectively four, six, and ten objectives. The method is available in the package GPGame available on CRAN at https://cran.r-project.org/package=GPGame.

On the choice of the low-dimensional domain for global optimization via random embeddings

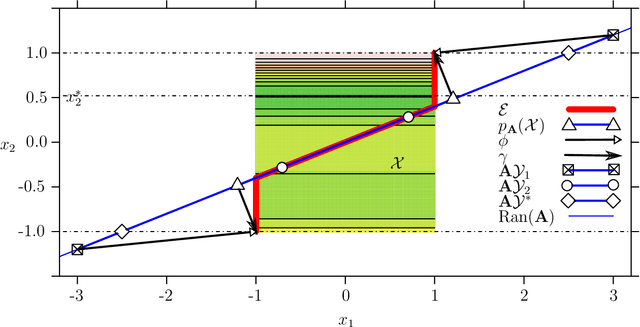
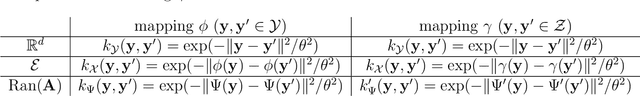
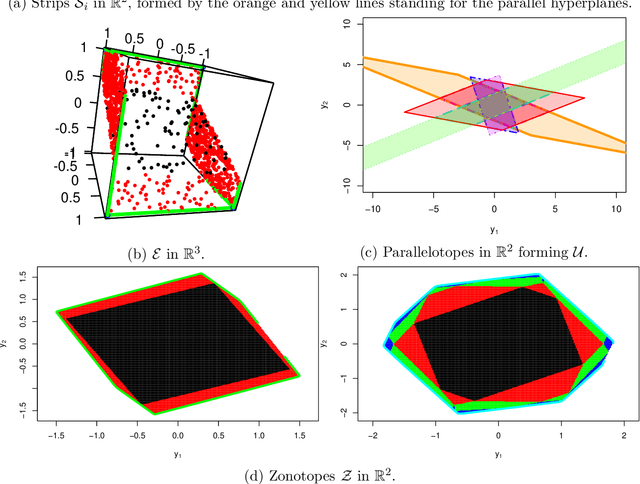
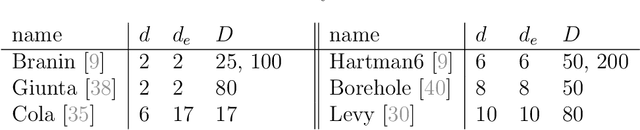
The challenge of taking many variables into account in optimization problems may be overcome under the hypothesis of low effective dimensionality. Then, the search of solutions can be reduced to the random embedding of a low dimensional space into the original one, resulting in a more manageable optimization problem. Specifically, in the case of time consuming black-box functions and when the budget of evaluations is severely limited, global optimization with random embeddings appears as a sound alternative to random search. Yet, in the case of box constraints on the native variables, defining suitable bounds on a low dimensional domain appears to be complex. Indeed, a small search domain does not guarantee to find a solution even under restrictive hypotheses about the function, while a larger one may slow down convergence dramatically. Here we tackle the issue of low-dimensional domain selection based on a detailed study of the properties of the random embedding, giving insight on the aforementioned difficulties. In particular, we describe a minimal low-dimensional set in correspondence with the embedded search space. We additionally show that an alternative equivalent embedding procedure yields simultaneously a simpler definition of the low-dimensional minimal set and better properties in practice. Finally, the performance and robustness gains of the proposed enhancements for Bayesian optimization are illustrated on numerical examples.

A warped kernel improving robustness in Bayesian optimization via random embeddings

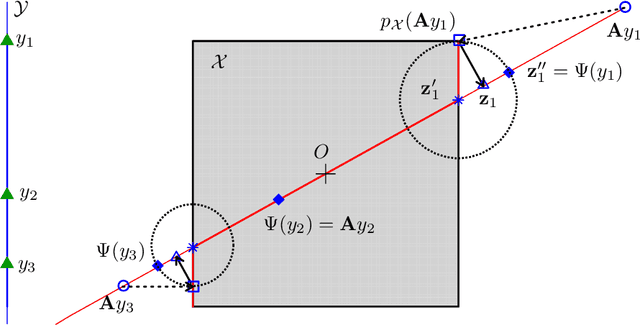
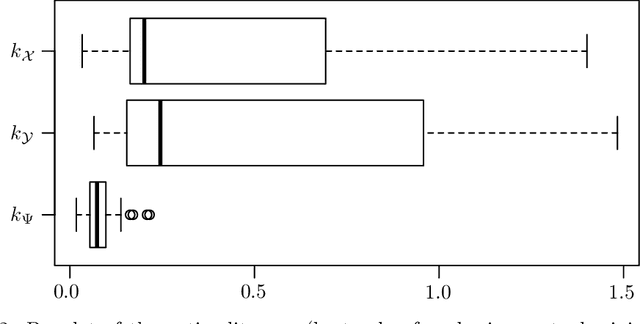
This works extends the Random Embedding Bayesian Optimization approach by integrating a warping of the high dimensional subspace within the covariance kernel. The proposed warping, that relies on elementary geometric considerations, allows mitigating the drawbacks of the high extrinsic dimensionality while avoiding the algorithm to evaluate points giving redundant information. It also alleviates constraints on bound selection for the embedded domain, thus improving the robustness, as illustrated with a test case with 25 variables and intrinsic dimension 6.